【算法】并查集
并查集基础:
查找、路径压缩、合并
int fa[maxn]; int find(int x){ if(fa[x] == x) return x; else return fa[x] = find(fa[x]); } void union(int x, int y){ fa[find(x)] = find(y); }
带权并查集:
查找+路径压缩:
递归向上查找父亲,向下计算权值
int find(int x){ if(fa[x] == x) return x; else{ int tmp = fa[x]; fa[x] = find(fa[x]); val[x] += val[tmp]; return fa[x]; } }
合并:
// x, y 之间建立权为d的父亲边 fx = find(x); fy = find(y); if(fx != fy){ fa[fx] = fy; val[fx] = -val[x] + val[y] + d; } // 验证 x,y 之间的权值是否为 d else{ if(val[x] - val[y] != d){ cnt++; // 不符合要求的个数 } }
例题:
经典带权并查集:HDU3038
题目大意:
现给出n个数字组成的序列,编号为1~n; 给出m个查询,每个查询的答案由a,b,s三个数组成,表示从第a个数加到第b个数的和为s; 但是其中有一些是有矛盾的(或者说错误的),求错误的查询答案有多少个。
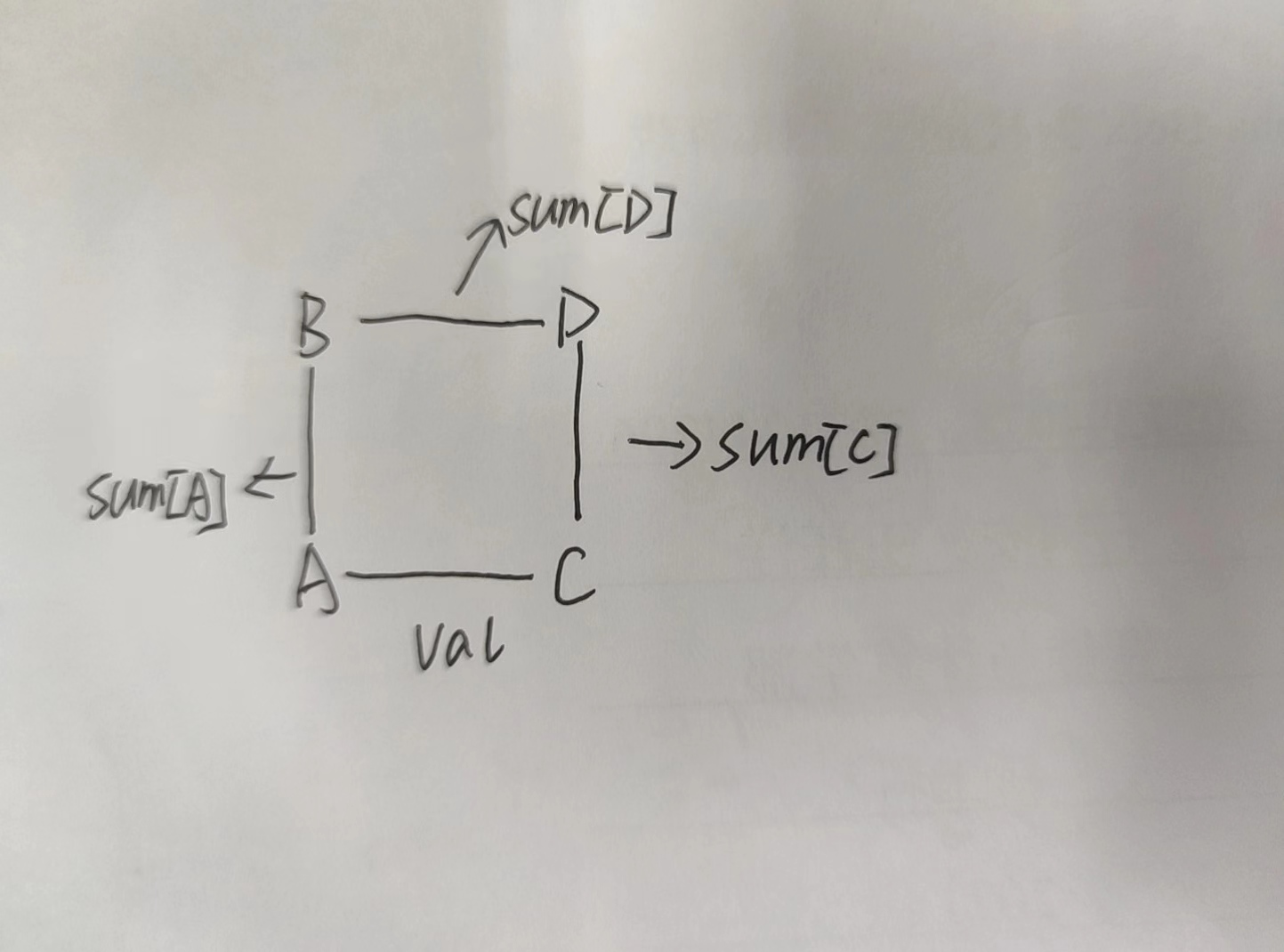
if(sum[A] - sum[C] != val) cnt++;
A、B 与 C、D 两个集合连接起来,即合并
fa[D] = B; sum[D]=sum[A]+val-sum[C];
AC代码:
#include<bits/stdc++.h> #define ll long long #define db double #define PII pair<int, int> using namespace std; const ll maxn = 2e5 + 10; int fa[maxn], sum[maxn]; int find(int i){ if(fa[i] == i) return i; int tmp = fa[i]; fa[i] = find(fa[i]); sum[i] += sum[tmp]; // 路径压缩,并且需要所有上面节点的值,与普通并查集不一样的点 return fa[i]; } int main(){ int n, m; while(scanf("%d%d", &n, &m) != EOF){ int ans = 0; for(int i = 0; i <= n; i++){ fa[i] = i; sum[i] = 0; } for(int i = 0; i < m; i++){ int a, b, s; scanf("%d%d%d", &a, &b, &s); a--; int aa = find(a); int bb = find(b); if(aa != bb){ fa[bb] = aa; sum[bb] = sum[a] + s - sum[b]; } else{ if(sum[b] - sum[a] != s) ans++; } } printf("%d\n", ans); } return 0; }
本文作者:shikean@Tianjin University
本文链接:https://www.cnblogs.com/keanshi/p/17572418.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。


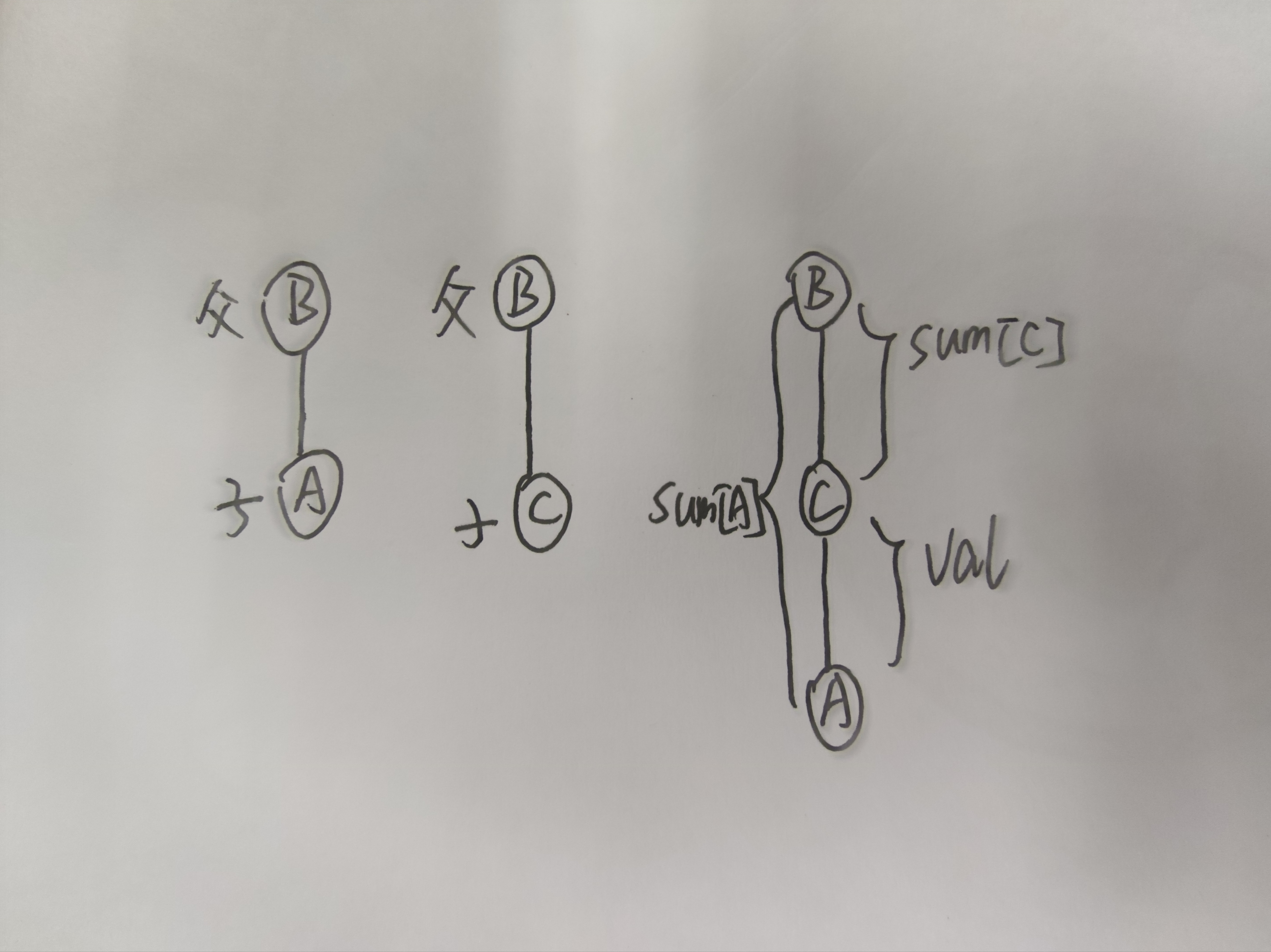



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步