tarjan无向图
无向图的割点与桥
定义
割点:删去这个点,图分裂成两个及以上不相连的子图。
桥(割边):删去这个边,图分裂成两个及以上不相连的子图。
需要说明的是,Tarjan算法从图的任意顶点进行DFS都可以得出割点集和割边集。
割点与桥的关系:
1)有割点不一定有桥,有桥一定存在割点
2)桥一定是割点依附的边。
桥的判定方法
搜索树上存在 \(x\) 的一个子节点 \(y\) 满足 $dfn[x] < low[y] \(; 从\)y\(出发,在不经过\)(x,y)$的前提下,永远无法到达 \(x\)或比\(x\)更早访问的点,所以 \((x,y)\)是割边
代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
inline int read() {
int x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x;
}
const int N=5005;
int n,m,root;
int hd[N<<1],nxt[N<<1],to[N<<1],tot=1;//初值
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
bool bridge[N];
int low[N],dfn[N],dfn_cnt;
void tarjan(int x,int edge) {//注意这里存的是边的编号
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y,i);
low[x]=min(low[x],low[y]);
if(low[y]>dfn[x]) bridge[i]=bridge[i^1]=1;
}
else if(i!=(edge^1)) low[x]=min(low[x],dfn[y]);
}
}
struct node{
int x,y;
bool operator < (const node &a) const {
return x==a.x?y<a.y:x<a.x;
}
}ans[N];
int main() {
n=read();m=read();
for(int i=1,x,y;i<=m;i++) {
x=read();y=read();
add(x,y),add(y,x);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
tarjan(i,0);
int cnt=0;
for(int i=2;i<=tot;i+=2)//从2开始
if(bridge[i]) ans[++cnt].x=min(to[i^1],to[i]),ans[cnt].y=max(to[i^1],to[i]);
sort(ans+1,ans+cnt+1);
for(int i=1;i<=cnt;i++)
printf("%d %d\n",ans[i].x,ans[i].y);
return 0;
}
割点
若 \(x\) 不是搜索树上根节点,存在$ x $的一个子节点 \(y\) 满足\(dfn[x] <= low[y]\) ;
注意无向图不需要\(vis[]\)判是否为返祖边,因为横叉边也能构成环
若 \(x\) 是根节点,则 \(x\)是割点 当且仅当搜索树上存在两个及以上 \(y\) 满足上述条件(因为显然肯定有一个)
#include <iostream>
#include <cstdio>
using namespace std;
inline int read(){
int x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x;
}
const int N=2e5+10;
int n,m;
struct edge{
int to,nxt;
}e[N];
int hd[N],tot;
inline void add(int x,int y){
e[++tot].to=y;e[tot].nxt=hd[x];hd[x]=tot;
}
int root;
int dfn[N],dfn_cnt,low[N];
int cut[N],ans=0;
void tarjan(int x){
int son=0;
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
if(x==root) son++;
if(x!=root&&low[y]>=dfn[x]) cut[x]=1;
}
low[x]=min(low[x],dfn[y]);
}
if(son>1) cut[x]=1;
}
int main(){
n=read();m=read();
for(int i=1,x,y;i<=m;i++){
x=read();y=read();
add(x,y);add(y,x);
}
for(int i=1;i<=n;i++)
if(!dfn[i])
root=i,tarjan(i);
for(int i=1;i<=n;i++)
if(cut[i]) ans++;
printf("%d\n",ans);
for(int i=1;i<=n;i++)
if(cut[i])
printf("%d ",i);
return 0;
}
BLO-Blockade
我们发现删掉一个割点 x 的话
$ ans= siz[s_1](n-siz[s_1]) + siz[s_2](n-siz[s_2]) +...+siz[s_k]*(n-siz[s_k])\+(n-1-\sum_{i=1}^{k}siz[i]) * (\sum_{i=1}^{k}siz[i])+1) + (n-1) $
三部分一个是路过x的个个连通块之间的,二是除了搜索树上的s_的连通块与others,最后是x到所有其他边
如果删掉的不是割点 $ ans=2*(n-1) $
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=100005;
const int M=500005;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m;
int hd[M<<1],nxt[M<<1],to[M<<1],tot=1;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int dfn[N],low[N],dfn_cnt,siz[N];
bool cut[N];
long long ans[N];
void tarjan(int x) {
dfn[x]=low[x]=++dfn_cnt;siz[x]=1;
int son=0,sum=0;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
siz[x]+=siz[y];
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]) {
son++;
ans[x]+=(long long)siz[y]*(n-siz[y]);
sum+=siz[y];
if(x!=1||son>1) cut[x]=1;
}
} else low[x]=min(low[x],dfn[y]);
}
if(cut[x]) ans[x]+=(long long)(n-sum-1)*(sum+1)+(n-1);
else ans[x]=2*(n-1);
}
int main() {
n=read();m=read();
for(int i=1,x,y;i<=m;i++) {
x=read();y=read();
add(x,y),add(y,x);
}
tarjan(1);
for(int i=1;i<=n;i++)
printf("%lld\n",ans[i]);
return 0;
}
[HNOI2012]矿场搭建
想贡献没想出来:
好吧正解貌似是分类讨论:
ans1+ ans2*
链: 2 1
环 2 C(siz,2)
叶子 1 num
割点后的联通块同叶子
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1000005;
inline int read() {
int x=0;char ch=getchar();
while(!isdigit(ch))ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x;
}
int hd[N],nxt[N],to[N],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int n,m,root;
int dfn[N],low[N],dfn_cnt;
int cut[N];
void tarjan(int x) {
int son=0;
dfn[x]=low[x]=++dfn_cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]) {
son++;
if(x!=root||son>1) cut[x]=1;
}
}else low[x]=min(low[x],dfn[y]);
}
if(son>1) cut[x]=1;
}
int siz,num,cut_cnt,vis[N];
void dfs(int x) {
vis[x]=num,siz++;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if((vis[y]!=num)&&cut[y]) cut_cnt++,vis[y]=num;
if(vis[y]) continue;
dfs(y);
}
}
long long ans1,ans2=1;
void clear() {
n=ans1=tot=siz=cut_cnt=num=0;ans2=1;//n忘了清零调了半天
memset(hd,0,sizeof(hd));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(vis,0,sizeof(vis));
memset(cut,0,sizeof(cut));
}
int main() {
int cas;
while(1) {
m=read();
if(!m) return 0;
for(int i=1,x,y;i<=m;i++) {
x=read(),y=read();
add(x,y),add(y,x);
n=max(n,max(x,y));
}
for(int i=1;i<=n;i++)
if(!dfn[i])
root=i,tarjan(i);
for(int i=1;i<=n;i++) {
if(!vis[i]&&!cut[i]) {
++num;
siz=cut_cnt=0;
dfs(i);
if(!cut_cnt) ans1+=2,ans2*=siz*(siz-1)/2;
if(cut_cnt==1) ans1+=1,ans2*=siz;
}
}
printf("Case %d: %lld %lld\n",++cas,ans1,ans2);
clear();
}
return 0;
}
CF1276B Two Fairs
显然 A,B 必须都是割点——保证必须经过A,B
然后A,B把原图分成三部分
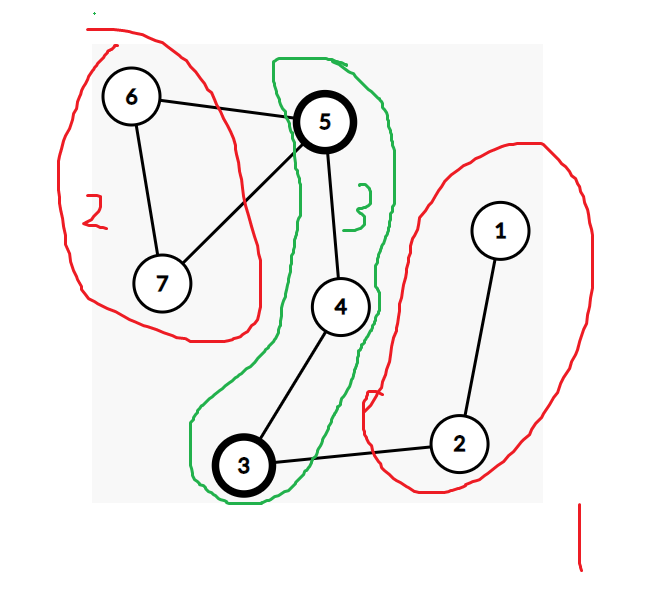
显然最后的答案就是 siz1 * siz2
具体实现:
我们以A的所有连边为出发点遍历,统计siz,但若搜到B,则这个贡献不要,B同理
注意,不要傻哈哈全memset,用多少清空多少
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N=5e5+10;
inline int read() {
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m,A,B;
int hd[N],to[N<<1],nxt[N<<1],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int dfn[N],low[N],cnt,root;
bool cut[N];
void tarjan(int x) {
int son=0;
dfn[x]=low[x]=++cnt;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(!dfn[y]) {
tarjan(y);
low[x]=min(low[x],low[y]);
if(x==root) son++;
if(x!=root&&dfn[x]<=low[y]) cut[x]=1;
}
low[x]=min(low[x],dfn[y]);
}
if(son>1) cut[x]=1;
}
int ans=0;
bool vis[N],flag=0;
int dfs(int x) {
if(x==A||x==B) flag=1;
vis[x]=1;
int size=1;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(vis[y]) continue;
size+=dfs(y);
}
return size;
}
int main() {
int T=read();
while(T--) {
for(int i=1;i<=n;i++) hd[i]=dfn[i]=low[i]=vis[i]=cut[i]=0;
tot=cnt=0;
n=read();m=read();A=read();B=read();
for(int i=1;i<=m;i++) {
int x=read(),y=read();
add(x,y);add(y,x);
}
root=1,tarjan(1);
if(!cut[A]||!cut[B]) {
puts("0");
continue;
}
int siza=0,sizb=0;
for(int i=1;i<=n;i++) vis[i]=0;
vis[A]=1;
for(int i=hd[A];i;i=nxt[i]) {
if(vis[to[i]]) continue;
flag=0;
ans=dfs(to[i]);
if(!flag) siza+=ans;
}
for(int i=1;i<=n;i++) vis[i]=0;
vis[B]=1;
for(int i=hd[B];i;i=nxt[i]) {
if(vis[to[i]]) continue;
flag=0;
ans=dfs(to[i]);
if(!flag) sizb+=ans;
}
printf("%lld\n",(long long)siza*sizb);
}
return 0;
}
无向图的双连通分量
没有割点的无向图称为点双连通图;没有割边的无向图称为边双连通图
在一个无向图中,点双连通的极大子图称为点双连通分量(v_DCC)
在一个无向图中,边双连通的极大子图称为边双连通分量(e_DCC)
点双连通图的定义等价于任意两条边都同在一个简单环中,而边双连通图的定义等价于任意一条边至少在一个简单环中。对一个无向图,点双连通的极大子图称为点双连通分量(简称双连通分量),边双连通的极大子图称为边双连通分量。
以下 3 条等价(均可作为点双连通图的定义):
(1)该连通图的任意两条边存在一个包含这两条边的简单环(不自交的环);
(2)该连通图没有割点;
(3)对于至少3个点的图,若任意两点有至少两条点不重复路径。
以下3 条等价(均可作为边双连通图的定义):
(1)该连通图的任意一条边存在一个包含这条边的简单环;
(2)该连通图没有桥;
(3)该连通图任意两点有至少两条边不重复路径。
边双e_DCC求法
删除所有的桥
代码(在求出所有桥的基础上)
void dfs(int x) {
col[x]=dcc;
for(int i=hd[x];i;i=e[i].nxt) {
int y=e[i].to;
if(col[y] || bridge[i]) continue;
dfs(y);
}
}
int main() {
for(int i=1;i<=n;i++)
if(!col[i])
dcc++,dfs(i);
}
边双缩点
Redundant Paths G
缩点就是 保留所有的桥边,其他的缩成一个点
上面那题ans=这个连通分量上的广义叶子节点(度数为1)除以2向上取整即为所需要加的边数。
证明:题目要求的是所有点至少度数为2,度数为1的点应该至少连一条边,最好的方法当然是一次性连两个度数为1的点,如果最后没有匹配(个数为奇数),仍然要连边,所以得出结论。
//边双桥的两端点
tot=1;
for(int i=2;i<=tot;i+=2)
if(bridge[i])
u=to[i],v=to[i^1];
有机化学之神偶尔会做作弊
边双缩点+树剖lca
点双 v_DCC求法
除了孤立点,点双大小至少为2
在求割点的时候维护一个栈,用vector 存起来
void tarjan(int x){
dfn[x]=low[x]=++dfn_cnt;
int son=0;
for(int i=hd[x];i;i=e[i].nxt){
int y=e[i].to;
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]){
son++;
if(x!=root || son>1) cut[x]=1;
cnt++;
do{
dcc[cnt].push_back(st[top--]);
}while(st[top+1]!=y)
dcc[cnt].push_back(x);
}
}else
low[x]=min(low[x],dfn[y]);
}
}
点双缩点
比边双缩点复杂一些——因为一个割点可能属于多个点双
我们给割点一个新编号,与包含它所有的点双连边。
bzoj 1123
poj 2942 ——bb402


 浙公网安备 33010602011771号
浙公网安备 33010602011771号