线段树优化建图

线段树优化建图

https://www.cnblogs.com/harryhqg/p/10456862.html

膜你赛T3path

适用情况

当点数很多，并且边集以区间形式 (点-->区间/区间->点) 给出

强行连边复杂度太大，考虑如何维护同一个子区间的连边，使用线段树优化。

建图思想

点向区间连边，可以向下传递；

假如：8 号点要向区间 [2,5] 连边，最后会是蓝边的样子（边权就省略了）：

那么区间向点连边呢？

反向再建一棵树。显然叶节点是相同的，所以两棵树会共用叶节点。

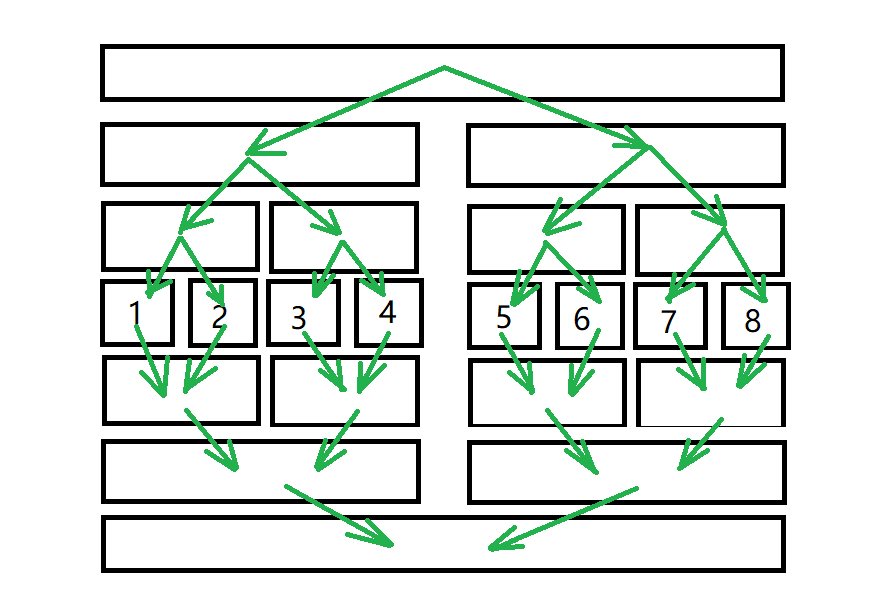
倒着的树上传递关系就变为，一个节点连了出边，那么他所代表的区间里所有节点都向外连了一条出边。

这些绿色的边的边权都是0 。

总结：

1.建立两个动态开点线段树，一个是入树，一个是出树

树上节点“权值”即为 p ——区间

入树：儿子向父亲连边权为0的边，出树：父亲向儿子连边权为0的边（很好理解，入树是要去出树的，所以往上走肯定是0，同理，出树向下是0）

2.连边：

首先两棵树的叶子结点连双向边，边权为0

\(u->[l,r]\) 出树上连边

\([l,r]->u\) 入树上连边

Solution

我们对每一条信息都单独开出来一个转移节点，然后就变成了 区间--> 点和 点-->区间的问题了。

但是双向边不能共用一个转移节点。因为这样其实上在 \([l_1,r_1]\)内的每个点之间都连了一条长度为2 的边。

实际做的时候，对每一个单向边都开一个转移节点，然后出边边权都设为 0，入边边权都设为 1就可以了。

还有一个比较妙的方法，是出入边权都设为1 然后最短路的答案除以2 ，也是可以的。

最短路不用 dij ，双端bfs即可 (0扔前面，1扔后面)

my代码：

#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
inline int read() {
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return x*f; 
}
const int N=12000010;
int n,m,s,rt_in,rt_out,tot;
int ls[N],rs[N];
int in[N],out[N];
int hd[N],e_cnt;
struct node{
    int id,val;
    node(){}
    node(int a,int b):id(a),val(b){}
};
struct edge{
    int to,nxt,w;
    edge(){}
    edge(int a,int b,int c):to(a),nxt(b),w(c){}
}e[N];
inline void add(int x,int y,int z){
    e[++e_cnt]={y,hd[x],z};hd[x]=e_cnt;
}
inline void build_in(int l,int r,int &p){
    p=++tot;
    if(l==r){in[l]=p;return;}
    int mid=(l+r)>>1;
    build_in(l,mid,ls[p]);
    build_in(mid+1,r,rs[p]);
    add(ls[p],p,0);
    add(rs[p],p,0);
}
inline void build_out(int l,int r,int &p){
    p=++tot;
    if(l==r){out[l]=p;return;}
    int mid=(l+r)>>1;
    build_out(l,mid,ls[p]);
    build_out(mid+1,r,rs[p]);
    add(p,ls[p],0);
    add(p,rs[p],0);
}
inline void insert_in(int ql,int qr,int l,int r,int cur,int p){
    if(ql<=l&&r<=qr){add(p,cur,1);return;}
    int mid=(l+r)>>1;
    if(ql<=mid) insert_in(ql,qr,l,mid,cur,ls[p]);
    if(qr>mid) insert_in(ql,qr,mid+1,r,cur,rs[p]);
}
inline void insert_out(int ql,int qr,int l,int r,int cur,int p){
    if(ql<=l&&r<=qr){add(cur,p,1);return;}
    int mid=(l+r)>>1;
    if(ql<=mid) insert_out(ql,qr,l,mid,cur,ls[p]);
    if(qr>mid) insert_out(ql,qr,mid+1,r,cur,rs[p]);
}
int dis[N];
bool vis[N];
void work(){
    deque <node> q;
    memset(dis,0x3f,sizeof(dis));
    dis[in[s]]=0;q.push_front({in[s],0});
    while(!q.empty()){
        int x=q.front().id;q.pop_front();
        if(vis[x])continue;
        vis[x]=1;
        for(int i=hd[x];i;i=e[i].nxt){
            int y=e[i].to,z=e[i].w;
            if(dis[y]>dis[x]+z){
                dis[y]=dis[x]+z;
                if(!vis[y]){
                    if(!z) q.push_front({y,dis[y]});
                    else q.push_back({y,dis[y]});
                }
            }
        }
    }
}
int main(){
    n=read();m=read();s=read();
    build_in(1,n,rt_in);
    build_out(1,n,rt_out);
    for(int i=1;i<=n;i++) add(in[i],out[i],0),add(out[i],in[i],0);
    for(int i=1;i<=m;i++){
        int l1=read(),r1=read(),l2=read(),r2=read();
        tot++;insert_in(l1,r1,1,n,tot,rt_in),insert_out(l2,r2,1,n,tot,rt_out);
        tot++;insert_in(l2,r2,1,n,tot,rt_in),insert_out(l1,r1,1,n,tot,rt_out);
    }
    work();
    for(int i=1;i<=n;i++)
        printf("%d\n",dis[out[i]]/2);
    return 0;
}

hs_black更优秀做法https://www.luogu.com.cn/blog/hs-black/solution-p6348

Legacy

模板——有边权

#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
const int N=3000010;
inline int read() {
	int x=0;char ch=getchar();
	while(!isdigit(ch))ch=getchar();
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return x;
}
int n,m,s,in_rt,out_rt,tree_cnt;
int ls[N],rs[N],in[N],out[N];
int hd[N],to[N],nxt[N],w[N],tot;
inline void add(int x,int y,int z) {
	to[++tot]=y;w[tot]=z;nxt[tot]=hd[x];hd[x]=tot;
}
#define mid ((l+r)>>1)
void build_in(int l,int r,int &p) {
	p=++tree_cnt;
	if(l==r) {
		in[l]=p;return;
	}
	build_in(l,mid,ls[p]);
	build_in(mid+1,r,rs[p]);
	add(ls[p],p,0);add(rs[p],p,0);
}
void build_out(int l,int r,int &p) {
	p=++tree_cnt;
	if(l==r) {
		out[l]=p;return;
	}
	build_out(l,mid,ls[p]);
	build_out(mid+1,r,rs[p]);
	add(p,ls[p],0);add(p,rs[p],0);	
}
void upd_in(int l,int r,int L,int R,int pos,int v,int &p) {
	if(L<=l&&r<=R) {
		add(p,pos,v);return;
	}
	if(L<=mid) upd_in(l,mid,L,R,pos,v,ls[p]);
	if(R>mid) upd_in(mid+1,r,L,R,pos,v,rs[p]);
}
void upd_out(int l,int r,int L,int R,int pos,int v,int &p) {
	if(L<=l&&r<=R) {
		add(pos,p,v);return;
	}
	if(L<=mid) upd_out(l,mid,L,R,pos,v,ls[p]);
	if(R>mid) upd_out(mid+1,r,L,R,pos,v,rs[p]);
}
ll dis[N];
bool vis[N];
struct node{
	int u;ll val;
	node(){}
	node(int u_,ll val_):u(u_),val(val_){}
	bool operator < (const node &x) const {
		return val>x.val;
	}
};
priority_queue<node>Q;
void dij() {
	memset(dis,0x3f,sizeof(dis));
	s=in[s];
	dis[s]=0;
	Q.push(node(s,0));
	while(Q.size()) {
		int x=Q.top().u;Q.pop();
		if(vis[x]) continue;
		vis[x]=1;
		for(int i=hd[x];i;i=nxt[i]) {
			int y=to[i];
			if(dis[y]>dis[x]+w[i]) {
				dis[y]=dis[x]+w[i];
				Q.push(node(y,dis[y]));
			}
		}
	}
}
int main() {
	n=read();m=read();s=read();
	build_in(1,n,in_rt);
	build_out(1,n,out_rt);
	for(int i=1;i<=n;i++) 
		add(in[i],out[i],0),add(out[i],in[i],0);
	int op,l,r,x,v;
	while(m--) {
		op=read();
		if(op==1) {
			l=read();r=read();v=read();
			add(in[l],out[r],v);
		}
		if(op==2) {
			x=read();l=read();r=read();v=read();
			upd_out(1,n,l,r,in[x],v,out_rt);
		}
		if(op==3) {
			x=read();l=read();r=read();v=read();
			upd_in(1,n,l,r,out[x],v,in_rt);			
		}
	}
	dij();
	for(int i=1;i<=n;i++) 
		if(dis[out[i]]==dis[0]) printf("-1 ");
		else printf("%lld ",dis[out[i]]);
	return 0;
}