组合

四个基本计数原理

划分：集合S的一个划分是它的子集$S_1,S_2,S_3…S_m$ 使每个元素恰好只属于其中的一个子集。

加法原理：$|S| = |S_1| + |S_2| + |S_3| +...+|S_m|$

乘法原理 ：设$S$是有序对$(a,b)$的集合，对象$a$来自大小为$p$的集合，对象$b$来自大小为$q$的集合，则$|S|=p*q$

减法原理：设$A\subseteq U$,且 $\bar{A}=\complement_UA$ ，那么$|A|=|U|-|\bar{A|}$

除法原理: $k=\frac{|S|}{m}$，其中$m$为在一个部分中的对象数目。

加法原理

分类加法计数

每个事件的产生方式不重合

事件A有$p$种产生方式，事件B有$q$种产生方式，则“A或B”有$p+q$种

例：从家A到学校B的道路地图如右图，问每次只能向右或向下走，有多少种行走路线方案？

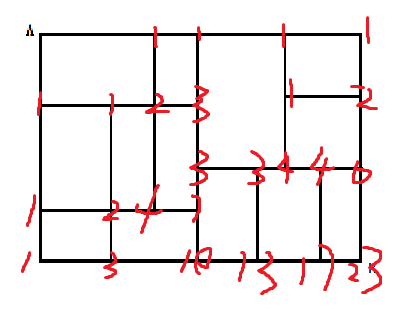
扩展：

一般化这个问题：从$n*m$ 棋盘左上角到右下角共有多少种走法，只能往右和往下走?

递推 :

$f[i][j]=f[i-1][j]+f[i][j-1]$

组合：

总共要向下$n-1$次，向右$m-1$次
所以方案数就是从$n-1+m-1$次中选出$n-1$向下，其余向右 $C_{n+m-2}^{~n-1}$

CF559C Gerald and Giant Chess

计数dp：

\[设f[i]表示从（1,1）到i方案数（不考虑黑点）\\那么答案其实就是总的方案数-不合法的方案数\\f_i=C_{x_i+y_i-2}^{x_i-1}-\sum_{j=1}^{i-1}C_{x_i+y_i-x_j-x_j}^{x_i-x_j}\\S把终点也看成黑点，那么答案就是f[n+1]咯\\ \]

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
const int N=2e5+10;
const int P=1e9+7;
typedef long long LL;
inline int read() {
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
	return f*x;
}
int n,m,k;
pair<int,int> p[N];
LL ans,dp[N],fac[N*2],inv[N*2];
LL qpow(LL a,LL b) {
	LL ans=1;
	while(b) {
		if(b&1) ans=ans*a%P;
		a=a*a%P;
		b>>=1;
	}
	return ans;
}
LL C(int n,int m) {
	if(n<0||m<0||n<m) return 0;
	return fac[n]*inv[n-m]%P*inv[m]%P;
}
int main() {
	n=read();m=read();k=read();
	for(int i=1;i<=k;i++)
		p[i].first=read(),p[i].second=read();
	p[++k]=make_pair(n,m);
	sort(p+1,p+1+k);
	
	fac[0]=1;
	for(int i=1;i<=200000;i++) fac[i]=fac[i-1]*i%P;
	inv[200000]=qpow(fac[200000],P-2);
	for(int i=200000;i>=0;i--) inv[i-1]=inv[i]*i%P;
	
	dp[1]=C(p[1].first+p[1].second-2,p[1].first-1);
	for(int i=2;i<=k;i++) {
		dp[i]=C(p[i].first+p[i].second-2,p[i].first-1);
		for(int j=1;j<i;j++) {
			if(p[j].first<=p[i].first&&p[j].second<=p[i].second) {
				dp[i]-=C(p[i].first-p[j].first+p[i].second-p[j].second,p[i].first-p[j].first)*dp[j]%P;
				dp[i]=(dp[i]+P)%P;
			}
		} 
	}
	printf("%lld\n",dp[k]);
	return 0;
}

乘法原理

分步乘法技术

事件A有p种产生方式，事件B有q种产生方式，则“A与B”有p*q种

例1：该学校有13门数学课，87门英语课，5门物理课可以选，某生想选一门数学课，一门英语课，两门物理课，有多少种方案？

根据乘法原理：answer=1387($C_5^2$)=11310(种)

例2：N个有编号结点的无向图有多少种(无重边自环)？其中有多少个图构成一个环？

$2^{n(n-1)/2}$

除法原理

一些简单题

例1：将左图五块分别用红绿蓝三种颜色染，相邻的块颜色必须不同，有多少种不同的染色方法？如果用红绿蓝黄四种颜色呢？

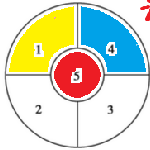
三种：中心颜色有三种，边上的可以上下颠倒（2种），一共是3*2=6

　四种： ⑤染4种颜色皆可（假设为红），①可染3种颜色（黄），④可染2种颜色（蓝），而对于③，染绿色和黄色是不等价的，这里用加法原理

　若染黄色，2有两种可能（绿、蓝）；若染绿色，2只有一种可能（蓝）

一共$（）4*3*2*（1+2）=72$

例2

A,B,C,D,E,F,G七人排成一排照相，要求：①A要么在最左侧，要么在最右侧②B,C二人必须相邻③A不能与E和F相邻④F,G二人必须相邻，问方案数

A在左右无差别（假设在左），A_ _ _ _ _ _， BC相邻有两种（BC or CB）无差别，可以看为一个人X, FG必须相邻，而顺序有差别（因为A不能与F相邻）

用加法原理两种情况（1）FG X E D (FG、E)不能挨着A 共$2*3*2*1$种（2）GF X E D 共$ 332*1$

$sum=2*2*(2*3*2*1+3*3*2*1)=120$

例3：

一个8×8的棋盘上有多少种放置4个棋子的方法，使得每行每列最多只有一个棋子。

$C(8,4) * A(8,4)$

8行里选4行--> $C(8,4)$，然后在4行8列中放4个-->$A(8,4)$

BZOJ 2467

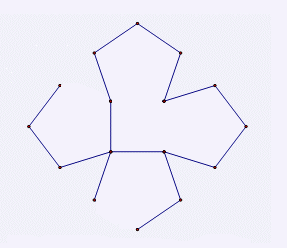
给定一个图，图的中心是一个n个点的多边形，每条边都外接一个五边形，求生成树个数。n<=100 (mod 2007)

考虑如果$n$个五边形每个断掉一条边就会得到一个基环外向树，此时还需要断掉一条边，这意味着n个五边形中就有一个五边形要断掉两条边，并且容易想到有一条必然是在中心的那个$n$边形上，那么就可以用组合数学来表示了。

　　从$n$个五边形中选取一个是选两条边的，这个五边形在中央$n$边形上那条边必选，那么只需在剩下4条边再断一条即可，而剩下的$n−1$个五边形都是随便断一条即可，

　　总方案数就是$4∗n∗5^(n−1)$。

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <string>
#include <complex>
#include <bitset>
using namespace std;
typedef long long LL;
typedef long double LB;
typedef complex<double> C;
const double pi = acos(-1);
const int mod = 2007;
int n,ans;
inline int getint(){
    int w=0,q=0; char c=getchar(); while((c<'0'||c>'9') && c!='-') c=getchar();
    if(c=='-') q=1,c=getchar(); while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar(); return q?-w:w;
}
inline int fast_pow(int x,int y){
    int r=1;
    while(y>0) {
        if(y&1) r*=x,r%=mod;
        x*=x; x%=mod;
        y>>=1;
    }
    return r;
}
inline void work(){
    int T=getint();
    while(T--) {
        n=getint(); ans=4*n;
        ans*=fast_pow(5,n-1);
        ans%=mod;
        cout<<ans<<endl;
    }
}
int main()
{
    work();
    return 0;
}

排列

组合

1.从$n$个不同元素中每次取出$m$个不同元素$（0≤m≤n）$，不管其顺序合成一组，称为从$n$个元素中不重复地选取$m$个元素的一个组合。所有这样的组合的总数称为组合数，这个组合数的计算公式为

$C_n^m= A_{n}^{m}/A_{m}^{m}=\frac{n!}{m!(n-m)!},C_n^0=1$

组合不考虑顺序
$A(n,m)$ 有 $A(m,m)$个同构，故 $C(n,m)=A(n,m)/A(m,m)$;

组合恒等式（组合数性质）

\[C(n,m)=C(n,n-m) ——中心对称\\∑C(n,i)=2^n ——每一行的和\\∑i*C(n,i)=n*2^{n-1} --结合二项式理解\\∑(i<=n)C(i,m)=C(n+1,m+1) ——折线\\∑(i<=k)C(n,i)*C(m,k-i)=C(n+m,k)\\ \]

吸收恒等式：

\[\binom n m=\frac{n!}{m!(n-m)!} = \frac{n}{m}\times\frac{(n-1)(n-2)\cdots(n-m+1)}{(m-1)(m-2)\cdots 1}\\\binom n m=\frac n m\binom {n-1}{m-1} \]

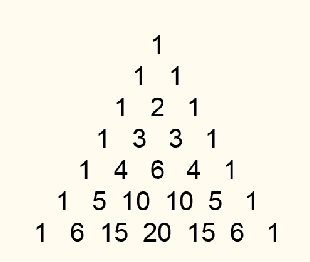
结合右下图杨辉三角理解

组合数代码实现

1.递推

	for(int i=0;i<=2000;i++)
		c[i][0]=c[i][i]=1;
	for(int i=1;i<=2000;i++)
		for(int j=1;j<i;j++)
			c[i][j]=(c[i-1][j-1]+c[i-1][j])%k;

2.逆元+快速幂

LL fac[N],inv[N];
LL qpow(LL a,LL b) {
	LL ans=1;
	while(b) {
		if(b&1) ans=ans*a%P;
		a=a*a%P;
		b>>=1;
	}
	return ans;
}
LL C(int n,int m) {
	return fac[n]*inv[n-m]%P*inv[m]%P;
}
fac[0]=1;
for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i%P;
inv[n]=qpow(fac[n],P-2);
for(int i=n;i;i--) inv[i-1]=inv[i]*i%P;

3.当n和m比较大而mod为素数且比较小(10^5左右)的时候，可以用Lucas定理计算

Lucas定理：

若p为质数，有

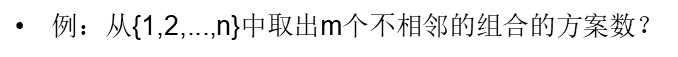
\[{n\choose m}\equiv {{n\mod p}\choose{m\mod p}}*{{n/p}\choose{m/p}} \]

戳这里

先放$m$个球，然后相邻两个球之间插$m-1$个球隔开，共用了$2m$个球

在$m+1$个空隙里，放$n-(2m+1)$个球，可空

整理得$C(n-m+1,m)$

帕斯卡三角

对于帕斯卡三角的第$n$行的第$m$个数，为组合数$C(n,m)$，由观察或加法原理推导得出组合数的递推式(帕斯卡公式)：
$C(n,m)=C(n-1,m-1)+C(n-1,m)$

二项式定理：

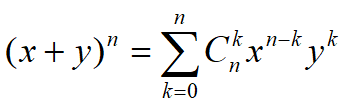
故组合数又称二项式系数。
代入$x=1,y=1$可得组合恒等式②
代入$x=1,y=-1$可得组合恒等式③

注意到，杨辉三角第n行第k列的数为$\binom n k$ 。

第n行的和为$2^{n}$

\[(x+1)^n=\sum^n_{i=0}x^i\binom n i \]

简单证明：

\[(x+1)^n=(x-1)\times(x-1)^{n-1} \]

考虑其组合意义，$(x+1)^n$ 的第k项就是用x乘上$(x-1)^{n-1}$的第k-1项加上1乘上$(x-1)^{n-1}$ 的第k-1项。那么就有

\[[x^k](x+1)^n=[x^{k-1}](x-1)^{n-1}+[x^k](x-1)^n \]

即$[x^k](x-1)^n=\binom n k$

二项式定理

由上式，我们有：

\[(x+1)^n=\sum^n_{i=0}x^i\binom n i \]

取$x=\frac a b$,有：

\[(\frac a b+1)^n=\sum^n_{i=0}\binom n ia^ib^{-i} \]

两边同乘$b^n$,得：

\[(a+b)^n=\sum^n_{i=0}\binom n ia^ib^{n-i} \]

二项式反演

咕咕咕

https://www.cnblogs.com/GXZlegend/p/11407185.html

https://247650.blog.luogu.org/er-xiang-shi-fan-yan

http://blog.miskcoo.com/2015/12/inversion-magic-binomial-inversion

https://www.cnblogs.com/hanyuweining/p/11950267.html

二.容斥原理和集合反演

2.1 容斥原理

\[|A\cup B \cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C| \]

这是最基础的集合容斥。

容斥定理

对于多个集合，我们有：

\[|\bigcup^n_{i=1}A_i|=\sum_{T\subseteq[1,n]}(-1)^{|T|-1}|\bigcap_{j\in T}S_j| \]

集合反演

对于函数$f(S),g(S)$，有

\[f(S)=\sum_{T\subseteq S}g(T)\Leftrightarrow g(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|} f(T) \]

证明，先咕着。

多重集合的排列

假设有$n_1$个$a_1$,$n_2$个$a_2$….$n_k$个$a_k$，将其全部排成一列，共有多少种方案。（无序）
先假设是有序的，那么就是全排列 $∑(n_k!)$
然后除法原理，除以等价类$π(n_k!)$
$Answer=(∑n_k!)/π(n_k!)$

题

排队

有$n$名男同学,$m$名女同学和两名老师要排队参加体检。他们排成一条直线，并且任意两名女同学不能相邻，两名老师也不能相邻，那么一共有多少种排法呢？（注意：任意两个人都是不同的）

第一种情况，老师女生男生间隔站
先男生全排列，方案数$A(n,n)$，产生$n+1$个空格
然后老师插空，方案数$A(n+1,2)$，此刻队列中共有$n+3$个空格
女生插空，方案数$A(n+3,m)$
那么第一种情况的方案数即为$A(n,n)*A(n+1,2)*A(n+3,m)$
第二种情况，两个老师一个女生看成一个男生
那么这个新的男生的方案数为$A(2,2)*m$
之后全排列，方案数$A(n+1,n+1)$，产生$n+2$个空格
其余女生插空，方案数$A(n+2,m-1)$
第二种情况的方案数即为$A(2,2)*m*A(n+1,n+1)*A(n+2,m-1)$
总共方案数为两种情况方案数相加

然后恶心的高精。。。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct BIG
{
    int a[12000],len;
    BIG(){memset(a,0,sizeof(a));len=0;}
}ans,cnt;
BIG mul(BIG n1,int x)
{
    BIG res;
    res.len=n1.len;
    for(int i=1;i<=n1.len;i++)res.a[i]=n1.a[i]*x;
    for(int i=1;i<=res.len;i++)
    {
        res.a[i+1]+=res.a[i]/10;
        res.a[i]%=10;
    }
    int i=res.len;
    while(res.a[i+1]>0)
    {
        i++;
        res.a[i+1]+=res.a[i]/10;
        res.a[i]%=10;
    }
    while(res.a[i]==0 && i>1)i--;
    res.len=i;
    return res;
}
BIG add(BIG n1,BIG n2)
{
    BIG res;
    res.len=max(n1.len,n2.len);
    for(int i=1;i<=res.len;i++)res.a[i]=n1.a[i]+n2.a[i];
    for(int i=1;i<=res.len;i++)
    {
        res.a[i+1]+=res.a[i]/10;
        res.a[i]%=10;
    }
    int i=res.len;
    while(res.a[i+1]>0)
    {
        i++;
        res.a[i+1]+=res.a[i]/10;
        res.a[i]%=10;
    }
    while(res.a[i]==0 && i>1)i--;
    res.len=i;
    return res;
}
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    if(n+3<m){printf("0\n");return 0;}
    //A(n,n)*A(n+1,2)*A(n+3,m)
    //n! * n * n+1 * n+3-m+1 ... n+3
    ans.a[1]=1;ans.len=1;
    for(int i=1;i<=n;i++)ans=mul(ans,i);
    for(int i=n;i<=n+1;i++)ans=mul(ans,i);
    for(int i=n+3-m+1;i<=n+3;i++)ans=mul(ans,i);
    //A(2,2)*m*A(n+1,n+1)*A(n+2,m-1)
    //2*m* n+1! * n+2-(m-1)+1...n+2    
    cnt.a[1]=2;cnt.len=1;
    for(int i=1;i<=n+1;i++)cnt=mul(cnt,i);
    for(int i=n+2-(m-1)+1;i<=n+2;i++)cnt=mul(cnt,i);
    cnt=mul(cnt,m);

    ans=add(ans,cnt);
    for(int i=ans.len;i>=1;i--)printf("%d",ans.a[i]);
    printf("\n");
    return 0;
}

bzoj2729

poj3252

bzoj3505

$C(n*m,3)$,然后减去三点共线的情况。
首先三点在一条水平或竖直的直线上非常好处理。直接减去$c(n)(3)*m+c(m)(3)*n$即可。
然后考虑斜着的情况。
我们枚举一下边上两个点的横坐标之差、纵坐标之差$(i,j)$
设线段上的点坐标$(i/t,j/t)$，这个点为整点，要想使这个点坐标最小，那么$t=gcd(i,j)$
线段段数$(i,j)/(i/gcd,j/gcd)==gcd(i,j)$
那么中间点可选的位置就是$gcd(i,j)-1$(线段数 + 1 =点数，两端不可选-2);
然后再乘上这种直线的条数即可。

bzoj2111

称一个1,2,...,N的排列P1,P2...,Pn是Magic的，当且仅当$2<=i<=N$时，$Pi>Pi/2$. 计算1，2，...N的排列中有多少是Magic的，答案可能很大，只能输出模P以后的值

求小根完全二叉树的个数

树上dp 定义设$f[i]$表示以$i$为根的子树的方案数，$s[i]$为子树大小,$ls=i<<1;rs=i<<1 | 1$
$f[n]=f[ls] * f[rs] * C(s[i] - 1 , s[ls] )$

可以知道，$n$可以从后向前递推。

#include<iostream> 
#include<cstdio> 
using namespace std;
#define ll long long
#define ls (i<<1)
#define rs (i<<1|1)//一定记得加括号！！！！ 
const int N = 5e6+5;
int n,p;
ll a[N],f[N],s[N],inv[N];
ll qpow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1)ans=(ans*a)%p;
        b>>=1;
        a=(a*a)%p;
    }
    return (ans+p)%p;
}
ll C(ll n,ll m){
    if(n<m)return 0;
    return (a[n]*inv[m]%p)*inv[n-m]%p;
}
ll lucas(ll n,ll m){
    if(!n && !m)return 1;
    return C(n%p,m%p)*lucas(n/p,m/p)%p;
}
int main(){
    scanf("%d%d",&n,&p) ;
    a[0]=1;inv[0]=1;inv[1]=1;
    for(int i=1;i<=n;i++)a[i]=(a[i-1]*i)%p;
    for(int i=2;i<=n;i++)inv[i]=qpow(a[i],p-2);
    for(int i=n;i;i--){
        s[i]=s[ls]+s[rs]+1;
        f[i]=lucas(s[i]-1,s[ls]);
        if(ls<=n)f[i]=(f[ls]*f[i])%p;
        if(rs<=n)f[i]=(f[rs]*f[i])%p;
    }
    printf("%lld",f[1]);
    return 0;
}

poj 1150

http://www.cppblog.com/abilitytao/archive/2009/10/31/99907.html

2*5=10

问题转换成$P(n,m)$里有多少个2，多少个5

参考这篇博文：