最小生成树
最小生成树
Kruskal:
适用稀疏图,\(O(mlogm+ma(n))\) \(a(n)\)是一次并查集的复杂度,更快,更常用
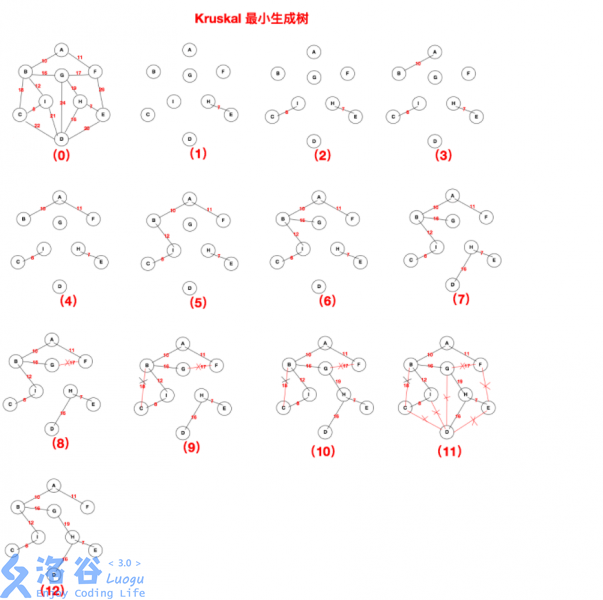
把边按照权值进行排序,用贪心的思想优先选取权值较小的边,并依次连接,若出现环则跳过此边(并查集来判断是否存在环)继续搜,直到已经使用的边的数量比总点数少一即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define M 200005
#define N 5005
#define re register
using namespace std;
inline void read(int &x){
x=0;int f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0',ch=getchar();}x*=f;
}
int n,m,fa[N],cnt,tot,ans=0,hd[M<<1],dis[N];
bool vis[N];
struct edge{
int w,v,u;
bool operator<(const edge &x){
return w<x.w;
}
}e[M*2];
inline int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
inline void kruskal(){
sort(e+1,e+m+1);
for(re int i=1;i<=m;i++){
int fu=find(e[i].u),fv=find(e[i].v);
if(fu==fv) continue;
ans+=e[i].w;
fa[fu]=fv;
if(++cnt==n-1) break;
}
}
int main(){
read(n),read(m);
int a,b,c;
for(re int i=1;i<=m;i++){
read(e[i].u),read(e[i].v),read(e[i].w);
}
for(re int i=1;i<=n;i++)
fa[i]=i;
kruskal();
printf("%d",ans);
return 0;
}
走廊泼水节
给定一棵N个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。
Solution
扫描到边\((x,y,z)\) , \(x\)所在集合为 \(S_x\) ,\(y\) 所在集合为\(S_y\) ,\(\forall u∈S_x~ ~v∈S_y\) ,要保证\(z\)是最小生成树上的边则必须使\(w(u,v)=z+1\), $ S_x\(和\) S_y$之间最多会连 \(\left|S_x\right|*\left|S_y\right|-1\) 条边
然后合并两个集合
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=60005;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int T,n,ans;
struct edge{
int u,v,w;
bool operator < (const edge &x) const {
return w<x.w;
}
}e[N<<1];
int fa[N],siz[N];
inline int find(int x) {return x==fa[x]?x:fa[x]=find(fa[x]);}
int main() {
T=read();
while(T--) {
ans=0;
n=read();
for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1;
for(int i=1;i<n;i++)
e[i].u=read(),e[i].v=read(),e[i].w=read();
sort(e+1,e+n);
for(int i=1;i<n;i++) {
int x=find(e[i].u),y=find(e[i].v);
if(x!=y) {
fa[x]=y;
ans+=(siz[x]*siz[y]-1)*(e[i].w+1);
siz[y]+=siz[x];
}
}
printf("%d\n",ans);
}
return 0;
}
Picnic Planning 度限制最小生成树
poj 1639
--> 求一个无向图的最小生成树,其中有一个点的度有限制(假设为 k)
首先我们不妨不去考虑这个有特殊限制的1号节点,那么我们去掉这个\(1\)号节点后.原图变成了 \(t\)个连通块.
那么我们对于每一个连通块,都可以在这个连通块内部求出它的最小生成树(忽略有\(1\)的边然后kruskal)
我们接下来再来考虑,如何让这些连通块与我们的一号节点相连,构成我们题目的最小生成树.
首先我们很容易求出一个相对较小的生成树.切记不是最小生成树
对于每一个连通块而言,显然要在每一个连通块之中选出一个节点(minid[ ] )与我们的1号节点的边的权值( minedge [ ] ) 最小。那么此时,我们发现我们成功将节点们连接在一起了,构成了一个较小生成树
(这里较小生成树的边已经多了,不是树了,但后面会减回来)
for(int i=2;i<=cnt;i++)
if(g[1][i]!=inf){//树上的点
int col=find(i);
if(minedge[col]>g[1][i]){
minedge[col]=g[1][i];
minid[col]=i;
}
}
for(int i=1;i<=cnt;i++)
if(minedge[i]!=inf){
t++;
tree[1][minid[i]]=tree[minid[i]][1]=1;
ans+=g[1][minid[i]];
}
那么现在的问题就是,如何优化我们的生成树,将其变成我们的最小生成树.
我们现在知道和一号节点连接的点,一共有 t 个,但是题目中要求不多于S个节点就好了.
分类讨论一下:若S<T 必然就是无解情况.
若S=T 那么此时我们的较小生成树,就是最小生成树.
若S>T 我们发现,对于一个节点而言,它不一定要属于自己原本的连通块,它可以和节点1相连
我们可以考虑无向图从节点1出发的每条边(1,x,z)其中边权z,那么假如说(1,x)这条边,它不在当前的生成树内.那么我们就可以找到从当前生成树总(1,x)这条路径上的权值最大边(u,v,w)将它删除.
如果说我添加(1,x,z)这条边,我就可以删除(u,v,w)这条边.
然后我们这颗生成树的权值就可以减少w−z
综上所述,我们每一次从每一个连通块里面找,找到让w−z的值最大的点,然后添加(1,x,z)删除(u,v,w)
直到T==S或者w−z≤0 也就是不可以加边,或者加边已经没有意义了.
#include<map>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
using namespace std;
#define N 25
#define inf 0x3f3f3f3f
#define re register
using namespace std;
int n,m,s,t,cnt,ans;
int g[N][N];
int fa[N];
bool vis[N];
map<string,int>mp;
string s1,s2;
struct Edge{
int u,v,w;
Edge() {}
Edge(int a,int b,int c) : u(a),v(b),w(c){}
bool operator < (const Edge &x)const{
return w<x.w;}
}dp[N];
vector<Edge>b;//边
bool tree[N][N];//在不在生成树内
int minid[N],minedge[N];//每个联通块到1的最小边
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
void kruskal(){
sort(b.begin(),b.end());
for(int i=0,siz=b.size();i<siz;i++){
int x=b[i].u,y=b[i].v;
if(x==1 || y==1)continue;
if(find(x)!=find(y)){
fa[find(x)]=find(y);
tree[x][y]=tree[y][x]=1;
ans+=b[i].w;
}
}
}
void dfs(int cur,int pre){
for(int i=2;i<=cnt;i++){
if(i==pre || !tree[cur][i])continue;
if(dp[i].w==-1){
if(dp[cur].w>g[cur][i])dp[i]=dp[cur];
else{
dp[i].u=cur;
dp[i].v=i;
dp[i].w=g[cur][i];
}
}
dfs(i,cur);
}
}
int main(){
memset(g,0x3f,sizeof(g));
memset(tree,0,sizeof(tree));
memset(minedge,0x3f,sizeof(minedge));
mp["Park"]=cnt=1;
for(re int i=0;i<=N;i++)fa[i]=i;
scanf("%d",&n);
for(re int i=1,x;i<=n;i++){
cin>>s1>>s2;scanf("%d",&x);
if(!mp[s1])mp[s1]=++cnt;
if(!mp[s2])mp[s2]=++cnt;
g[mp[s1]][mp[s2]]=g[mp[s2]][mp[s1]]=min(g[mp[s1]][mp[s2]],x);
b.push_back(Edge(mp[s1],mp[s2],x));
}
scanf("%d",&s);
kruskal();
for(int i=2;i<=cnt;i++)
if(g[1][i]!=inf){//树上的点
int col=find(i);
if(minedge[col]>g[1][i]){
minedge[col]=g[1][i];
minid[col]=i;
}
}
for(int i=1;i<=cnt;i++)
if(minedge[i]!=inf){
t++;
tree[1][minid[i]]=tree[minid[i]][1]=1;
ans+=g[1][minid[i]];
}
//s-t次把树变小
for(int i=t+1;i<=s;i++){
memset(dp,-1,sizeof(dp));
dp[1].w=-inf;
for(int j=2;j<=cnt;j++)
if(tree[j][1]) dp[j].w=-inf;
dfs(1,-1);
int idx,sum=inf;
for(int j=2;j<=cnt;j++)
if(sum>g[1][j]-dp[j].w){
sum=g[1][j]-dp[j].w;
idx=j;
}
if(sum>=0)break;
ans+=sum;
tree[1][idx]=tree[idx][1]=1;
tree[dp[idx].u][dp[idx].v]=tree[dp[idx].v][dp[idx].u]=0;
}
printf("Total miles driven: %d\n", ans);
return 0;
}
简单的一道
每个点向周围的点建边,然后kruskal+维护并查集大小-———注意数组要开够大
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int fa[505*505],n,x,tot,cnt,mx,siz[505*505],mp[505][505];
struct node{
int u,v,w;
node(){}
node(int a,int b,int c):u(a),v(b),w(c){}
}e[505*505*4];
bool cmp(node x,node y){
return x.w<y.w;
}
inline int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
inline int ex(int i,int j){
return (i-1)*n+j;
}
void kruskal(){
sort(e+1,e+1+cnt,cmp);
for(int i=1;i<cnt;i++){
int fu=find(e[i].u),fv=find(e[i].v);
if(fu==fv)continue;
fa[fu]=fv;
siz[fv]+=siz[fu];
if(siz[fv]>=(n*n+1)/2){
printf("%d",e[i].w);
break;
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n*n;i++)fa[i]=i,siz[i]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&mp[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(i>1) e[++cnt]=node(ex(i,j),ex(i-1,j),abs(mp[i-1][j]-mp[i][j]));//shang
if(j>1) e[++cnt]=node(ex(i,j),ex(i,j-1),abs(mp[i][j-1]-mp[i][j]));//zuo
if(i<n) e[++cnt]=node(ex(i,j),ex(i+1,j),abs(mp[i+1][j]-mp[i][j]));//xia
if(j<n) e[++cnt]=node(ex(i,j),ex(i,j+1),abs(mp[i][j+1]-mp[i][j]));//you
}
kruskal();
return 0;
}
prim
适用稠密图,复杂度 \(O(mlogn)\)(堆优化)
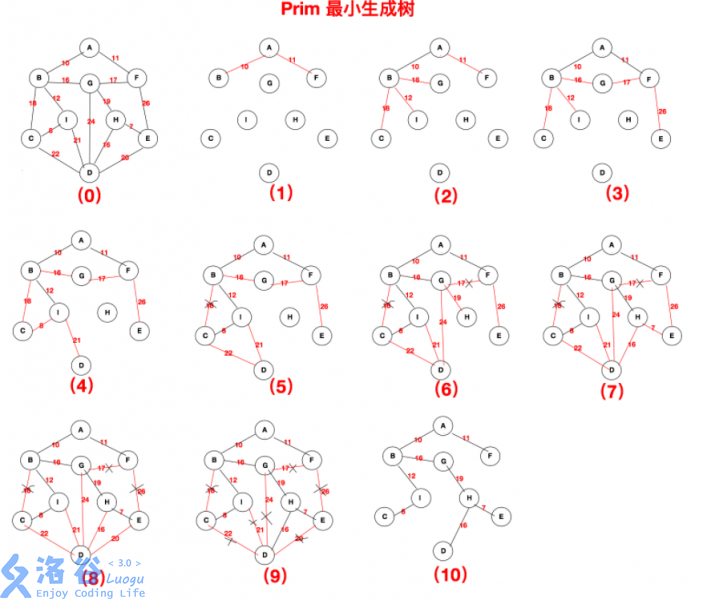
和最短路中的 dijkstra 很像,本质贪心。Prim的思想是将任意节点作为根,再找出与之相邻的所有边中边权最小的点(priority_queue),再将新节点为根更新与其相连的边的\(dis\)值(两边之和大于第三边),维护一个数组:\(dis\),作用为已用点到未用点的最短距离。
证明:Prim算法之所以是正确的,主要基于一个判断:对于任意一个顶点\(v\),连接到该顶点的所有边中的一条最短边\((v, vj)\)必然属于最小生成树(即任意一个属于最小生成树的连通子图,从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树)
#include <queue>
#include <cstdio>
#include <cstring>
#include <vector>
#include <iostream>
using namespace std;
typedef long long ll;
const int N=50005;
const int M=400005;
inline int read() {
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m;
int hd[N],to[M],nxt[M],tot,w[M];
inline void add(int x,int y,int z) {
to[++tot]=y;w[tot]=z;nxt[tot]=hd[x];hd[x]=tot;
}
#define pii pair<int,int>
#define MP make_pair
priority_queue< pii,vector<pii>,greater<pii> >q;
int ans;
int dis[N];
bool vis[N];
int cnt=0;
void prim() {
dis[1]=0;
q.push(MP(0,1));
while(q.size()&&cnt<n) {
int ww=q.top().first,x=q.top().second;
q.pop();
if(vis[x]) continue;
vis[x]=1;
ans+=ww;
cnt++;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(w[i]<dis[y])
dis[y]=w[i],q.push(MP(dis[y],y));
}
}
}
int main() {
memset(dis,0x3f,sizeof(dis));
n=read();m=read();
for(int i=1;i<=m;i++) {
int u=read(),v=read(),w=read();
add(u,v,w);add(v,u,w);
}
prim();
if(cnt==n) printf("%d\n",ans);
else puts("orz");
return 0;
}
最大生成树
①将图中所有边的边权变为相反数,再跑一遍最小生成树算法。相反数最小,原数就最大。
② 对于kruskal,将“从小到大排序”改为“从大到小排序”;
对于prim,将“每次选到所有蓝点代价最小的白点”改为“每次选到所有蓝点代价最大的点”。
poj-2728Desert King(最优比率生成树)
0/1规划来做,注意求最小生成树的时候,用prim,因为边会有n^2条
见这里
https://www.cnblogs.com/ke-xin/p/13544425.html
最短路径生成树
这不是求边权最小,而是求每个点到1号点的路径最小。
dijkstra 求出每个点到1号点的单源最短路,dis[x]=dis[fa[x]]+edge(x,fa[x]);
所有节点按dis值升序排序,仿照prim的过程,把每个节点加入,统计边权=edge(x,fa[x])的点的个数
把每一步的乘起来
#include <queue>
#include <vector>
#include <cstdio>
#include <utility>
#include <cstring>
#include <iostream>
using namespace std;
const int N=1005;
const int M=2000005;
const int mod=2147483647;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m;
int hd[M],nxt[M],to[M],tot,w[M];
inline void add(int x,int y,int z) {
to[++tot]=y;w[tot]=z;nxt[tot]=hd[x];hd[x]=tot;
}
priority_queue< pair<int,int> >q;
bool vis[N];
int dis[N];
void dij() {
memset(dis,0x3f,sizeof(dis));
q.push(make_pair(0,1));
dis[1]=0;
while(!q.empty()) {
int x=q.top().second,d=q.top().first;q.pop();
if(vis[x]) continue;
vis[x]=1;
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(dis[y]>dis[x]+w[i]) {
dis[y]=dis[x]+w[i];
if(!vis[y]) q.push(make_pair(-dis[y],y));
}
}
}
}
int cnt[N];
int main() {
n=read();m=read();
for(int i=1,x,y,z;i<=m;i++) {
x=read();y=read();z=read();
add(x,y,z);
add(y,x,z);
}
dij();
for(int x=1;x<=n;x++)
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(dis[y]==dis[x]+w[i]) cnt[y]++;
}
long long ans=1;
for(int i=1;i<=n;i++)
if(cnt[i]) ans=ans*cnt[i]%mod;
printf("%lld\n",ans%mod);
return 0;
}

