7.13
7.13模拟赛
T1 sign
签到题。。。
只会暴力dfs...本能骗到70分
出题人血坑。。。
先读入边权
最后惨遭爆零
先附上70代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int N=10005;
int n,m=0,in[N],w[N],st[N];
vector< pair<int,int> >g[N<<1];
long long ans;
void dfs(int x,int fa) {
int siz=g[x].size();
for(int i=0;i<siz;i++) {
int y=g[x][i].first;
if(y==fa)continue;
w[y]+=w[x]+g[x][i].second;
ans+=w[y];
dfs(y,x);
}
}
int main() {
freopen("sign.in","r",stdin);
freopen("sign.out","w",stdout);
n=read();
for(int i=1,x,y,z;i<n;i++) {
x=read();y=read();z=read();
g[x].push_back(make_pair(y,z));
g[y].push_back(make_pair(x,z));
in[x]++;in[y]++;
}
for(int i=1;i<=n;i++)
if(in[i]==1)
st[++m]=i;
int cnt=0;
for(int i=1;i<=m;i++) {
dfs(st[i],0);
memset(w,0,sizeof(w));
}
printf("%lld\n",ans);
return 0;
}
正解——
按边考虑,记录其子树的叶子结点sonleaf [ ] ,然后记录子树大小siz[ ] ,dfs遍历一遍统计所有siz和sonleaf
ans=(外面的点son_leaf+里面的点(cnt_sonleaf - sonleaf ) )*边权
#include <iostream>
#include <cstdio>
using namespace std;
const int MAXN=500005;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,hd[MAXN];
struct node {
int from,to,w,nxt;
}e[MAXN];
int tot;
void add(int fr,int to,int val) {
e[++tot].from=fr;
e[tot].to=to;
e[tot].w=val;
e[tot].nxt=hd[fr];
hd[fr]=tot;
}
int root;
int du[MAXN];
bool ch[MAXN];
int cnt_leaf;
int siz[MAXN],son_leaf[MAXN];
int to_fa[MAXN];
void dfs(int x,int fa){
siz[x]++;
for(int i=hd[x];i;i=e[i].nxt) {
if(e[i].to==fa) {
to_fa[x]=i;
continue;
}
dfs(e[i].to,x);
siz[x]+=siz[e[i].to];
son_leaf[x]+=son_leaf[e[i].to];
}
}
long long ans;
int main() {
n=read();
for(int i=1,u,v,w;i<=n-1;i++) {
w=read();u=read();v=read();
add(u,v,w),add(v,u,w);
du[u]++,du[v]++;
}
for(int i=1;i<=n;i++) {
if(du[i]==1) {
cnt_leaf++;son_leaf[i]=1;
}
else root=i;
}
dfs(root,0);
for(int i=1;i<=n;i++) {
if(i==root) continue;
long long cnt=0;
cnt+=(son_leaf[i]*(n-siz[i]));
cnt+=((cnt_leaf-son_leaf[i])*siz[i]);
ans+=cnt*e[to_fa[i]].w;
}
printf("%lld\n",ans);
return 0;
}
T2map
Description
一张n个点的无向完全图,从1号点出发,每秒随机沿当前点的出度移动一条边。q次询问,每次给出一个数t[i],询问第t[i]秒在1号点的概率,答案对998244353取模。
法一:大力推式子——找规律
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;
inline LL read() {
LL x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const LL p = 998244353;
LL n,m,t;
LL pow(LL a,LL b) {
LL ans=1;a=(a+p)%p;
while(b) {
if(b&1) ans=(ans*a)%p;
a=(a*a)%p;
b>>=1;
}
return ans%p;
}
LL inv(LL x) {
return pow(x,p-2);
}
int main() {
n=read()-1;m=read();
while(m--) {
t=read();
if(t==0) {
puts("1");continue;
} else if(t==1) {
puts("0");continue;
} else {
LL c=inv((pow(n,t)+pow(n,t-1))%p);
if(t&1) {
printf("%lld\n",(pow(n,t-1)-1+p)%p*c%p);
} else {
printf("%lld\n",(pow(n,t-1)+1)%p*c%p);
}
}
}
return 0;
}
法二:构造矩阵,矩阵快速幂
#include <cstdio>
#include <iostream>
#include <cstring>
typedef long long ll;
inline ll read() {
ll x=0;int f=1;char ch=getchar();
while(!isdigit(ch)){ch=='-'&&(f=-1);ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
using namespace std;
const int P = 998244353;
inline void ADD(ll &a, ll b) {
a += b;
if (a >= P) a -= P;
}
struct matrix{
int n, m;
ll h[5][5];
matrix() {
n = m = 0;
memset(h, 0, sizeof(h));
}
matrix operator *(const matrix a) const {
matrix mt;
mt.n = n, mt.m = m;
for (register int k = 1; k <= m; ++k) {
for (register int i = 1; i <= n; ++i) {
for (register int j = 1; j <= m; ++j) {
ADD(mt.h[i][j], h[i][k] * a.h[k][j] % P);
}
}
}
return mt;
}
};
inline ll quickpow(ll x, ll k) {
x %= P;
ll res = 1;
while (k) {
if (k & 1) res = res * x % P;
x = x * x % P;
k >>= 1;
}
return res;
}
inline matrix Qp(matrix x, ll k) {
matrix res = x; --k;
while (k) {
if (k & 1) res = res * x;
x = x * x;
k >>= 1;
}
return res;
}
ll n, q;
int main() {
n=read();q=read();
matrix A, B;
A.n = 1, A.m = B.n = B.m = 2;
A.h[1][1] = 1;
B.h[1][2] = 1;
B.h[2][1] = quickpow(n - 1, P - 2);
B.h[2][2] = (n - 2) % P * quickpow(n - 1, P - 2) % P;
for (register int i = 1; i <= q; ++i) {
ll t; t=read();
if (t == 0) {
puts("1");
continue;
}
matrix C = A * Qp(B, t);
printf("%lld\n", C.h[1][1]);
}
return 0;
}
T3path
好吧,我还是只会暴力。。。菜炸了55分
spfa 最短路。。。刘队说这稀疏图spfa肯定挂了,啊好像dij 能多骗5分。。。算了
说正解吧——还有俩正解
线段树优化建图
适用情况
当点数很多,并且边集以区间形式 (点-->区间/区间->点) 给出
强行连边复杂度太大,考虑如何维护同一个子区间的连边,使用线段树优化。
优化思路
先考虑 点-->区间 连边的部分。
考虑建图的复杂度真正体现在哪里。
如果所有的被连边区间不交,那么总复杂度是对的。
所以真正建图的复杂度,产生在被连边区间相交的部分,尤其是一个同一个区间被多个点连边,那么我们每一个都要产生区间长度的代价。
那么有一个思路,如果有一个区间被多次连边,那么不妨我们建立这个区间的一个代表节点。
首先预处理的时候将这个代表节点(虚点)连向区间里的每一个节点,边权为 0,就代表了 连向代表节点的每一条边 都连向了区间里的每一个节点,然后都每次都将边连向这个代表节点即可。
建图过程 (点 -->区间)
但是注意到这种区间并不是很好找,这种找区间的方法并不是具有很强的普适性。
我们知道线段树的每一个节点维护的是一个固定的区间,线段树的区间操作是 log 的。
回忆区间加的过程,如果一个节点的代表区间被完全覆盖,那么我们会在这个节点上打标记,等到需要的时候再下传。这体现了一种代表的关系,即区间共有的性质我可以只标记在代表这个区间的节点上。
如果要从一个点连向一个区间,那么可以像区间加那样,把这个点向完全覆盖的区间连边。
也就是说,在区间连边时,在线段树上每找到一个完全覆盖的节点,就将出发点向这个区间的代表节点连边。
同样的,我们先考虑预处理。
一个节点被连边,代表这个节点的 子树 都可以到达。
之所以强调子树,而不是强调区间里的每一个节点,因为我们预处理的边只会向下 连一层 。
只连下一层的边数量级是 O(2N) ,而连向区间里的每一个节点显然每一层都是O(N) ,总的边的数量级就是 $O(Nlog_2N) $,边的级别显然大了很多,并且也不符合线段树的关系定义。
一个8个节点的线段树预处理之后的连边情况如图所示。图中边权全部为 0。
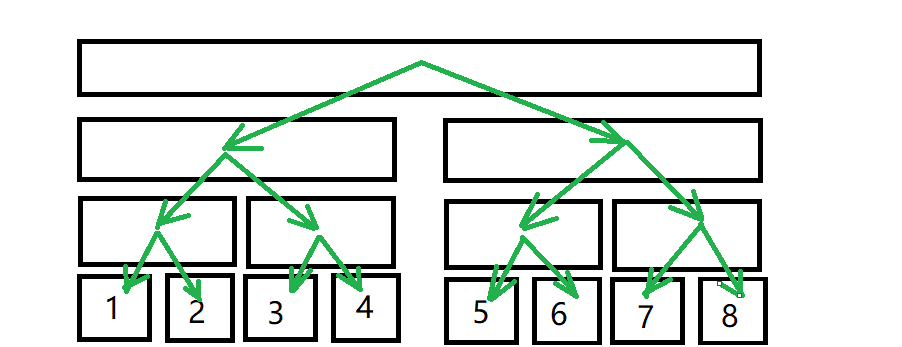
然后一条连边就可以按照我们说的那样了,找到对应的区间就好。
假如8 号点要向区间 [2,5] 连边,最后会是蓝边的样子(边权就省略了):
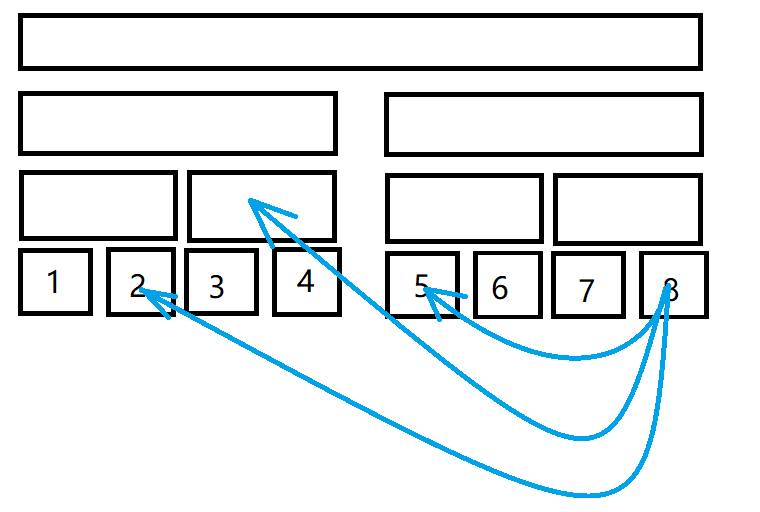
建图过程 (区间 -->点)
发现原来线段树的区间传递关系并不对了。
如果我们找到了每一段区间,直接向指向的点连边,子树内真正建边的点并没有连出这一条边。
如图,如果要区间[5,8]向T 连边,蓝框框起来的点并没有真正向T 连边。
因为建树的时候绿色边的方向是向区间内传递的。
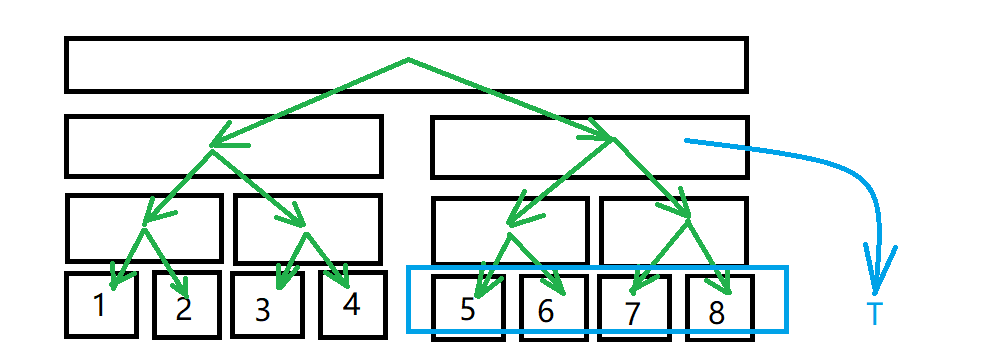
很容易想到反向再建一棵树。显然叶节点是相同的,所以两棵树会共用叶节点。
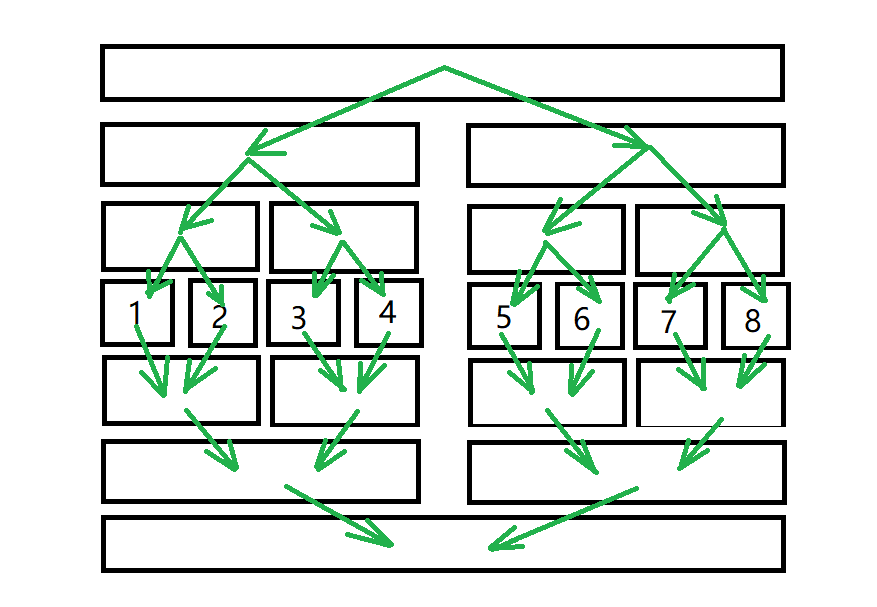
倒着的树上传递关系就变为,一个节点连了出边,那么他所代表的区间里所有节点都向外连了一条出边。
同理,这些绿色的边的边权都是0 。
关于正确性,显然更大的区间并不会到达小区间,所以连边不用担心范围超界。
此时我们就可以在倒着的树上找所有的区间,然后连出边就可以了。
总结:
1.建立两个线段树,一个是入树,一个是出树(动态开点)
2.连边:
建立两个虚点,虚点之间边权不为0
从入树找到出发区间对应的节点,从这些节点向其中一个虚点连接边权为0的边,从出树找到到达区间对应的节点,从另一个虚点向对应的节点连接边权为0的边

Solution
我们对每一条信息都单独开出来一个转移节点,然后就变成了 区间--> 点和 点-->区间的问题了。
但是双向边不能共用一个转移节点。因为这样其实上在 $ [l_1,r_1] $内的每个点之间都连了一条长度为2 的边。
实际做的时候,对每一个单向边都开一个转移节点,然后出边边权都设为 0,入边边权都设为 1就可以了。
还有一个比较妙的方法,是出入边权都设为1 然后最短路的答案除以2 ,也是可以的。
最短路不用 dij ,双端bfs即可 (0扔前面,1扔后面)
my代码:
#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int N=12000010;
int n,m,s,rt_in,rt_out,tot;
int ls[N],rs[N];
int in[N],out[N];
int hd[N],e_cnt;
struct node{
int id,val;
node(){}
node(int a,int b):id(a),val(b){}
};
struct edge{
int to,nxt,w;
edge(){}
edge(int a,int b,int c):to(a),nxt(b),w(c){}
}e[N];
inline void add(int x,int y,int z){
e[++e_cnt]={y,hd[x],z};hd[x]=e_cnt;
}
inline void build_in(int l,int r,int &p){
p=++tot;
if(l==r){in[l]=p;return;}
int mid=(l+r)>>1;
build_in(l,mid,ls[p]);
build_in(mid+1,r,rs[p]);
add(ls[p],p,0);
add(rs[p],p,0);
}
inline void build_out(int l,int r,int &p){
p=++tot;
if(l==r){out[l]=p;return;}
int mid=(l+r)>>1;
build_out(l,mid,ls[p]);
build_out(mid+1,r,rs[p]);
add(p,ls[p],0);
add(p,rs[p],0);
}
inline void insert_in(int ql,int qr,int l,int r,int cur,int p){
if(ql<=l&&r<=qr){add(p,cur,1);return;}
int mid=(l+r)>>1;
if(ql<=mid) insert_in(ql,qr,l,mid,cur,ls[p]);
if(qr>mid) insert_in(ql,qr,mid+1,r,cur,rs[p]);
}
inline void insert_out(int ql,int qr,int l,int r,int cur,int p){
if(ql<=l&&r<=qr){add(cur,p,1);return;}
int mid=(l+r)>>1;
if(ql<=mid) insert_out(ql,qr,l,mid,cur,ls[p]);
if(qr>mid) insert_out(ql,qr,mid+1,r,cur,rs[p]);
}
int dis[N];
bool vis[N];
void work(){
deque <node> q;
memset(dis,0x3f,sizeof(dis));
dis[in[s]]=0;q.push_front({in[s],0});
while(!q.empty()){
int x=q.front().id;q.pop_front();
if(vis[x])continue;
vis[x]=1;
for(int i=hd[x];i;i=e[i].nxt){
int y=e[i].to,z=e[i].w;
if(dis[y]>dis[x]+z){
dis[y]=dis[x]+z;
if(!vis[y]){
if(!z) q.push_front({y,dis[y]});
else q.push_back({y,dis[y]});
}
}
}
}
}
int main(){
n=read();m=read();s=read();
build_in(1,n,rt_in);
build_out(1,n,rt_out);
for(int i=1;i<=n;i++) add(in[i],out[i],0),add(out[i],in[i],0);
for(int i=1;i<=m;i++){
int l1=read(),r1=read(),l2=read(),r2=read();
tot++;insert_in(l1,r1,1,n,tot,rt_in),insert_out(l2,r2,1,n,tot,rt_out);
tot++;insert_in(l2,r2,1,n,tot,rt_in),insert_out(l1,r1,1,n,tot,rt_out);
}
work();
for(int i=1;i<=n;i++)
printf("%d\n",dis[out[i]]/2);
return 0;
}
hs_black更优秀做法https://www.luogu.com.cn/blog/hs-black/solution-p6348
老师
std:
#include<bits/stdc++.h>
#define N 1000010
#define M 4000010
#define Rg register
#define mid ((l + r) >> 1)
using namespace std;
inline int rd() {
int x = 0;
bool f = 0;
char c = getchar();
while (!isdigit(c)) {
if (c == '-') f = 1;
c = getchar();
}
while (isdigit(c)) {
x = x * 10 + (c ^ 48);
c = getchar();
}
return f ? -x : x;
}
int n, m, s, cnt, tot, hd[N << 3];
struct edge{
int w, to, nxt;
} e[M << 1];
inline void add(int u, int v, int w) {
e[++tot].to = v;
e[tot].w = w;
e[tot].nxt = hd[u];
hd[u] = tot;
}
struct segmentin{
int root, ptr;
inline int newnode(){return ++ptr;}
struct node{int ls, rs, p;}c[N << 1];
void build(int &rt, int l, int r) {
rt = newnode();
if(l == r) {
c[rt].p = l;
return;
}
build(c[rt].ls, l, mid);
build(c[rt].rs, mid + 1, r);
c[rt].p = ++cnt;
add(c[rt].p, c[c[rt].ls].p, 0);
add(c[rt].p, c[c[rt].rs].p, 0);
}
void updata(int rt, int l, int r, int L, int R, int p, int w) {
if(l > R || r < L) return;
if(l >= L && r <= R) {
add(p, c[rt].p, w);
return;
}
if(L <= mid) updata(c[rt].ls, l, mid, L, R, p, w);
if(R > mid) updata(c[rt].rs, mid+1, r, L, R, p, w);
}
}treein;
struct segmentout{
int root, ptr;
inline int newnode(){return ++ptr;}
struct node{int ls, rs, p;}c[N << 1];
void build(int &rt, int l, int r) {
rt = newnode();
if(l == r) {
c[rt].p = l;
return;
}
build(c[rt].ls, l, mid);
build(c[rt].rs, mid + 1, r);
c[rt].p = ++cnt;
add(c[c[rt].ls].p, c[rt].p, 0);
add(c[c[rt].rs].p, c[rt].p, 0);
}
void updata(int rt, int l, int r, int L, int R, int p, int w) {
if(l > R || r < L) return;
if(l >= L && r <= R) {
add(c[rt].p, p, w);
return;
}
if(L <= mid) updata(c[rt].ls, l, mid, L, R, p, w);
if(R > mid) updata(c[rt].rs, mid + 1, r, L, R, p, w);
}
}treeout;
int dis[N << 3];
bool vis[N << 3];
priority_queue<pair<int, int> >q;
inline void dij(){
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0; q.push(make_pair(0, s));
while(!q.empty()) {
int u = q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(Rg int i = hd[u], v; i; i = e[i].nxt)
if(dis[v = e[i].to] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
q.push(make_pair(-dis[v], v));
}
}
}
int main(){
cnt = n = rd();
m = rd();
s = rd();
treein.build(treein.root, 1, n);
treeout.build(treeout.root, 1, n);
for(Rg int i = 1, l1, r1, l2, r2; i <= m; ++i) {
++cnt;
l1 = rd();
r1 = rd();
l2 = rd();
r2 = rd();
treein.updata(treein.root, 1, n, l1, r1, cnt, 1);
treeout.updata(treeout.root, 1, n, l2, r2, cnt, 1);
++cnt;
treein.updata(treein.root, 1, n, l2, r2, cnt, 1);
treeout.updata(treeout.root, 1, n, l1, r1, cnt, 1);
}
dij();
for(Rg int i = 1; i <= n; ++i)
printf("%d\n", dis[i] / 2);
return 0;
}

