异或哈希

1|0理论基础

异或哈希是个很神奇的算法，利用了异或操作的特殊性和哈希降低冲突的原理，可以用于快速找到一个组合是否出现、序列中的数是否出现了k次

https://blog.csdn.net/notonlysuccess/article/details/130959107

2|0CF1175F

https://codeforces.com/contest/1175/problem/F

那么，最经典的求组合出现问题

理论基础中提到了这个问题，并给出了 $O (n^{2})$ 的暴力解法。

std::mt19937_64 rnd(time(0));
using hash = uint64_t;

void solve()
{
    int n; std::cin >> n;
    std::vector<int> a(n); for (auto& x : a) {std::cin >> x;}
    std::vector<hash> code(n + 1), pre_chk(n + 1), pre_xor(n + 1);
    // code:(a[i] -> uint64)， pre_chk : 1 ~ n 的 前缀异或和， pre_xor : a[i] 的 前缀异或和
    for (int i = 1; i <= n; i++) {
        code[i] = rnd();
        pre_chk[i] = pre_chk[i - 1] ^ code[i];
    }
    for (int i = 1; i <= n; i++) {pre_xor[i] = pre_xor[i - 1] ^ code[a[i]];}

    std::map<int, int> cnt; cnt[0] = 1;

    int res{}; for (int l = 1; l <= n; l++) {
        for (int r = l; r <= n; r++) {
            if (pre_xor[r] ^ pre_xor[l - 1] == pre_chk[r - l + 1]) {
                res += 1;
            }
        }
    }
}

根据问题进一步提取性质：

满足条件的区间肯定有 $1$ 和 等于区间长度的最大值 $m x$
分类 $m x$ 在 $1$ 的左边或者右边处理即可。

int ans{}, one{};//特殊记录长度为1的个数，因为会统计两边

auto calc = [&](auto a) {//正反跑一遍，处理两个方向的方案数
    std::vector<hash> pre_xor(n + 1);//a[i] 的 前缀异或和和
    for (int i = 0; i < n; i++) {pre_xor[i + 1] = pre_xor[i] ^ code[a[i]];}
    int lst_one{-1}, mx = 0; for (int r = 0; r < n; r++) {
        if (a[r] == 1) {//进行新一段的处理
            one += 1; lst_one = r; mx = 1;    
        } else if (lst_one != -1) {
            mx = std::max(mx, a[r]);
            if (mx >= (r - lst_one + 1)) {//如果当前最大值大于等于当前段长度，则可以操作
                int l{lst_one - (mx - (r - lst_one + 1))};//找到符合当前最大值长度的段的左端点
                if (l >= 0) {ans += ((pre_xor[r + 1] ^ pre_xor[l]) == pre_chk[mx]);}
            }
        }
    }

};
calc(decltype(a)(a.begin(), a.end())); calc(decltype(a)(a.rbegin(), a.rend()));

std::cout << ans + one / 2 << '\n';

3|0CF1418G

https://www.luogu.com.cn/problem/CF1418G

那么，出现次数问题

这里要求出现三次，所以不用二进制异或而是新定义一个三进制异或：

0 \oplus 0 = 0 0 \oplus 1 = 1 0 \oplus 2 = 2 1 \oplus 2 = 0

constexpr int N{60};
using ternary = std::array<int, N>;

ternary operator ^(const ternary &a, const ternary &b){
    ternary c;
    for (int i = 0; i < N; i++) {
        c[i] = a[i] + b[i];
        if (c[i] >= 3) c[i] -= 3;
    }
    return c;
}

首先我们知道一个思想，证明充要条件就要证明它既充分又必要；同样，要证明一个数等于某个值，必须让它既小于等于又大于等于这个值。
这个思想运用到这道题上就十分方便。我们让所有数的出现个数 $c n t = 3$ ，便是要去满足 $c n t \geq 3 \land c n t \leq 3$ 这俩约束。 |

第一个约束十分好想，可以规约到 $c n t \equiv 0 (\mod 3)$ 上去（三的倍数必然大于等于三），然后显然用 XOR-Hash 搞一下就行。

然后考虑第二个约束。我们考虑使用类似于双指针的算法，具体来说：考虑对于一个满足约束二的 $[l, r]$ 区间，右指针每次往右移动一次，都可能会破坏原本“满足约束二”的性质。那么为了让其重新满足，我们需要让左指针一直向右移动，即：从左到右删去数字使得区间再次满足约束二。(只需让新加入的右指针的值 $a_{r}$ 出现的次数小于等于三即可；因为这样删除必然不会导致“因为其他数字出现次数减少而导致不能满足约束二”这种情况，理由显然）

令 $p r e_{r}$ 为 $[1, r]$ 区间的异或和（也就是到 $r$ 为止的前缀异或和）。当删除完毕之后，我们统计满足 $p r e_{r} = p r e_{p o s}$ 且 $p o s \in [l, r]$ 的 $p o s$ 数量，这一点可以使用 map 或者哈希表完成。那么这道题就完成了，复杂度 $O (N \log_{2} N)$ 或者纯线性。

void solve()
{
    int n; std::cin >> n; std::vector<int> a(n); for (auto& x : a) {std::cin >> x; --x;}
    std::vector<ternary> nums(n); for (int i = 0; i < n; i++) for (int j = 0; j < N; j++) {nums[i][j] = rnd() % 3;}

    std::vector pos(n, std::vector<int>());//(数字，出现位置)
    std::vector<ternary> pre_xor(1);//(前缀异或和)
    std::map<ternary, int> cnt;//(统计前缀异或和值的出现次数)
    cnt[pre_xor[0]] = 1;
    int p{}; i64 ans{};
    for (int i = 0; i < n; i++) {
        pre_xor.push_back(pre_xor.back() ^ nums[a[i]]);//当前目标的前缀异或和
        pos[a[i]].push_back(i);
        if (std::size(pos[a[i]]) > 3) {//如果该数字的出现次数已经大于三次了
            while (p <= pos[a[i]][std::ssize(pos[a[i]]) - 4]) {//去掉直到最左边的该数字的位置所有出现的数字, 并更新每个前缀异或和出现的次数
                cnt[pre_xor[p]] -= 1; p++;
            }
        }
        ans += cnt[pre_xor.back()];
        cnt[pre_xor.back()] += 1;
    }
    std::cout << ans << '\n';
}

4|0CF1996G

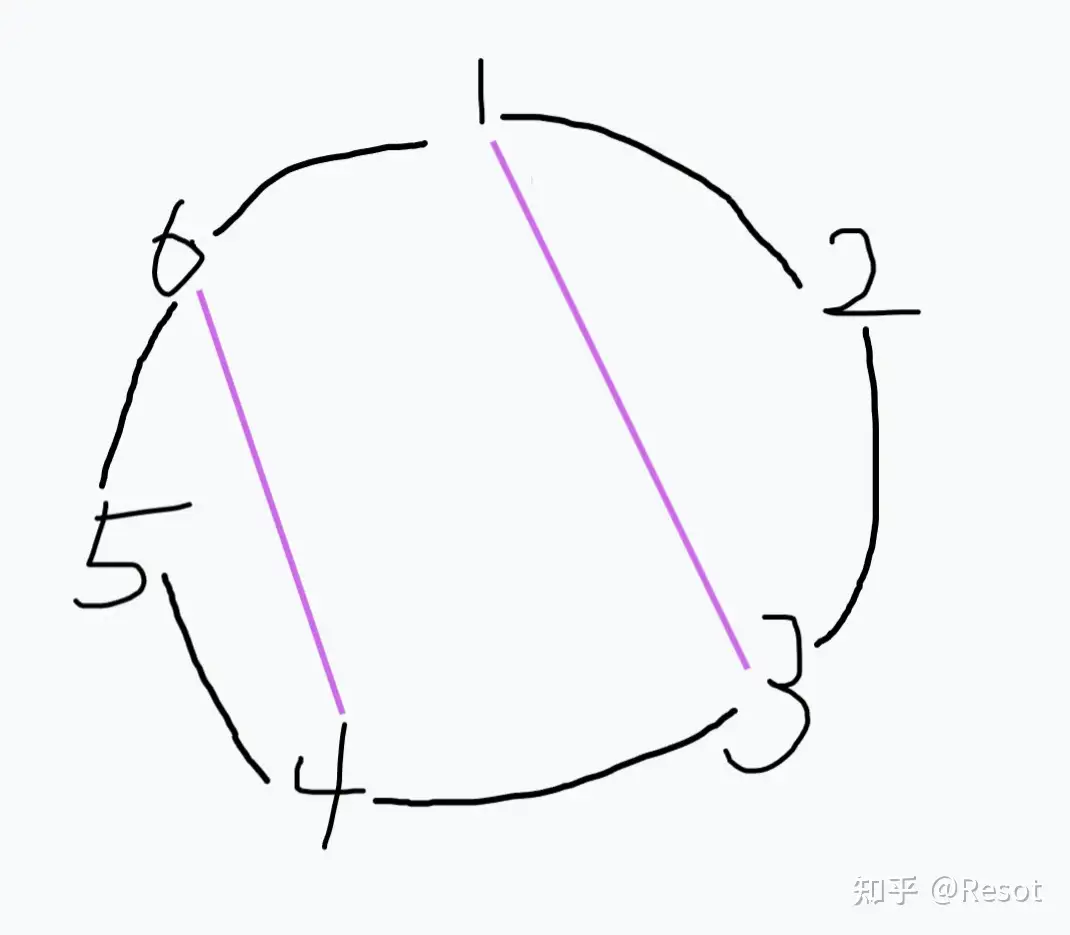
https://www.luogu.com.cn/problem/CF1996G

很神奇的哈希做法

我们设 $n = 6, m = 2$ ，且 $(1, 3), (4, 6)$ 是朋友，用紫线的链接表示朋友关系

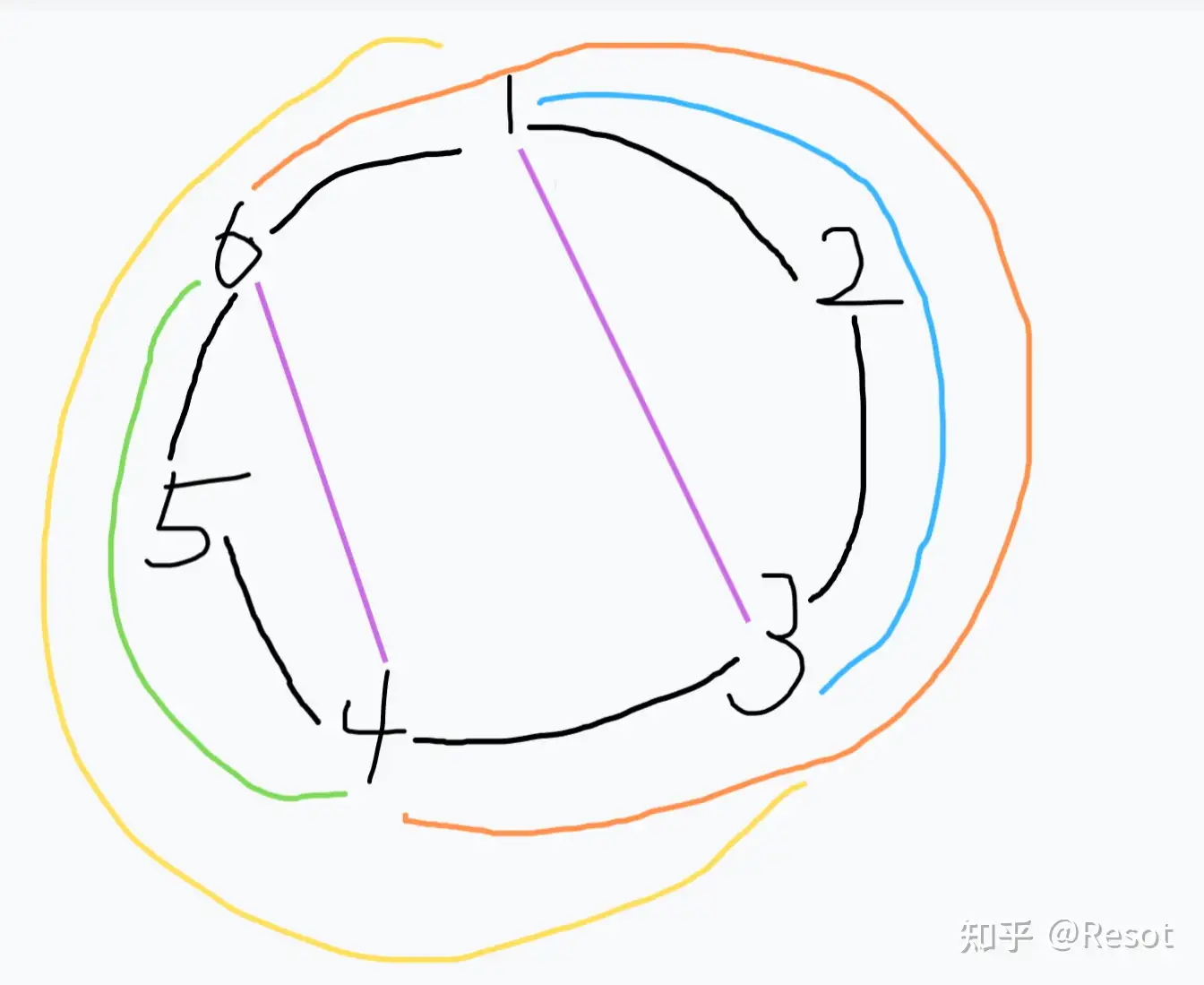
对于每对朋友，要么是通过优弧联通，要么是通过劣弧联通，所以我们干脆直接对优弧劣弧都染色一下

其中绿色/橙色是 $(4, 6)$ 的劣弧/优弧，蓝色/黄色是 $(1, 3)$ 的劣弧/优弧

要维护最少的路，就是通过我们对于每队朋友都选择他们的劣弧/优弧后使得没有被染色的道路最多（我们选择某队朋友的劣弧后，就使得优弧不存在图上了）

一个很经典的思路：保留最少相当于删除最多

为了方便写博客，我们分别对上面颜色的曲线进行编号：绿色是1，黄色是2，橙色是3，蓝色是4

那么我们能选择的弧的集合其实是 $(1, 3), (2, 3), (1, 4), (2, 4)$

其实就是我们要对每对朋友都选择一个弧，使得仅被这些弧染色的道路尽可能多，然后删除这些道路

我们改怎么实现这个想法呢？

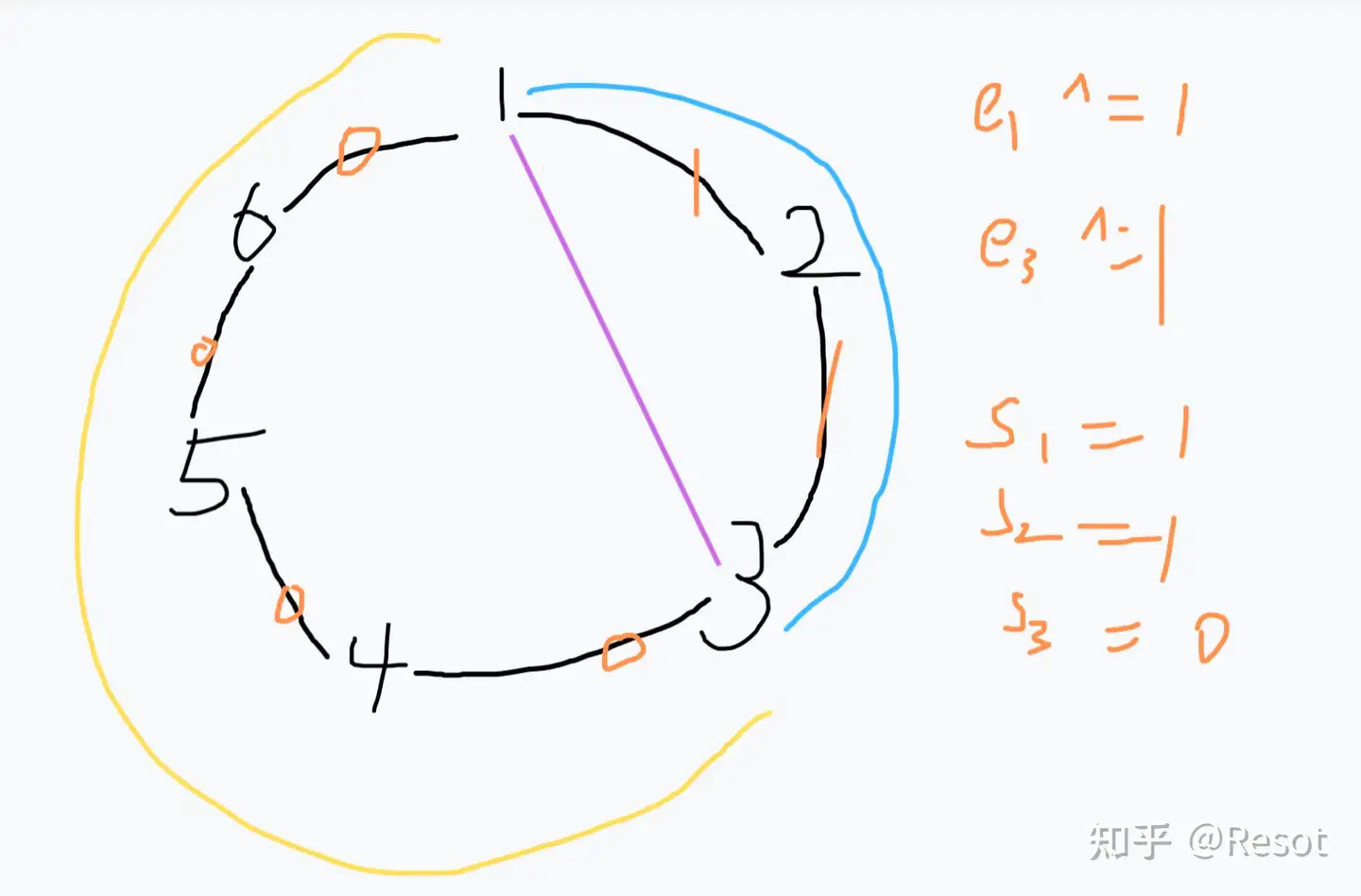
我们定义 $e d g e_{i}$ 为 $i \to i + 1$ 的这条边，例如 $e d g e_{1}$ 就是 $1$ 连向 $2$ 的道路

我们对每对朋友的两个端点都 $\oplus r a n d$ ，其中 $r a n d$ 是一个六十四位随机数，即对于 $(1, 3)$ 有 $e d g e_{1} \oplus r a n d, e d g e_{3} \oplus r a n d$ ，其中 $r a n d$ 仅在这里是相同的，即每对朋友在异或时的 $r a n d$ 都互不相同。

然后我们维护一个前缀和就可以得到 $i \to i + 1$ 这条路的染色情况了

而这是非常抽象的，我们是怎么得到染色情况的呢？并且我们不是只染了一个弧吗，另一个难道直接不管了？

首先我们先简化模型，假设只有 $(1, 3)$ 这一对朋友，并且我们恰好得到 $r a n d = 1$ ，那么有

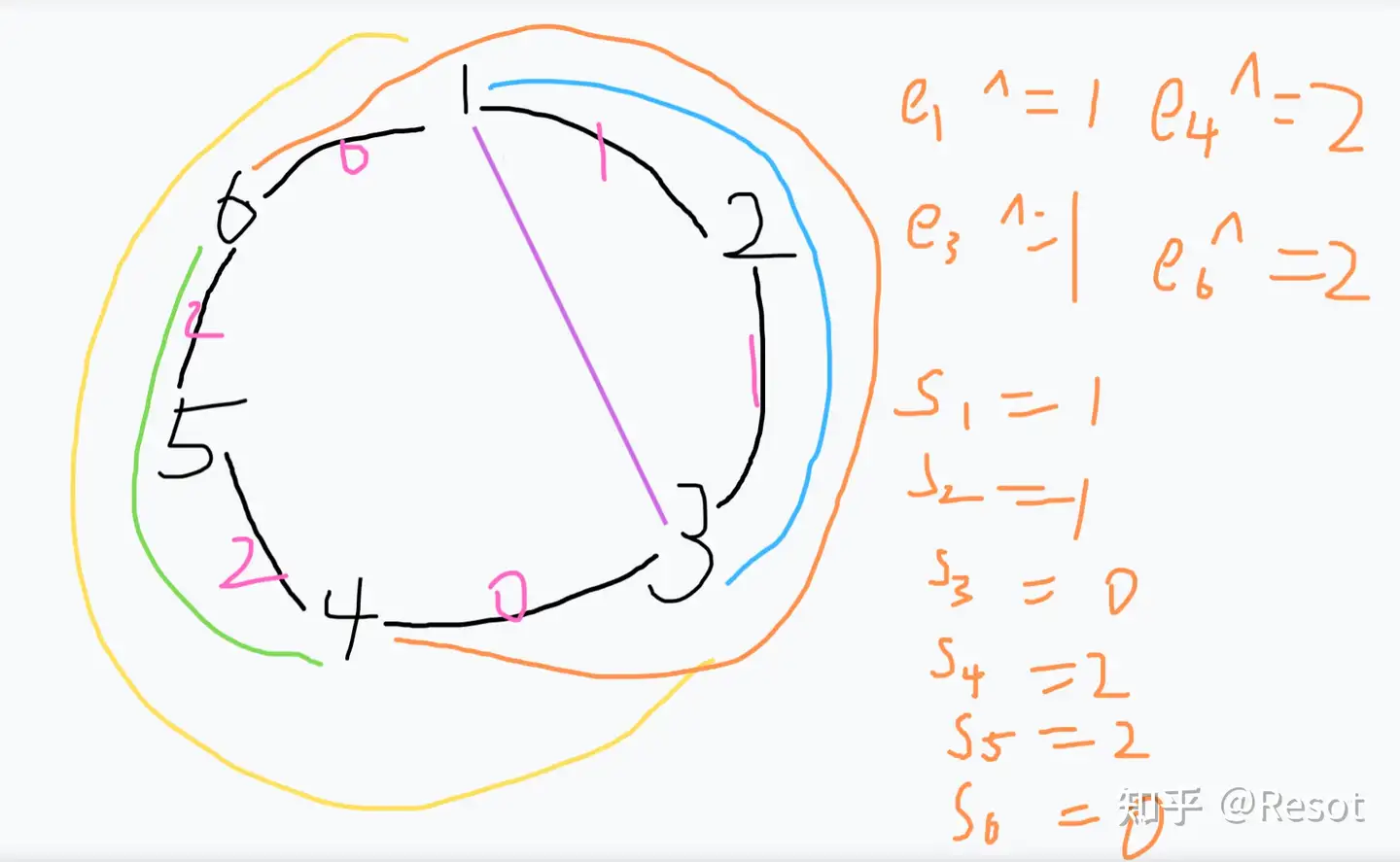
然后又加上了 $(4, 6)$ 这对朋友，并且 $r a n d$ 恰好是 $2$

可以发现神奇的每个数值刚好都对应着一种弧的集和

我们对两端都异或同一个随机数是通过差分的思想来 $O (1)$ 染色，这样可以通过前缀和得知当前的染色情况

可以通过前缀和得知染色情况是因为，我们通过六十四位的随机数异或值实现了哈希的思想，对于每种弧都有特定的哈希值，而弧集的哈希值是可以通过异或得到，这个比较抽象，所以建议可以理解为状压差不多的思想

还有一个问题：为什么只对一个弧染色就相当于对两个弧都染色了呢

因为是异或的随机值，我们对优弧染上了 $x$ ，对劣弧染上了 $y$ ,然后整个圈都同时异或 $y$ ，相当于优弧染上了 $x \oplus y$ ，劣弧染了 $0$ ，因为是随机的异或值，所以 $x \oplus y$ 可以直接相当于 $x$ 。

然后用统计下前缀和出现最多的数值，删除这个数就是答案

std::mt19937_64 rng {std::chrono::steady_clock::now().time_since_epoch().count()};

void solve()
{
#define tests
	int n, m; std::cin >> n >> m;
	std::vector<u64> f(n);
	for (int i = 0, u, v; i < m; i++) {
		std::cin >> u >> v; --u; --v; u64 rnd{rng()};
		f[u] ^= rnd; f[v] ^= rnd;//相当于差分对优弧劣弧染色
	}
	// 要维护最少的路，就是通过我们对于每队朋友都选择他们的劣弧/优弧后使得没有被染色的道路最多
	// 我们选择某队朋友的劣弧后，就使得优弧不存在图上了
	// 因为是异或的随机值，我们对优弧染上了 x ，对劣弧染上了 y ,然后整个圈都同时异或 y
	// 相当于优弧染上了 x⊕y，劣弧染了 0，因为是随机的异或值，所以 x⊕y 可以直接相当于 x。
	// 所以前缀和随便选一个分界点都能代表一种全染色情况，要么优弧，没值的久全是劣弧
	std::map<u64, int> cnt;
	u64 pre{};
	int mx{};
	for (int i = 0; i < n; i++) {
		pre ^= f[i]; cnt[pre] += 1; mx = std::max(mx, cnt[pre]);
	}
	std::cout << n - mx << '\n';
}

__EOF__

本文作者：Kdlyh
本文链接：https://www.cnblogs.com/kdlyh/p/18333737.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！