浅谈遗传算法
由于网上遗传算法的博客要么是例题不足,要么是过于工程化,所以准备写一篇更加亲民的博客。篇幅不长,深入浅出。由于笔者能力有限,可能出现部分错误。
1|0概述
就不从百度上往下搬了。
遗传算法,又称为
特别提醒,遗传算法是一个随机算法,会有一定的错误概率。
2|0前置知识
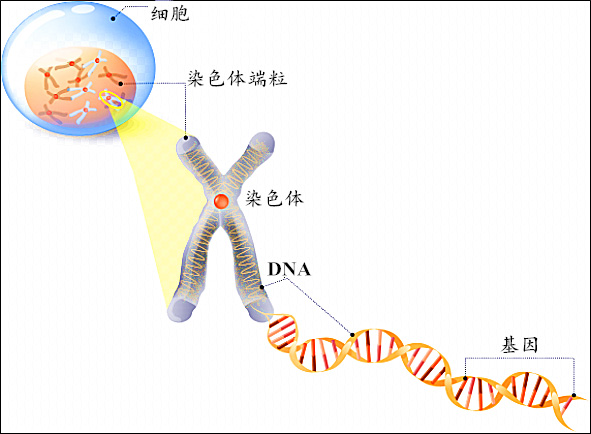
首先先来补充一些生物知识:
每个生物都有许许多多的染色体,这些染色体呈棒状。每个染色体主要由双螺旋状的
大概不需要过多解释,中学生物都学过。将 个体,染色体,基因 范围由大到小排序为 :
个体(Individual) > 染色体(chromosome) > 基因(gene)
遗传算法模拟了自然选择的过程。那些适应环境的个体能够存活下来并且繁殖后代。那些不适应环境的个体将被淘汰。换言之,如果我们对每个个体都有一个适应度评分(用来评价其是否适应环境),那么对于适应度高的物体来说,将具有更高的繁殖和生存的机会。
另外,为了保持种族的稳定性,我们会将父代的基因传递下去。
3|0基础理论
遗传算法基于一些不证自明的理论依据:
- 种群中的个体争夺资源和交配。
- 那些成功的(最适合的)个体交配以创造比其他人更多的后代。
- 来自 “最适” 父母的基因在整个世代中传播,即有时父母创造的后代比父母任何一方都好。
- 因此,每一代人都更适合他们的环境。
4|0基础概念
拿古代人类来举例子:
- 个体(
- 种群(
- 种群个体数(
- 染色体(
- 基因(
- 适应度(
- 迭代次数(
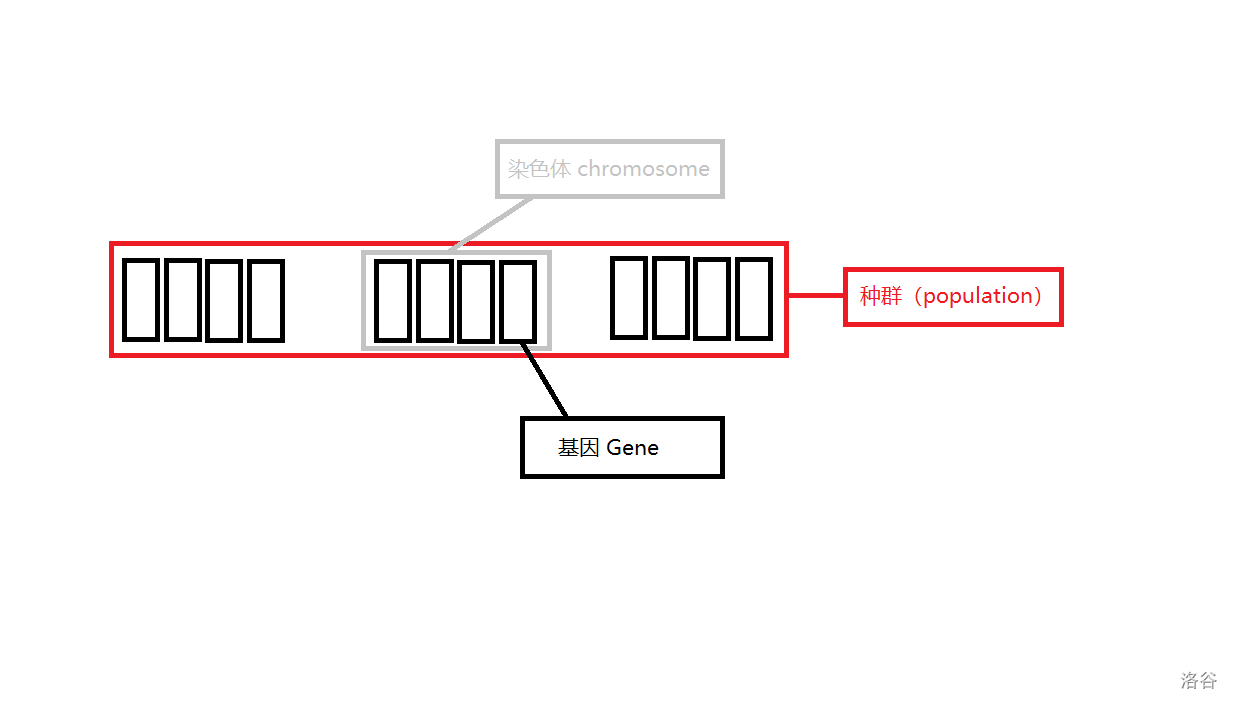
配图表示:
图中,种群、染色体、基因都已经标注上了。种群个体数量为
在算法中,我们对每个个体计算其染色体的适应度(
小试牛刀
尝试构建一个名字叫做
参考答案:
5|0遗传算法算子
1.交叉算子(
也有将该算子称为 因为第二种字数更少。
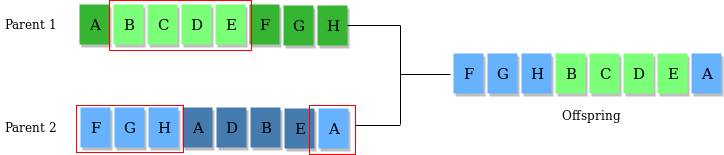
交叉算子就是模拟父母双方交配过程。想一想人类交配时,每个基因会随机的来自父亲或者母亲。我们可以模拟这个过程。假设我们的染色体用
当然,你也可以思考一些其他的交叉思路,比如随机抽取某些段进行交换。如下图所示:
(以上图片来自Genetic Algorithms)
这种算法通常在二进制条件下更加实用。
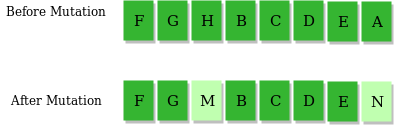
2.变异算子(
即低概率地随机地改变某个基因。这样可以有效避免程序陷入局部最优或者过慢收敛。例如:
一般来说,我们可以设计一个变异概率。变异率大概在
6|0遗传算法策略
- 精英保留策略
还是拿古人类举例。假设我们是上帝,我们想要古人类实现长久发展,最好的办法就是尽可能的将那些头脑敏捷,肢体强壮的个体保留下来,淘汰那些老弱病残的个体。
在程序中,我们将个体按照适应度排序,把适应度最好前
- 概率保留策略
学名好像是 Stoffa改进方法,这不重要。总之,就是为了避免父母生出傻孩子浪费时间,把傻孩子(适应度低的后代)直接抛弃。
假设我们要求收敛到最低适应度,后代适应度为
这个概率我们怎么来算呢?有一种方法给出了概率的计算函数:
其中
为什么是
为什么要用
下面放一张遗传算法求最短哈密尔顿路径的收敛图像。其中绿色实线是加了概率函数的,蓝色虚线则没有加。可以看出,绿色实现收敛的比较快,侧面证明了 Stoffa改进方法 的正确性。
思考题
如果我们要求最大适应值,那么概率的计算函数应当怎么计算呢?
答案:
7|0例题
7|1例题 1 : 牛刀小试
给定一个目标字符串(
比如从
这里先讲一下适应度函数的构造方法:比较当前染色体与目标字符串之间不同的字符个数即为适应度。显然,适应度越低越好。
上面都已经讲过了,这里直接贴出代码:
全部代码:
看一下输出结果:
7|2例题 2
题目描述
糖果店的老板一共有
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是
幸好糖果包装上注明了其中
给定
我知道可以用状压,但是这道题还可以用遗传!
考虑将品尝每包糖果的顺序作为染色体,适应度即为品尝过所有糖果需要购买的糖果包数的最小值。(这里指从头往后取)
注意,这里的适应度计算函数需要特别处理。由于染色体是个排列,我们直接交叉肯定会出现单个染色体内有许多基因重复。因此考虑“自交”,即用更高的变异概率代替双亲交配。
核心代码在这里:
7|3例题3
对于这道题来说,最重要的是设计一个适应度函数。显然地,我们可以将适应度函数设计为当前点到
在这道题里,染色体要设置成当前点的横纵坐标,这样怎么交配和变异呢?
首先先谈变异:我们可以将这个数写成二进制位,然后随机挑选一位取反。
对于交叉,我们可以使用原来的方法,也可以对于这个算法进行改进:为了避免答案精度过低,我们可以将父母双亲交配改成父代自交(也就是复制自己,随机变异几个点)产生后代。当然,我们会调高变异率。
代码如下,我加了部分注释:
- Q:为什么这里要存储二十位二进制呢?
- A:由于坐标范围在
7|4例题 4
这是不多的遗传算法能吊打模拟退火的题。
还是分为三部分来解决这道题:
-
染色体设计:显然,我们需要存储当前圆的圆心坐标、半径。
-
适应度函数(
-
交配函数(
写完以后交上去,你会惊喜的发现,这个算法收敛速度并不符合预期。因此需要一些奇特优化:
-
普通优化:玄学调参们。
-
奇技淫巧:我们发现对于位移向量
事实证明,这个优化力度及其大。轻松跑到了最优解。
代码如下:
7|5例题 5
给定
-
染色体设计(
-
适应度设计(
-
交配函数(
当参数分别为:
-
种群大小(
-
迭代次数(
-
初始温度(
-
步长为
即可通过本题。
7|6其他例题
基本上模拟退火能做的遗传都能搞。
物竞天择,适者生存。这是每个世界都适用的生存法则。
本文参考资料 Genetic Algorithms。
8|0后记
以下均为个人感想。不保证一定正确。
1.关于遗传算法和模拟退火算法的比较
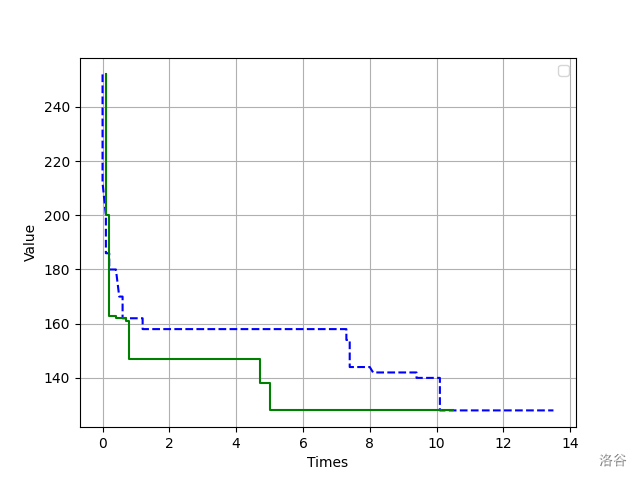
遗传算法的缺点就是收敛慢。对于求解最短哈密尔顿回路问题,遗传算法和模拟退火算法的表现如下(数据中
其中蓝色虚线是遗传算法,绿色实线是模拟退火算法。
可以看出,模拟退火算法收敛的很快,而遗传算法表现略逊。
实际上,在大部分问题上模拟退火表现都比遗传算法优秀得多。
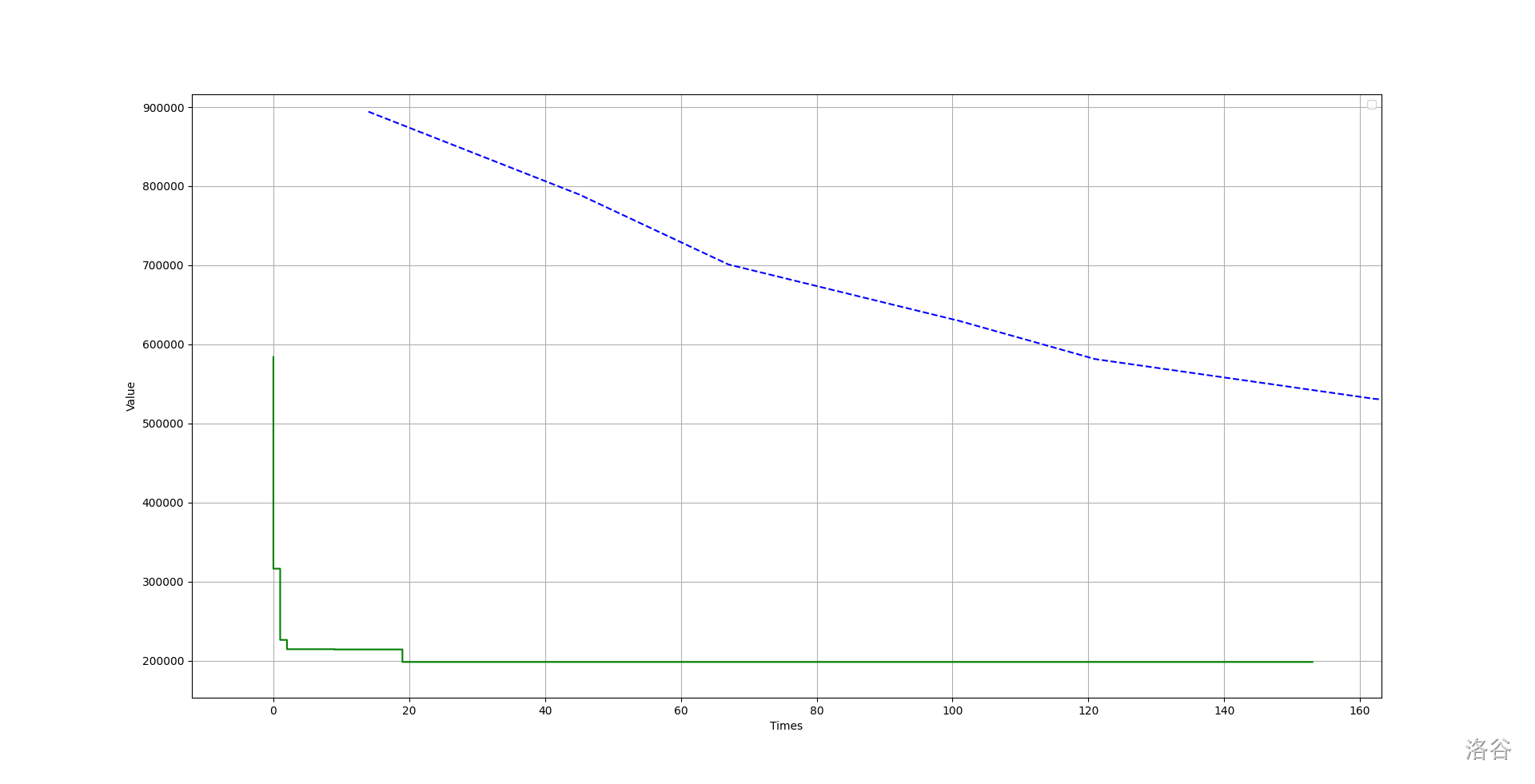
但是遗传算法在某些问题上还是有实践意义。对于某些数据量较大的情况,遗传算法更具有优势。还是拿刚才的求解哈密尔顿回路的问题举例。对于同一组数据,虽然模拟退火收敛较快而且在短时间内效果极好,但是在后期明显不如遗传算法。
2.对于 Stoffa 改进方法的概率接受
还是拿收敛到最低适应度举例。假设后代适应度为
其中
但是如果我们考虑一个极端情况:不妨先假设
其中这个
这种方法在模拟退火上同样可以应用,实测具有较好的优化效果。在其他网站上针对题目 UVA10228 A Star not a Tree? 进行测试,未进行优化需要跑
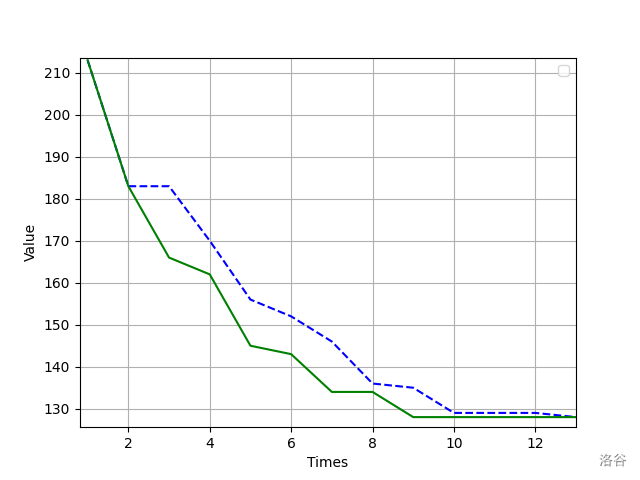
下面是对于求解
其中蓝色虚线使用的是没有改进的接受函数,而绿线使用的是改进后的接受函数。可以看出,的确存在一定的优化效果。
__EOF__

本文链接:https://www.cnblogs.com/kdlyh/p/17931201.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【.NET】调用本地 Deepseek 模型
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库