Codeforces Round 810 (Div. 2)

基本情况

A题秒了，B、C题死活看不懂题目。

B. Party

Problem - B - Codeforces

错误分析

为啥看不懂题目，一方面是英语水平确实不够，另一方面就是图的意识不行，如果能看出来这题隐含的建图思想，就很有助于理解题目。

---

正确思路

题意

有 \(T\) 组数据，每组数据给你一组 \(n, m\) 表示共有 \(n\) 个人，\(m\) 组朋友关系，及一个数组 \(a\) 和 \(m\) 组关系的具体值。其中 \(a_i\) 表示当第 \(i\) 人没有来参加聚会时，所带来的不快乐值。每对朋友会吃掉一个蛋糕。问在保证吃的蛋糕总数为偶数时，能达到的最小不快乐值。

转化

对于朋友关系及每个人，我们考虑建一个 \(n\) 个顶点，\(m\) 条边的无向图。其中的 \(n\) 个顶点分别为 \(1 \sim n\) 个人，\(m\) 条边为其中的 \(m\) 条朋友关系，即若两人有朋友关系，我们就在所建的图中编号对应的两点间连上一条无向边。

那么，问题就转换为了：

给出一个包含 \(n\) 个点 \(m\) 条边的图，及每个点的点权（\(a\) 数组）。删掉一些点和有关的边，使得图中有偶数条边。求删掉的点的点权总和最小值。

方法

我们分类讨论一下。

1. \(m\) 为偶数，则不需要删边或点，直接输出 \(0\) 即可。

2. \(m\) 为奇数，以下分三种情况讨论。

   1. 删一个点。显然，我们只能选择一个度为奇数的点。

   2. 删两个点。以下再分六种情况来讨论。

      1. 两点度数均为偶且有边，那么能够保证删除后边为偶数个，则两点均删除。
      2. 两点度数均为奇且有边，那么能够保证删除后边为偶数个，则两点均删除。
      3. 两点度数一奇一偶但无边，如下图。
         

      虽然能够保证删除后边为偶数个，但只删除其中的奇点 \(4\) 所获的不快乐值一定会更小，那么舍去这种情况。

      1. 对于上述三种情况下，若两点间有无边的条件相反的情况下，则删除后对边数的改变都是减少偶数条。如下图中删 \(1\)，\(4\) 或 \(5\)，\(7\) 或 \(3\)，\(4\) 号点，对边数变化为偶数无用，所以也舍去这三种情况。

      

   3. 删大于等于三个点。显然不会更优，也舍去（可以替换成只删一个或两个点的形式，不快乐值会更低）。

      如下图
      

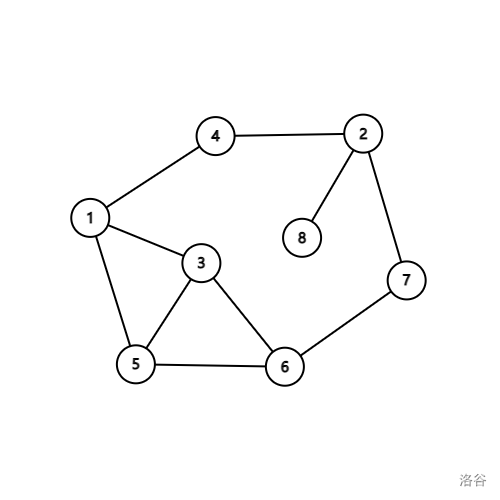
      若要删除 \(5\)，\(6\)，\(1\) 号顶点，我们可以替换为只删除 \(1\) 号点，也能使图中的边数边为偶数，且不快乐值更低。
      若要删除 \(1\)，\(2\)，\(3\)，\(4\) 号顶点，我们可以转化为只删除其中的任意一个奇点。

      • 而若要删除更多的点，我们只需要替换为只删一个或两个点就行。

代码

我们发现不用把图建出来，记录每个点的度数即可。

const int N = 1e5 + 10;
int n, m;
int d[N], a[N];
int u[N], v[N];

void solve()
{
	int ans = 0x7fffffff;
	std::cin >> n >> m;
	for (int i = 1; i <= n; i++) std::cin >> a[i], d[i] = 0;
	for (int i = 1; i <= m; i++) std::cin >> u[i] >> v[i], d[u[i]]++, d[v[i]]++;
	if ((m & 1) == 0) {std::cout << "0\n"; return ;}//边数为偶数
    //边数为奇数
	for (int i = 1; i <= n; i++) if (d[i] & 1) ans = ans < a[i] ? ans : a[i];//入读为奇数的点可以直接删除这一个点（等价于删了奇数条边，边数又能回到偶数）
	for (int i = 1; i <= m; i++) if ((d[u[i]] + d[v[i]] & 1) == 0) ans = ans < a[u[i]] + a[v[i]] ? ans : a[u[i]] + a[v[i]];//如上文讨论
	std::cout << ans << std::endl; 
}