Codeforces Round 801 (Div. 2)

1|0基本情况

A就开始犯病，导致+2.

B、C 都过样例了，但是都错。

2|0B. Circle Game

赛时推出来奇数必输，也知道偶数不是必赢，但是思路不清楚。

这里我没意识到一个很关键的性质。

奇数堆拿的石堆会变，这也导致了必输，比如三个堆 $1, 2, 3$ 。表粗的为JOE。

1 2 3 1 2 3

显然JOE拿的石堆是变化的。

偶数堆拿的石堆不会变！

1 2 3 4 1 2 3 4

通过分析，可以发现最小堆的石头（如果存在多个，我们取编号最小的）是第一个被拿完的，这堆石头的主人也必定会输。

那么偶数下直接看看最小堆是谁即可。

#include<iostream>
#include<algorithm>
#include<cstdio>

int a[51];

int main()
{
 	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cout.tie(nullptr);
	int _; std::cin >> _;
	while(_--)
	{
		int n, temp, ok = true, minP = 1;
		std::cin >> n;
		for(int i = 1; i <= n; i++) std::cin >> a[i];
		if (n & 1) {std::cout << "Mike" << std::endl; continue;}
		for (int i = 2; i <= n; i++)
		{
			if (a[i] < a[minP]) minP = i;
		}
		if (minP & 1) std::cout << "Joe" << std::endl;
		else std::cout << "Mike" << std::endl;
	}
	return 0;
}

3|0C. Zero Path

3|1我的错解

一眼DP，然后自以为是的写了一个逆天假DP。。。

dp[1][1] = a[1][1];
	dp[n][m] = 0x7fffffff; 
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if (i >= 2 && j == 1)
			{
				dp[i][j] = dp[i - 1][j] + a[i][j];continue;
			}
			if (j >= 2 && i == 1)
			{
				dp[i][j] = dp[i][j - 1] + a[i][j];continue;
			}
			if (abs(dp[i][j - 1] + a[i][j]) < abs(dp[i - 1][j] + a[i][j]) )
				dp[i][j] = dp[i][j - 1] + a[i][j];
			else
				dp[i][j] = dp[i - 1][j] + a[i][j];
		}
	std::cout << (dp[n][m] == 0 ? "YES" : "NO") << std::endl;

仔细一想，之前的题目，维护最大值、最小值，是符合DP的要求的，最优子结构，无后效性，虽然我说不明白，但是这题我维护的东西仔细想想并不符合DP的要求，所以这样直接维护是短视的，感觉有点像贪心，反正不是DP。

3|2正确DP

首先，如果经过奇数个格子，或者说 $n + m - 1$ 为奇数，那么肯定没有这样的一条路径（经过的 $- 1$ 和 $1$ 点没有办法相等）。

直接判断某个格子图是否符合要求太麻烦，我们可以思考，如果有任意一条路径，我们是否能根据这条路径的值（也就是途径的格子的和），来做一些改变，最后让路径的值变为 $0$ 。

如下图这样就是对路径做了一次改变（改变前后只有一个格子不同）。最后让路径的值产生了变化。

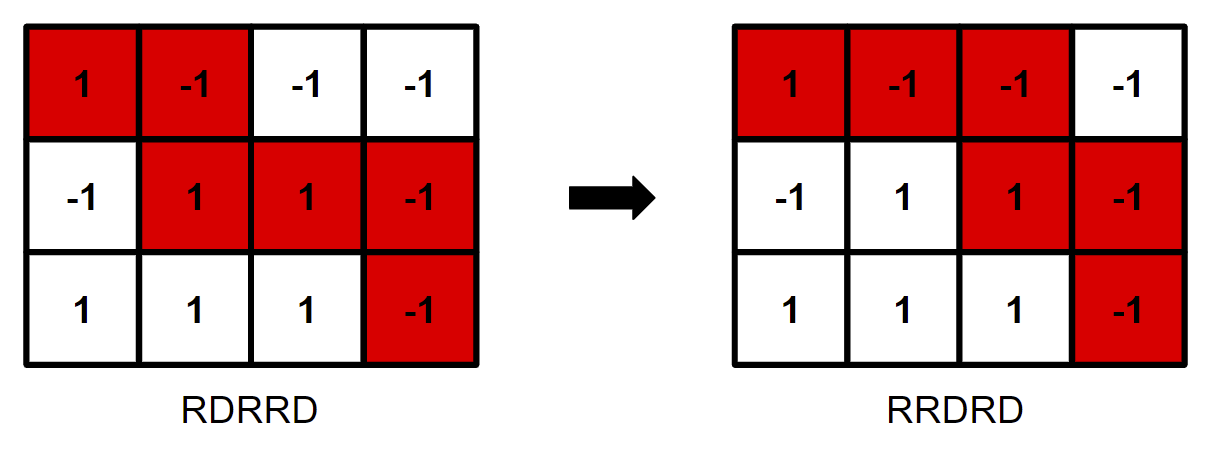
在一次改变中，路径的值会产生 $- 2 (- 1 \to 1)$ , $2 (1 \to - 1)$ 或是 $0 (1 \to 1 OR - 1 \to - 1)$ 的变化，那么如果我们刚开始的路径值是一个偶数，就可以把这个路径通过这样的改变变为 $0$ 吗？

显然是不行的，如果整个格点图全是 $- 1$ 或是全是 $1$ 就不行，所以我们还得做一些改进。

首先就得确保在这个格点图中不会只有值特别离谱的路径，如果只有值特别离谱的路径，那无论你怎么变，也搞不出值为 $0$ 的路径。

所以我们需要找出值最大的路径，以及值最小的路径。

设值最大的路径的值为 $p_{max}$ ，最小的路径的值为 $p_{min}$ 。

那么如果:

p_{min} \leq 0 \leq p_{max}

我们就一定可以通过这样的变化把任意一个值为偶数的路径变为值为 $0$ 的路径。

或者可以这样理解，如果符合上面那个条件，那我们就可以逐渐把值最小的路径向值最大的路径变换，在这个过程中，一定有一个路径的值等于 $0$ 。

至于求这样的格子图的最大和最小路径，就属于是典中典了。

4|0代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

const int N = 1e3 + 10;
int n, m;
int a[N][N];
int dp1[N][N], dp2[N][N];

void solve()
{
	std::cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) std::cin >> a[i][j];
	memset(dp2, 0, sizeof(dp2));
	memset(dp1, 0, sizeof(dp1));
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if (i >= 2 && j == 1)
			{
				dp1[i][j] = dp1[i - 1][j] + a[i][j]; dp2[i][j] = dp2[i - 1][j] + a[i][j]; 
				continue;
			}
			if (j >= 2 && i == 1)
			{
				dp1[i][j] = dp1[i][j - 1] + a[i][j]; dp2[i][j] = dp2[i][j - 1] + a[i][j]; 
				continue;
			}
			dp1[i][j] = std::max(dp1[i - 1][j], dp1[i][j - 1]) + a[i][j];
			dp2[i][j] = std::min(dp2[i - 1][j], dp2[i][j - 1]) + a[i][j]; 
		}
	if (dp1[n][m] & 1 || dp2[n][m] > 0 || dp1[n][m] < 0) 
	{
        std::cout << "NO\n";
    } 
	else
	{
        std::cout << "YES\n";
    }
} 

int main()
{
 	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cout.tie(nullptr);
	int _; std::cin >> _;
	while(_--) solve();
	return 0;
}

__EOF__

本文作者：Kdlyh
本文链接：https://www.cnblogs.com/kdlyh/p/17891381.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！