“扩展域”与“边带权”的并查集
其实之前并查集题单都做到过,但是并没有针对性的总结为类型题。
引入
并查集擅长维护具有传递性的关系及其连通性。在某些问题中,“传递关系”不止一种,并且这些”传递关系“能够互相导出。此时就可以使用”扩展域“或”边带权“并查集来解决。
[NOI2002] 银河英雄传说
题目描述
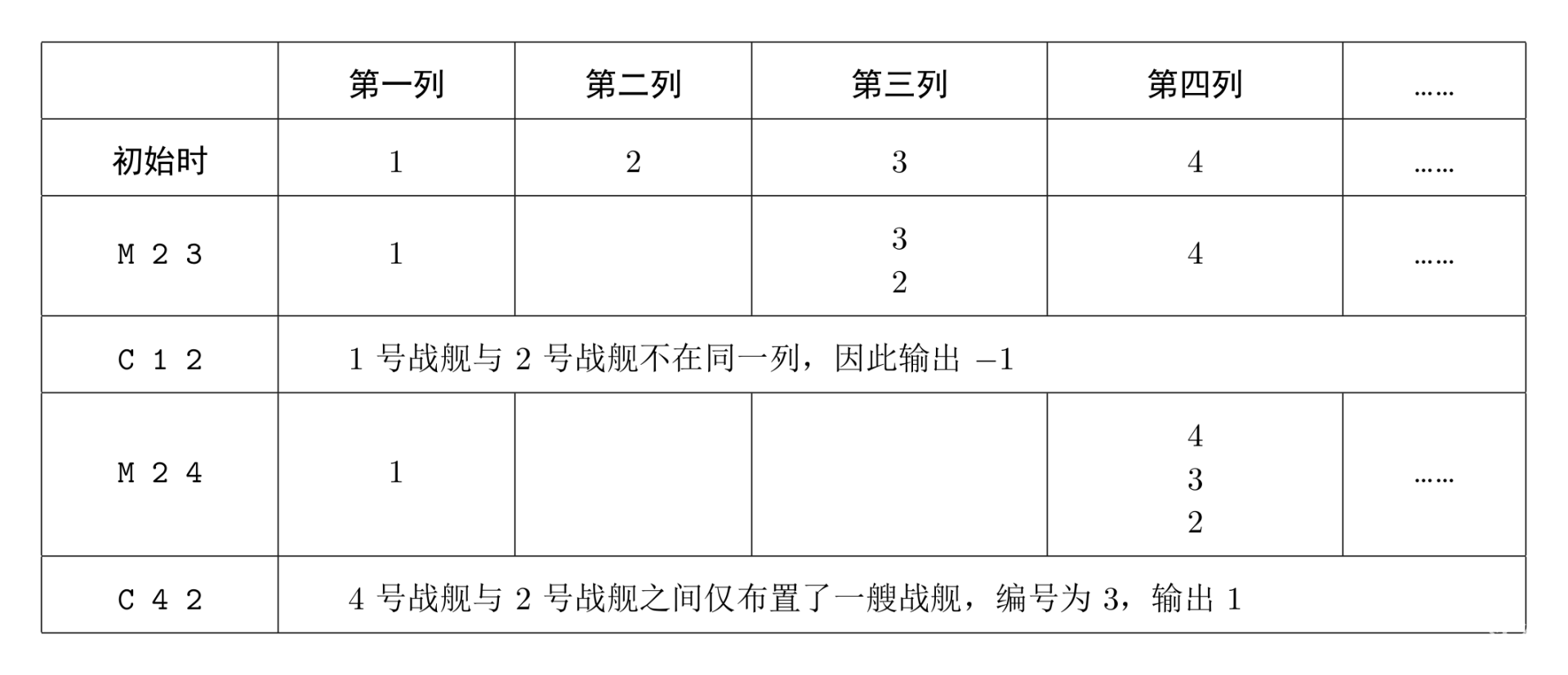
杨威利擅长排兵布阵,巧妙运用各种战术屡次以少胜多,难免恣生骄气。在这次决战中,他将巴米利恩星域战场划分成 \(30000\) 列,每列依次编号为 \(1, 2,\ldots ,30000\)。之后,他把自己的战舰也依次编号为 \(1, 2, \ldots , 30000\),让第 \(i\) 号战舰处于第 \(i\) 列,形成“一字长蛇阵”,诱敌深入。这是初始阵形。当进犯之敌到达时,杨威利会多次发布合并指令,将大部分战舰集中在某几列上,实施密集攻击。合并指令为 M i j,含义为第 \(i\) 号战舰所在的整个战舰队列,作为一个整体(头在前尾在后)接至第 \(j\) 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。
然而,老谋深算的莱因哈特早已在战略上取得了主动。在交战中,他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。
在杨威利发布指令调动舰队的同时,莱因哈特为了及时了解当前杨威利的战舰分布情况,也会发出一些询问指令:C i j。该指令意思是,询问电脑,杨威利的第 \(i\) 号战舰与第 \(j\) 号战舰当前是否在同一列中,如果在同一列中,那么它们之间布置有多少战舰。
作为一个资深的高级程序设计员,你被要求编写程序分析杨威利的指令,以及回答莱因哈特的询问。
输入格式
第一行有一个整数 \(T\)(\(1 \le T \le 5 \times 10^5\)),表示总共有 \(T\) 条指令。
以下有 \(T\) 行,每行有一条指令。指令有两种格式:
M i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令,并且保证第 \(i\) 号战舰与第 \(j\) 号战舰不在同一列。C i j:\(i\) 和 \(j\) 是两个整数(\(1 \le i,j \le 30000\)),表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。
输出格式
依次对输入的每一条指令进行分析和处理:
- 如果是杨威利发布的舰队调动指令,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息。
- 如果是莱因哈特发布的询问指令,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 \(i\) 号战舰与第 \(j\) 号战舰之间布置的战舰数目。如果第 \(i\) 号战舰与第 \(j\) 号战舰当前不在同一列上,则输出 \(-1\)。
样例 #1
样例输入 #1
4
M 2 3
C 1 2
M 2 4
C 4 2
样例输出 #1
-1
1
提示
样例解释
战舰位置图:表格中阿拉伯数字表示战舰编号。
边带权并查集
概念
并查集实际上是由若干棵树组成的森林:
- 我们可以在树中的每条边上记录一个权值,即维护一个数组 \(d\),用 \(d_x\) 保存节点 \(x\) 到父节点 \(fa_x\) 之间的边权。
- 在每次路径压缩后,每个访问后的节点都会直接指向树根,如果我们同时更新这些节点的 \(d\) 值,就可以利用路径压缩的过程来统计每个节点到树根之间的路径上的一些信息。
思路
一条“链”也是一棵树,只不过是树的特殊形态。因此可以把每一列战舰看作一个集合,用并查集维护。最初,\(N\) 个战舰构成独立的 \(N\) 个集合。
在没有路径压缩的情况下,\(fa_x\) 就表示排在第 \(x\) 号战舰前面的那个战舰的编号。一个集合的代表就是位于最前面的那个战舰。另外,让树上每条边带权值 \(1\),这样树上两点之间的距离减 \(1\) 就是两者之间间隔战舰的数量。
在考虑路径压缩的情况下,我们额外建立一个数组 \(d\),\(d_x\) 记录战舰 \(x\) 与 \(fa_x\) 之间的边的权值。在路径压缩把 \(x\) 直接指向树根的同时,我们把 \(d_x\) 更新为从 \(x\) 到树根路径上所有边权之和。下面的代码对 \(\operatorname {get}\) 函数稍加修改,即可实现对 \(d\) 数组的维护。
int get(int x)
{
if (x == fa[x]) return x;
int root = get(fa[x]);
d[x] += d[fa[x]];
return fa[x] = root;
}
当接收到一个 \(C\space x\space y\) 指令时,分别执行 \(\operatorname {get}(x)\) 和 \(\operatorname {get}(y)\) 完成查询和路径压缩。若二者的返回值相同,则说明 \(x\) 和 \(y\) 处于同一列中。
因为此时 \(x\) 和 \(y\) 都已经指向树根,所以 \(d_x\) 保存了位于 \(x\) 之前的战舰数量, \(d_y\) 保存了位于 \(y\) 之前的战舰数量。二者之差的绝对值再减 \(1\),就是 \(x\) 和 \(y\) 之间间隔的战舰数量。
当接收到一个 \(M\space x\space y\) 指令时,把 \(x\) 的树根作为 \(y\) 的树根的字节点,连接新边的权值应该设为合并之前集合 \(y\) 的大小(根据题意,集合 \(y\) 中全部战舰都排在集合 \(x\) 之前)。因此,我们还需要一个 \(size\) 数组在每个树根上记录集合大小。下面这段对 \(\operatorname {merge}\) 函数稍加修改的代码实现了这条命令:
void merge(int x, int y)
{
x = get(x), y = get(y);
fa[x] = y, d[x] = size[y];
size[y] += size[x];
}
AC代码
#include<iostream>
#include<algorithm>
#include<cstdio>
const int N = 30000 + 10;
int fa[N], d[N], size[N];
void init()
{
for (int i = 1; i <= 30000; i++) fa[i] = i, size[i] = 1;
return ;
}
int get(int x)
{
if (x == fa[x]) return x;
int root = get(fa[x]);
d[x] += d[fa[x]];
return fa[x] = root;
}
void merge(int x, int y)
{
x = get(x), y = get(y);
fa[x] = y, d[x] = size[y];
size[y] += size[x]; size[x] = 0;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _; std::cin >> _;
init();
while(_--)
{
char opt; int x, y;
std::cin >> opt >> x >> y;
if (opt == 'C')
{
if (get(x) == get(y))
{
std::cout << abs(d[x] - d[y]) - 1;
}
else
{
std::cout << -1;
}
std::cout << std::endl;
}
else
{
merge(x, y);
}
}
return 0;
}
[POJ1733] Parity game
小 A 和小 B 在玩一个游戏。
首先,小 A 写了一个由 0 和 1 组成的序列 S,长度为 N。
然后,小 B 向小 A 提出了 M 个问题。
在每个问题中,小 B 指定两个数 l 和 r,小 A 回答 \(S[l∼r]\) 中有奇数个 1 还是偶数个 1。
机智的小 B 发现小 A 有可能在撒谎。
例如,小 A 曾经回答过 \(S[1∼3]\) 中有奇数个 1,\(S[4∼6]\) 中有偶数个 1,现在又回答 \(S[1∼6]\) 中有偶数个 1,显然这是自相矛盾的。
请你帮助小 B 检查这 M 个答案,并指出在至少多少个回答之后可以确定小 A 一定在撒谎。
即求出一个最小的 k,使得 01 序列 S 满足第 \(1∼k\) 个回答,但不满足第 \(1∼k+1\) 个回答。
输入格式
第一行包含一个整数 N,表示 01 序列长度。
第二行包含一个整数 M,表示问题数量。
接下来 M 行,每行包含一组问答:两个整数 l 和 r,以及回答 even 或 odd,用以描述 \(S[l∼r]\) 中有偶数个 1 还是奇数个 1。
输出格式
输出一个整数 k,表示 01 序列满足第 \(1∼k\) 个回答,但不满足第 \(1∼k+1\) 个回答,如果 01 序列满足所有回答,则输出问题总数量。
数据范围
\(N\leq10^9,M\leq5000\)
输入样例:
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd
输出样例:
3
分析
如果用 \(sum\) 数组来表示序列 \(S\) 的前缀和,那么在每个回答中:
- $S[1\sim r] $ 中有偶数个 \(1\),等价于 \(sum_{l-1}\) 与 \(sum_r\) 奇偶性相同。
- $S[1\sim r] $ 中有奇数个 \(1\),等价于 \(sum_{l-1}\) 与 \(sum_r\) 奇偶性不同。
注意,这里没有求出 \(sum\) 数组,我们只是把 \(sum\) 看作变量。可以发现,这与P1955 [NOI2015] 程序自动分析非常相似:
都是给定若干个变量和关系,判定这些关系可满足性的问题。只是本题的传递关系不止一种:
- 若 \(x_1\) 与 \(x_2\) 的奇偶性相同, \(x_2\) 与 \(x_3\) 的奇偶性也相同,那么 \(x_1\) 与 \(x_3\) 奇偶性相同。这种情况与 P1955 [NOI2015] 程序自动分析 中的等同关系一样。
- 若 \(x_1\) 与 \(x_2\) 的奇偶性相同, \(x_2\) 与 \(x_3\) 的奇偶性不相同,那么 \(x_1\) 与 \(x_3\) 奇偶性不同。
- 若 \(x_1\) 与 \(x_2\) 的奇偶性不同, \(x_2\) 与 \(x_3\) 的奇偶性也不同,那么 \(x_1\) 与 \(x_3\) 奇偶性相同。
另外,序列长度 \(N\) 很大,但问题数 \(M\) 很小,可以用离散化把每个问题的两个整数 \(l-1\) 和 \(r\) 缩小到等价的 \(1\sim 2M\) 以内的范围。
struct {int l, r, ans;}query[10010];
int a[20010], fa[20010], d[20010], n, m, t;
void read_discrete()//读入、离散化
{
std::cin >> n >> m;
for (int i = 1; i <= m; i++)
{
char str[5];
scanf(%d%d%s, &query[i].l, &query[i].r, str);
query[i].ans = (str[0] == 'o' ? 1 : 0);
a[++t] = query[i].l - 1;
a[++t] = query[i].r;
}
std::sort(a + 1, a + t + 1);
n = std::unique(a + 1, a + t + 1) - a - 1;
}
“边带权” 的并查集
- 边权 \(d_x\) 为 \(0\) ,表示 \(x\) 与 \(fa_x\) 奇偶性相同。
- 边权 \(d_x\) 为 \(1\) ,表示 \(x\) 与 \(fa_x\) 奇偶性不同。
在路径压缩时,对 \(x\) 到树根路径上的所有边权做异或运算(不同为 \(1\),相同为 \(0\)),即可得到 \(x\) 与树根的奇偶性关系。
对于每个问题,设在离散化后 \(l-1\) 和 \(r\) 的值分别是 \(x\) 和 \(y\),设 \(ans\) 表示该问题的回答(\(0\) 代表偶数个,\(1\) 代表奇数个)。
先检查 \(x\) 和 \(y\) 是否在同一个集合内(奇偶性关系是否已知)。
\(\texttt{get}(x)\)、\(\texttt{get}(y)\) 都执行完成后,\(d_x \oplus d_y\) 即为 \(x\) 和 \(y\) 的奇偶关系。若 \(d_x \oplus d_y \neq ans\),则在该问题之后可以确定小 \(A\) 在撒谎。
若 \(x\) 和 \(y\) 不在一个集合内,则合并两个集合。此时应该先通过 \(\texttt{get}\) 操作得到两个集合的树根(设为 \(p\) 和 \(q\)),令 \(p\) 为 \(q\) 的子节点。
- 已知 \(d_x\) 与 \(d_y\) 分别表示路径 \(x\sim p\) 与 \(y\sim q\) 之间所有边权的异或和,而 \(p\sim q\) 之间的边权 \(d_p\) 是待求的值。
- 显然,路径 \(x\sim y\) 由路径 \(x\sim p\),\(p\sim q\) 与 \(q\sim y\) 组成
- 因此 \(x\) 与 \(y\) 的奇偶性关系 \(ans = d_x\oplus d_y\oplus d_y\)。
- 进而推出新连接的边权 \(d_p = d_x\oplus d_y\oplus ans\)
#include<iostream>
#include<algorithm>
#include<cstdio>
const int N = 1e5 + 10;
struct {int l, r, ans;}query[5010];
int a[N], fa[N], d[N], n, m, t;
void read_discrete()
{
std::cin >> n >> m;
for (int i = 1; i <= m; i++)
{
char str[5];
scanf("%d%d%s", &query[i].l, &query[i].r, str);
query[i].ans = (str[0] == 'o' ? 1 : 0);
a[++t] = query[i].l - 1;
a[++t] = query[i].r;
}
std::sort(a + 1, a + t + 1);
n = std::unique(a + 1, a + t + 1) - a - 1;
}
int get(int x)
{
if (x == fa[x]) return x;
int root = get(fa[x]);//这一步除了求出祖先是谁之外,也维护了d[fa[x]],才能进行下一步
d[x] ^= d[fa[x]];
return fa[x] = root;
}
int main()
{
read_discrete();
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= m; i++)
{
//求出 l-1 和 r 离散化之后的值
int x = std::lower_bound(a + 1, a + n + 1, query[i].l - 1) - a;
int y = std::lower_bound(a + 1, a + n + 1, query[i].r) - a;
int p = get(x), q = get(y);
//执行get函数,得到树根,并进行路径压缩
if (p == q)//已经在同一集合内
{
if ((d[x] ^ d[y]) != query[i].ans)
{std::cout << i - 1 << std::endl; return 0;}
}
else//不在同一集合,合并
fa[p] = q, d[p] = d[x] ^ d[y] ^ query[i].ans;
}
std::cout << m << std::endl;//没有矛盾
return 0;
}
“扩展域” 的并查集
把每个变量 \(x\)(即离散化后的 \(l-1\) )拆成两个节点 \(x_{odd}\) 和 \(x_{even}\),其中 \(x_{odd}\) 表示 \(sum_x\) 是奇数,\(x_{even}\) 表示 \(sum_x\) 是偶数。也可以叫做 \(x\) 的奇数域、偶数域。\(y\) (离散化后的 \(r\))同理。
int fa[N << 1];
int x_odd = x, x_even = x + n;
int y_odd = y, y_even = y + n;//利用向后移n个节点来保证不会相互影响,并查集大小记得开两倍
对于每个问题,设在离散化后 \(l-1\) 和 \(r\) 的值分别是 \(x\) 和 \(y\),设 \(ans\) 表示该问题的回答(\(0\) 代表偶数个,\(1\) 代表奇数个)。
- 若 \(ans = 0\),则合并 \(x_{odd}\) 与 \(y_{odd}\),\(x_{even}\) 与 \(y_{even}\)。这表示两个信息:
- “x为奇数”与“y为奇数”可以互相推出。
- “x为偶数”与“y为偶数”可以互相推出。
- 它们是等价的信息。
- 若 \(ans = 1\),则合并 \(x_{odd}\) 与 \(y_{even}\),\(x_{even}\) 与 \(y_{old}\)。这表示两个信息:
- “x为奇数”与“y为偶数”可以互相推出。
- “x为偶数”与“y为奇数”可以互相推出。
- 它们是等价的信息。
上述合并同时还维护了关系的传递性。试想,在处理完 \((x,y,0)\) 和 \((y,z,1)\) 两个回答之后,\(x\) 和 \(z\) 之间的关系也就已知了,这种做法就相当于在无向图上维护节点之间的联通情况,只是扩展了多个域来应对多种传递关系。
在处理每个问题之前,当然要先检查是否存在矛盾。
- 若两个变量 \(x\) 和 \(y\) 对应的 \(x_{odd}\) 和 \(y_{odd}\) 节点在同一集合内,则二者奇偶性应该相同。
- 若两个变量 \(x\) 和 \(y\) 对应的 \(x_{odd}\) 和 \(y_{even}\) 节点在同一集合内,则二者奇偶性应该不同。
#include<iostream>
#include<algorithm>
#include<cstdio>
const int N = 1e5 + 10;
struct {int l, r, ans;}query[5010];
int a[N<<1], fa[N<<1], n, m, t;
void read_discrete()
{
std::cin >> n >> m;
for (int i = 1; i <= m; i++)
{
char str[5];
scanf("%d%d%s", &query[i].l, &query[i].r, str);
query[i].ans = (str[0] == 'o' ? 1 : 0);
a[++t] = query[i].l - 1;
a[++t] = query[i].r;
}
std::sort(a + 1, a + t + 1);
n = std::unique(a + 1, a + t + 1) - a - 1;
}
int get(int x)
{
if (x == fa[x]) return x;
return fa[x] = get(fa[x]);
}
int main()
{
read_discrete();
for (int i = 1; i <= n<<1; i++) fa[i] = i;
for (int i = 1; i <= m; i++)
{
//求出 l-1 和 r 离散化之后的值
int x = std::lower_bound(a + 1, a + n + 1, query[i].l - 1) - a;
int y = std::lower_bound(a + 1, a + n + 1, query[i].r) - a;
int x_odd = x, x_even = x + n;
int y_odd = y, y_even = y + n;
if (query[i].ans == 0)//回答奇偶性相同
{
if (get(x_odd) == get(y_even))//与已知情况矛盾
{
std::cout << i - 1 << std::endl;
return 0;
}
fa[get(x_odd)] = get(y_odd);//合并
fa[get(x_even)] = get(y_even);
}
else
{
if (get(x_odd) == get(y_odd))//与已知情况矛盾
{
std::cout << i - 1 << std::endl;
return 0;
}
fa[get(x_odd)] = get(y_even);//合并
fa[get(x_even)] = get(y_odd);
}
}
std::cout << m << std::endl;//没有矛盾
return 0;
}
P2024 [NOI2001] 食物链
题目描述
动物王国中有三类动物 \(A,B,C\),这三类动物的食物链构成了有趣的环形。\(A\) 吃 \(B\),\(B\) 吃 \(C\),\(C\) 吃 \(A\)。
现有 \(N\) 个动物,以 \(1 \sim N\) 编号。每个动物都是 \(A,B,C\) 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 \(N\) 个动物所构成的食物链关系进行描述:
- 第一种说法是
1 X Y,表示 \(X\) 和 \(Y\) 是同类。 - 第二种说法是
2 X Y,表示 \(X\) 吃 \(Y\)。
此人对 \(N\) 个动物,用上述两种说法,一句接一句地说出 \(K\) 句话,这 \(K\) 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 \(X\) 或 \(Y\) 比 \(N\) 大,就是假话;
- 当前的话表示 \(X\) 吃 \(X\),就是假话。
你的任务是根据给定的 \(N\) 和 \(K\) 句话,输出假话的总数。
输入格式
第一行两个整数,\(N,K\),表示有 \(N\) 个动物,\(K\) 句话。
第二行开始每行一句话(按照题目要求,见样例)
输出格式
一行,一个整数,表示假话的总数。
样例 #1
样例输入 #1
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
样例输出 #1
3
提示
对于全部数据,\(1\le N\le 5 \times 10^4\),\(1\le K \le 10^5\)。
“扩展域”并查集解法
构造扩展域并查集
把每个动物 \(x\) 拆分为三个节点:
- 同类域 \(x_{self}\)
- 捕食域 \(x_{eat}\)
- 天敌域 \(x_{enemy}\)
若一句话说“\(x\) 与 \(y\) 是同类”,则说明:
- \(x\) 的同类与 \(y\) 的同类一样。
- \(x\) 捕食的物种与 \(y\) 的捕食的物种一样。
- \(x\) 的天敌与 \(y\) 的天敌一样。
此时,我们应合并 \((x_{self},y_{self})\)、\((x_{eat},y_{eat})\),\((x_{enemy},y_{enemy})\)。
若一句话说“\(x\) 吃 \(y\) ”,则说明:
- \(x\) 捕食的物种 就是 \(y\) 的同类。
- \(x\) 的同类 都是 \(y\) 的天敌。
- 又因为题目说食物链是长度为 \(3\) 的环形,所以 \(x\) 的天敌 就是 \(y\) 捕食的物种。
此时,我们应合并 \((x_{eat},y_{self})\)、\((x_{self},y_{enemy})\),\((x_{enemy},y_{eat})\)。
在处理每句话之前,都要检验这句话的真假:
与“\(x\) 与 \(y\) 是同类”矛盾的信息:
- \(x_{eat}\) 与 \(y_{self}\) 在同一集合,说明 \(x\) 吃 \(y\)。
- \(y_{eat}\) 与 \(x_{self}\) 在同一集合,说明 \(y\) 吃 \(x\)。
与“\(x\) 吃 \(y\) ”矛盾的信息:
- \(x_{self}\) 与 \(y_{self}\) 在同一集合,说明 \(x\) 与 \(y\) 是同类。
- \(x_{self}\) 与 \(y_{eat}\) 在同一集合,说明 \(y\) 吃 \(x\)。
代码实现
#include<iostream>
#include<algorithm>
#include<cstdio>
const int N = 5e4 + 10;
int fa[N * 3];
int n, k;
int get(int x)
{
return fa[x] == x ? x : fa[x] = get(fa[x]);
}
void merge(int fx, int fy)
{
fa[fx] = fy;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::cin >> n >> k;
for (int i = 1; i <= n * 3; i++) fa[i] = i;
int cnt = 0;
for (int i = 1; i <= k; i++)
{
int opt, x, y;
std::cin >> opt >> x >> y;
int x_self = x, x_eat = x + n, x_enemy = x + n * 2;
int y_self = y, y_eat = y + n, y_enemy = y + n * 2;
int fx_self = get(x_self), fx_eat = get(x_eat), fx_enemy = get(x_enemy);
int fy_self = get(y_self), fy_eat = get(y_eat), fy_enemy = get(y_enemy);
if (x > n || y > n) {++cnt; continue;}
if (opt == 1)
{
if (fx_eat == fy_self || fx_self == fy_eat) cnt++;
else {merge(fx_self, fy_self); merge(fx_eat, fy_eat); merge(fx_enemy, fy_enemy);}
}
else
{
if (fx_self == fy_self || fx_self == fy_eat) cnt++;
else {merge(fx_self, fy_enemy); merge(fx_eat, fy_self); merge(fx_enemy, fy_eat);}
}
}
std::cout << cnt;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号