前端的几种基本算法(二分查找,选择排序,插入排序,希尔排序,归并排序,快速排序,堆排序)
现在前端对于算法的要求是越来越高了,以下简单归纳下前端的几种基本的排序算法与二分查找相关的内容
二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
在有序的数组中查询一个元素用二分查找法是非常高效的,在应用中可以简单的分为三种情况,即:查找目标值,查找比目标值大的第一个元素,查找比目标值小的第一个元素。
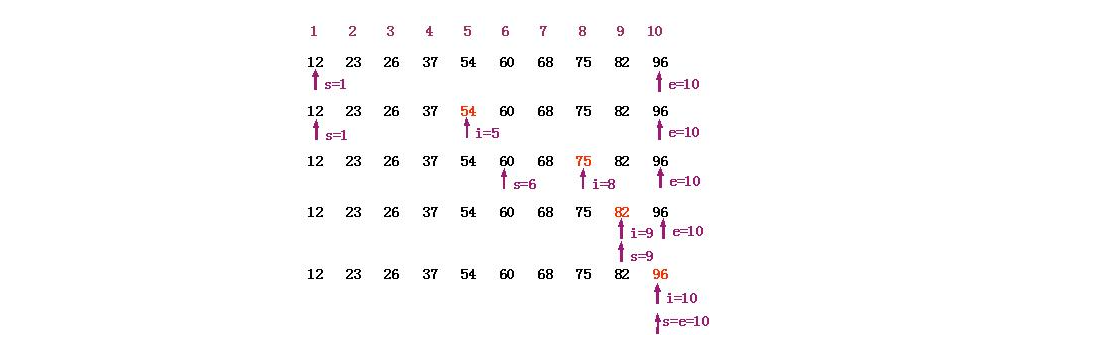
查找目标值
function binarySearch(arr, target) { let l = 0 let r = arr.length - 1 let mid = 0 while(l <= r) { mid = (l + r) >> 1 if (arr[mid] > target) { r = mid - 1 } else if (arr[mid] < target) { l = mid + 1 } else { return mid } } return -1 }
查找比目标值大的第一个元素
function binarySearchFirstGreate(arr, target) { let l = 0 let r = arr.length - 1 let mid = 0 while(l <= r) { mid = (l + r) >> 1 if (arr[mid] > target) { r = mid - 1 } else { l = mid + 1 } } return l }
查找比目标值小的第一个元素
function binarySearchFirstLess(arr, target) { let l = 0 let r = arr.length - 1 let mid = 0 while(l <= r) { mid = (l + r) >> 1 if (arr[mid] < target) { l = mid + 1 } else { r = mid - 1 } } return r }
选择排序
选择排序的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
选择排序是不稳定的排序方法。

function selectionSort(arr) { let l = arr.length for(let i = 0; i < l; i++) { for(let j = i + 1; j < l; j++) { if (arr[i] > arr[j]) { [arr[i], arr[j]] = [arr[j], arr[i]] } } } }
插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。
插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动
它与选择排序的区别是:
- 选择排序是在未排列的数据中选取最大(小)的值。
- 插入排序是在已排列的数据中寻找正确的位置,所以插入排序比选择排序性能会好很多。

function insertSort(arr) { let l = arr.length for(let i = 1; i < l; i++) { for(let j = i; j > 0; j--) { if (arr[j - 1] > arr[j]) { [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]] } } } }
希尔排序(增强版的插入排序)
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止。
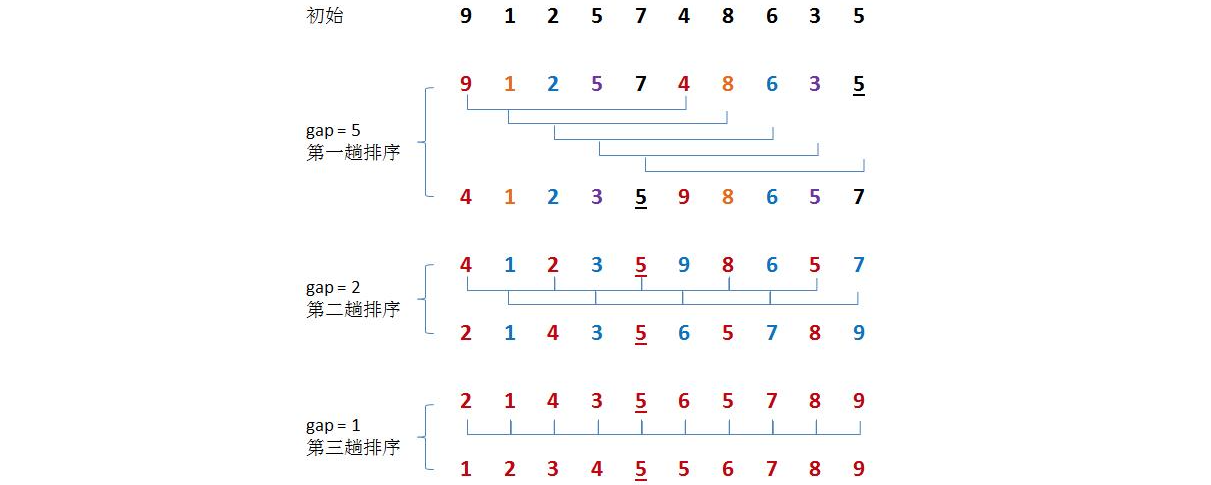
function shellSort(arr) { let t = new Date() let len = arr.length let h = 1 while(h < len / 3) h = 3 * h + 1 // 1, 4, 13, 40, 121, 364, 1093 while(h >= 1) { // 将数组变为h有序 for(let i = h; i < len; i++) { for(let j = i; j >= h; j -= h) { if (arr[j] < arr[j - h]) { [arr[j - h], arr[j]] = [arr[j], arr[j - h]] } } } h = Math.floor(h / 3) } }
归并排序
归并排序(Merge Sort)是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。

首先归并排序需要一个将两个有序数组合并的方法:
function merge(a, l, m, r) { let i = l, j = m + 1, aux = [] for (let k = l;k <= r; k++) { aux[k] = a[k] } for (let k = l; k <= r; k++) { if (i > m) { a[k] = aux[j++] } else if (j > r) { a[k] = aux[i++] } else if (aux[j] < aux[i]) { a[k] = aux[j++] } else { a[k] = aux[i++] } } return a }
归并排序的算法可以分为两种方式:
-
自顶向下:采用递归的方式,不断的将分割的子数组,直到将子数组的个数分割成1,然后再用merge合并成一个有序的大数组
-
自底向上:采用双层循环的方式,先将数组内的元素与相邻元素归并,然后递增到最后的一个大数组
自顶向下
function sort_down(a, l, r) { if (l >= r) return let m = (l + r) >> 1 sort_down(a, l, m) // 左边排序 sort_down(a, m + 1, r) // 右边排序 if (a[m] > a[m + 1]) { merge(a, l, m, r) // 合并 } }
自底向上
function sort_up(a) { let n = a.length for (let i = 1; i < n; i += i) { for (let j = 0; j < n - i; j += i + i) { merge(a, j, i + j - 1, Math.min(j + i + i - 1, n - 1)) } } }
快速排序
快速排序(Quicksort)是对冒泡排序算法的一种改进。
快速排序是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速的原地排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序分为两种方式:
- 二向切分快速排序:先进行左指针的值与base的比较,如果比base大,则从右指针递减与base的比较,如果遇到比base小的则进行左指针与右指针互换,以此规则循环,直到比base小的都在左,大的都在右。然后进行递归直到整个数组有序。
- 三向切分快速排序:设立三个指针:左指针,中指针,右指针。三向切分只比较中指针指向的值与base的大小,如果中指针小于base,则左指针与中指针互换且都递增1,如果比base大,则中指针与右指针互换,继续与base比较,如果相等,则中指针加1,直到整个数组的左部分都比base小,右部分都比base大,然后递归直到整个数组有序。(左指针的索引是与base最近的,直到右指针的索引靠近base,则该循环结束。)
三向切分比二向切分的优化点在于:如果数组能有重复值的话,三向切分不需要重复比较,而二向切分是要重复比较的,对于大批量的用户数据排序,该特性非常有用。
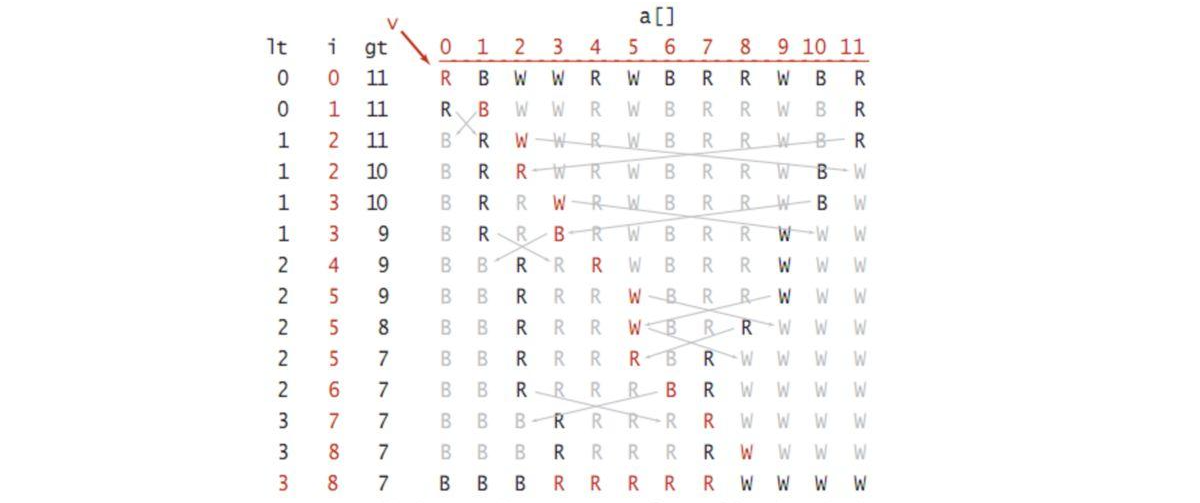
三向切分图
二向切分快速排序
function quickSort(arr, l, r) { if (l >= r) return let base = arr[l] let i = l let j = r while(l <= r) { while(l < r && arr[++l] < base) {} while(l < r && arr[--r] > base) {} if (l < r) { [arr[l], arr[r]] = [arr[r], arr[l]] } else { [arr[l - 1], arr[i]] = [base, arr[l - 1]] break } } quicksort(arr, i, l - 2) quicksort(arr, l, j) }
三向切分快速排序
function sQuickSort(arr, l, r) { if (l >= r) return let lf = l let ri = r let v = arr[lf] let i = l + 1 while(i <= ri) { if (v > arr[i]) { [arr[lf++], arr[i++]] = [arr[i], arr[lf]] } else if (v < arr[i]) { [arr[i], arr[ri--]] = [arr[ri], arr[i]] } else { i++ } } squicksort(arr, l, lf - 1) squicksort(arr, ri + 1, r) }
堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
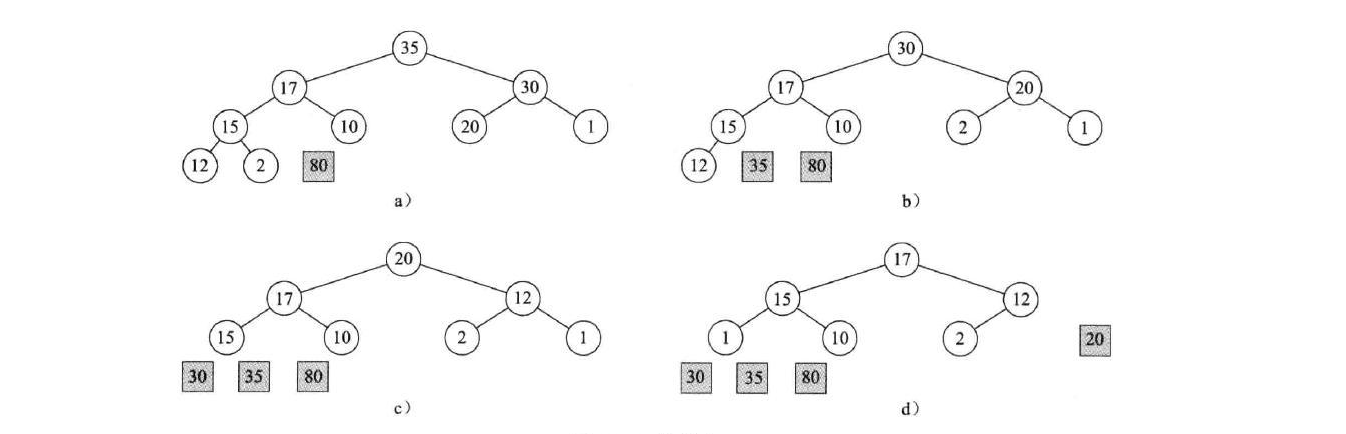
堆有两个重要的基本操作,即在堆有序时对单个元素的下沉和上浮操作。
以大顶堆为例(大顶堆即堆顶元素为最大,小顶堆的堆顶元素为最小):
大顶堆的下沉:
function sink(arr, k, len) { while(2 * k + 1 < len) { let j = 2 * k + 1 if (j < len - 1 && arr[j] < arr[j + 1]) j++ if (arr[k] >= arr[j]) break [arr[k], arr[j]] = [arr[j], arr[k]] k = j } }
大顶堆的上浮:
function swim(arr, len) { let p = 0 // 父级节点 while(len > 0) { p = (len - 1) >> 1 // (len & 1) 为0的情况下是有兄弟节点的,选出最大的与父级节点比较 if ((len & 1) === 0 && arr[len] < arr[len - 1]) len-- if (arr[len] <= arr[p]) break [arr[len], arr[p]] = [arr[p], arr[len]] len = p } }
在有序堆中每次添加和删除元素后执行的下沉和上浮操作,都会得到目前有序堆中的最大(小)元素,以此特性就可以进行对元素排序。
function heapSort(arr) { let len = arr.length let copy = [] // 建立一个有序的堆 for (let i = (len - 1) >> 1; i >= 0; i--) { sink(arr, i, len) } // 每次将堆顶元素与堆尾元素进行替换,再进行堆顶元素的下沉且堆长度减一,以此可以得到一个有序的数据 while(len--) { [arr[0], arr[len]] = [arr[len], arr[0]] sink(arr, 0, len) } }
大顶堆的的排序得到的是一个降序排序,小顶堆的则得到的是升序数据。
简单描述各排序算法的性能特点:
| 算法 | 是否稳定 | 是否原地排序 | 时间复杂度 | 空间复杂度 | 备注 |
| 选择排序 | 否 | 是 | N2 | 1 | 取决于输入元素的排列情况 |
| 插入排序 | 是 | 是 | 介于N和N2之间 | 1 | |
| 希尔排序 | 否 | 是 | NlogN? N6/5? |
1 | |
| 快速排序 | 否 | 是 | NlogN | lgN | 运行效率由概率提供保证 |
| 三向快速排序 | 否 | 是 | 介于N和NlogN之间 | lgN | 运行效率由概率保证,同时也 取决于输入元素的分布情况 |
| 归并排序 | 是 | 否 |
NlogN |
N | |
| 堆排序 | 否 | 是 | NlogN | 1 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号