十分强大的CC抛物线定理(数学)
鄙人自OI退役之后,潜心研究高考数学,在高二时偶然发现以下抛物线切线和焦点的奇妙关系,并窃称为CC抛物线定理。
然而如今疫情严峻,在家无聊便把这个有趣的东西拿出来跟各位分享一番。
OK,下面进入正题。
下面先看看是什么东西

为了能让我们在考试中合理运用,鄙人把适合在考试中写的证明过程写了一下

如果各位巨佬有什么更优秀更快的解法,欢迎提出。
OK,让我们看看这几个东西为什么会如此强大。
第一,这个垂直十分厉害。在解析几何大题之中,求面积的题目鄙人往往是用设点叉积暴力算,虽然也挺快的,但是却没有像垂直来的那么优美、便捷。
第二,你发现垂直对于求面积很有帮助,但是这些边却不好表示,这时,C抛三就能很好的解决这个问题。我们如果设∠OFD为θ,那么通过FO、θ和相似的配合,我们就可以十分轻松地表示出OD、FD、FB、BD的长度了,那么其它的一些运算也就变得轻而易举了。不管是什么面积还是长度都可以快速解决。
第三(这里用图表示)
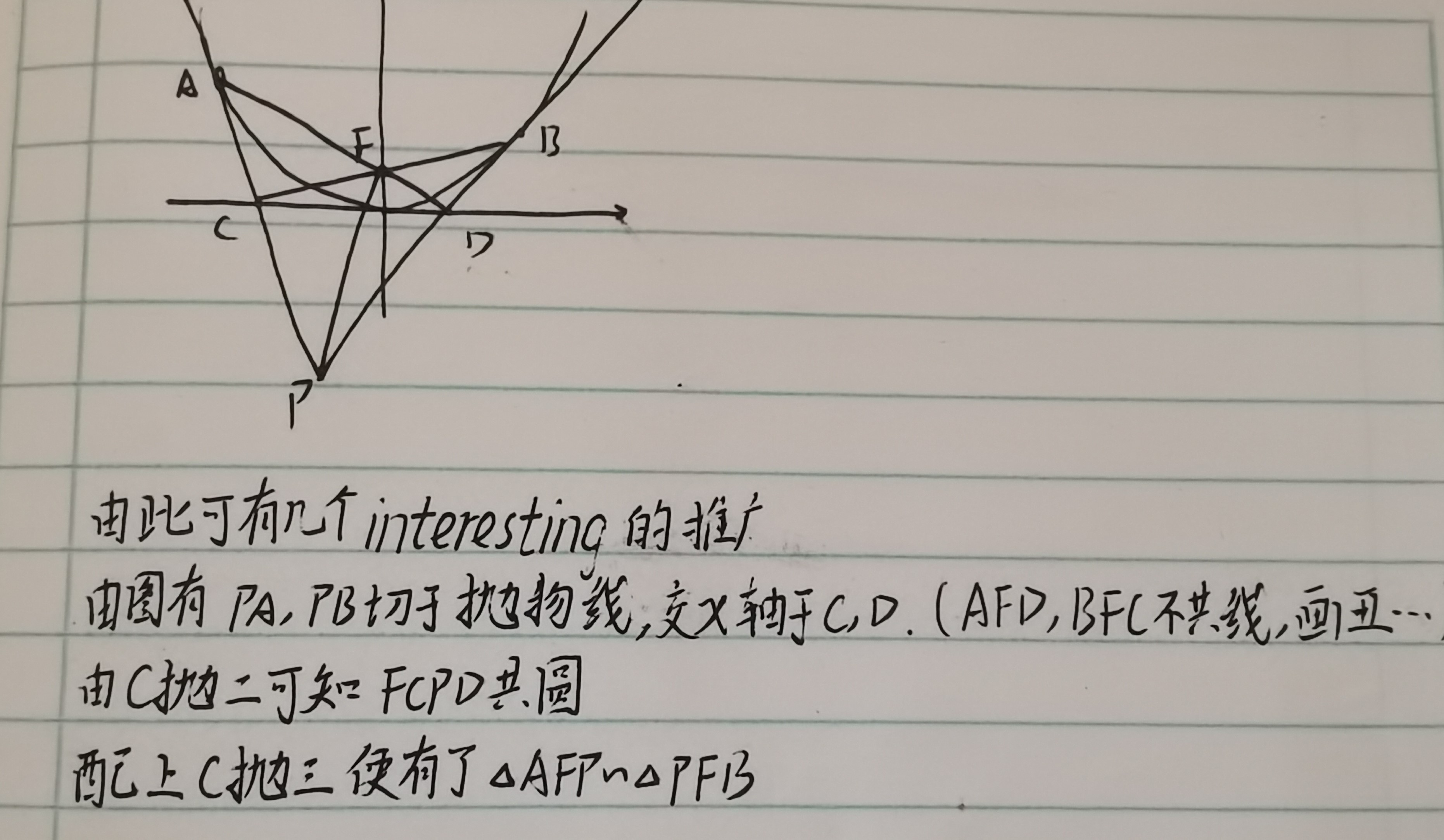
相信各位通过角转一下,相似一下很快就能得出上述结论,而许多题目所证明的往往是其中的一些特殊情况(比如AB过F点,则FP⊥AB,∠APB = 90° 等)。
尤记鄙人第一次用这个秒掉的题还是一道填海题,有些年代了,由于题目一下子没找到,说一下大概题意吧。
差不多是在一个过原点的单位圆和抛物线的公切线上乱搞长度比例关系,结果那个的标答写了两页A4,想想圆的切线,抛物线的切线,用CC抛物线定理简直不要太爽。。。
还有题目是限制P的移动,求PCD外接圆的直径范围,用定理也是秒杀了。。。
还有许许多多像这样抛物线切线和焦点搞来搞去的题目,但是万变不离其宗。鄙人所见抛物线切线与焦点产生一定关系的题目基本都可用CC抛物线定理大大简化运算或者直接秒杀,简直屡试不爽。
这或许就是发现数学本质的美好吧。(逃



