道路值守
题目描述
Z-Kingdom有着四通八达的现代化交通。时值独立庆典之际，随着来自周边国家旅客的日益增多，犯罪行为也悄无声息开始滋长起来。
特别任务支援科的警察们从总部收到了关于调查伪装在游客中的犯罪分子的请求。通过调查，他们得到了一张地图，记载了Z-Kingdom内每一条道路的长度。
显然，为了减少犯罪行为被发现的可能性，犯罪分子总是会选择最短的路径来行动。为了方便安排人手和推测犯罪分子采取的路线，他们希望得知任意两个地点之间，有多少条犯罪分子可能会选择的道路。
输入输出格式
输入格式：第一行，包含两个整数N，M，表示Z-Kingdom内的地点数和道路数。
接下来N行，每行包含三个整数x，y，z，表示道路连接的两个不同地点的标号，以及道路的长度。道路是双向的。
两个不同地点之间不会有超过一条道路。
输出格式：输出一行，包含 N (N-1)/2 个整数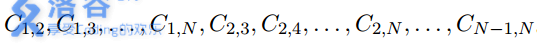
。
其中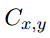
表示 x 号地点到 y 号地点之间有多少条犯罪分子可能会选择的道路。
输入输出样例
说明
【数据规模】
对于30%的数据，保证 N≤50
对于60%的数据，保证 N≤100
对于100%的数据，保证 N≤500。
【时空限制】
5s/128M
题解
先用Floyed求出各点之间的最短距离。
(下面用\(f_{x,y}\)表示\(x\)到\(y\)的最短距离，\(a_{x,y}\)表示连接\(x,y\)的边的长度)
枚举\(x\)，再枚举\(y,z\),若\(f_{x,y}+a_{y,z}=f_{x,z}\)，则说明\(x\)到\(z\)的最短路必定覆盖了\(a_{x,y}\)这一条边，所以\(++S[z]\)
\(S\)数组处理出来之后再枚举\(y,z\)\(f_{x,y}+f_{y,z}=f_{x,z}\)说明\(x\)到\(z\)的最短路经过\(y\)也就是存在\(s[y]\)条边，所以\(ans[x][y]=\sum{s[k]}\)
#include<bits/stdc++.h>
#define gc getchar
#define ll long long
inline ll read(){ll x = 0; char ch = gc(); bool positive = 1;for (; !isdigit(ch);
ch = gc()) if (ch == '-') positive = 0;for (; isdigit(ch); ch = gc()) x = x * 10
+ ch - '0';return positive ? x : -x;}inline void write(ll a){if(a>=10)write(a/10);
putchar('0'+a%10);}inline void writeln(ll a){if(a<0){a=-a; putchar('-');}write(a);
puts("");}
using namespace std;
const int N = 510, M = 500;
int n, m;
int f[N][N], s[N], ans[N][N], a[N][N];
int main() {
int x, y;
n = read(), m = read();
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; ++i) f[i][i] = 0;
for(int i = 1; i <= m; ++i) {
x = read(), y = read();
a[x][y] = a[y][x] = f[x][y] = f[y][x] = read();
}
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
for(int i = 1; i <= n; ++i) {
memset(s, 0, sizeof s);
for(int j = 1; j <= n; ++j)
if(i != j)
for(int k = 1; k <= n; ++k)
if(a[j][k])
if(f[i][j] == f[i][k] + a[k][j])
++s[j];
for(int j = 1; j <= n; ++j)
if(i != j)
for(int k = 1; k <= n; ++k)
if(f[i][j] == f[i][k] + f[k][j])
ans[i][j] += s[k];
}
for(int i = 1; i <= n; ++i)
for(int j = i + 1; j <= n; ++j)
printf("%d ", ans[i][j]);
return 0;
}
