前端程序员学好算法系列（八）二叉树和递归

257. 二叉树的所有路径
给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

输入:

1
/ \
2 3
\
5

输出: ["1->2->5", "1->3"]

解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3

解题：

1. root == null 直接return
2. 判断我们的路径是否到达到一个叶子节点中  if(root.left==null && root.right == null){ } 说明我们到达了一个节点 直接res.push(root.val) 然后返回当前值
3. 我们递归 调用binaryTreePaths(root.left) 返回左子树上满足条件的所有路径 ，遍历获得的路径 res.push(root.val+'->' lefts[i])  这样我们就获得了我们左子树上的所有路径；

4.同样方法获取右边的所有路径

 

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function(root) {
   let res = []
   if(root ==null){
       return []
   }
   if(root.left==null && root.right == null){
       res.push(String(root.val))
       return res;
   }
   let lefts = binaryTreePaths(root.left)
   for(let i=0;i<lefts.length;i++){
       res.push(String(root.val) + '->' +lefts[i])
   }
   let rights = binaryTreePaths(root.right)
   for(let i=0;i<rights.length;i++){
       res.push(String(root.val) + '->' +rights[i])
   }
   return res

};

437. 路径总和 III
给定一个二叉树，它的每个结点都存放着一个整数值。

找出路径和等于给定数值的路径总数。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

二叉树不超过1000个节点，且节点数值范围是 [-1000000,1000000] 的整数。

示例：

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1

返回 3。和等于 8 的路径有:

1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11

解题：

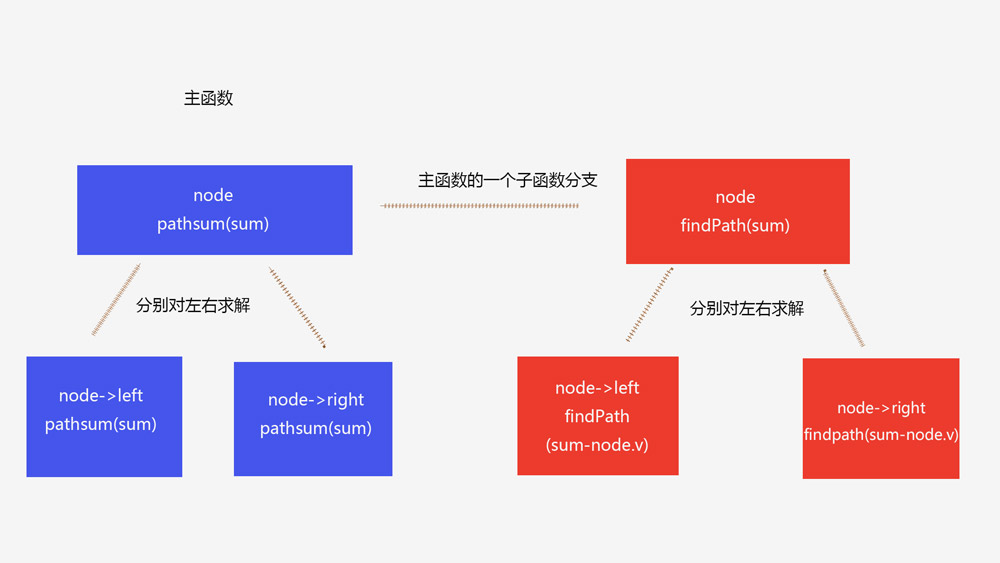
1.我们的主函数每次求解需要求解node node.left和node.right   求解node又需要求解其子函数findPath(sum) 和findPath(sum.left)和findPath(sum.right)
2.在findPath中由于node.val 存在负值所以我们不能直接求res = 1 需要 res+=1
3.我们用 findPath(root,sum); 求出从根节点出发所有可能的路径
4. 我们在分别从 pathSum(root.left,sum)  pathSum(root.right,sum)  从左右节点出发满足条件的路径

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {number}
 */
var pathSum = function(root, sum) {
      if(root == null)
        return 0
      let res = findPath(root,sum);
          res += pathSum(root.left,sum);
          res += pathSum(root.right,sum);
          return res
     // 在以node为根节点的二叉树中，寻找包含node的路径，和为sum
     // 返回这个路径的个数
     function findPath(node,num){
         if(node== null){
             return 0
         }
         let res = 0
         if(node.val ==num){
             res +=1;
         }
         res += findPath(node.left,num - node.val);
         res += findPath(node.right,num - node.val);
         return res
     }
};

 

235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

 

 

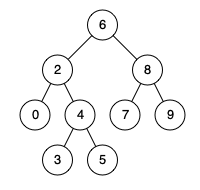
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

解题：
1.二叉搜索树满足，其任意左节点小于右节点，
2.当p和q分别在根节点的左边和右边时 根节点及为最近公共祖先
3.当 root.val>p.val && root.val>q.val  在root的左子树中寻找
4.当root.val<p.val && root.val<q.val 在root的右

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
      if(root==null){
           return root
      }
      if(root.val>p.val && root.val>q.val){
        return lowestCommonAncestor(root.left,p,q)
      }
      if(root.val<p.val && root.val<q.val){
        return lowestCommonAncestor(root.right,p,q)
      }
       
      return root

    
    
};

 

二叉树的js内容我们就先介绍到这里