前端程序员学好算法系列(七)二叉树和递归
144. 二叉树的前序遍历
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3] 1 \ 2 / 3 输出: [1,2,3]
有两种通用的遍历树的策略:
深度优先搜索(DFS)
在这个策略中,我们采用深度作为优先级,以便从跟开始一直到达某个确定的叶子,然后再返回根到达另一个分支。
深度优先搜索策略又可以根据根节点、左孩子和右孩子的相对顺序被细分为前序遍历,中序遍历和后序遍历。
宽度优先搜索(BFS)
我们按照高度顺序一层一层的访问整棵树,高层次的节点将会比低层次的节点先被访问到。
下图中的顶点按照访问的顺序编号,按照 1-2-3-4-5 的顺序来比较不同的策略。

解题:
1. 前序遍历口诀,递归终止条件 if(root==null) return
2. 前序遍历先打印root的值,递归遍历root的左子树, 递归调用root的又子树
3. 中序遍历 先递归遍历root的左子树,打印root的值, 递归调用root的又子树
4. 后序遍历 先递归遍历root的左子树, 在递归调用root的又子树, 打印root的值
5.前中后序遍历的不同之处在于打印root.val的时机,掌握一种,其他也很好掌握
/** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */ /** * @param {TreeNode} root * @return {number[]} */ var preorderTraversal = function(root) { let res = [] function pre(root){ if(root==null){ return } res.push(root.val) if(root.left){ pre(root.left) } if(root.right){ pre(root.right) } } pre(root) return res };
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回它的最大深度 3 。
解题:
我们知道,二叉树每个节点的深度与它左右子树的深度有关,且等于其左右子树最大深度值加上 1 。即:maxDepth(root) = max(maxDepth(root.left),maxDepth(root.right)) + 1
以 [3,4,20,null,null,15,7] 为例:
<1>我们要对根节点的最大深度求解,就要对其左右子树的深度进行求解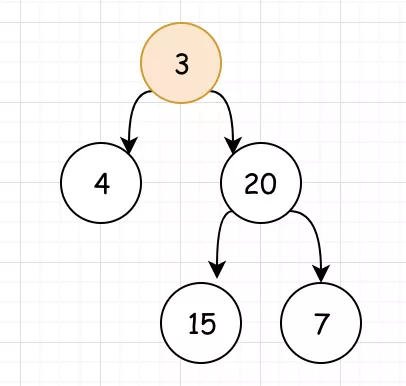
<2>我们看出。以4为根节点的子树没有左右节点,其深度为 1 。而以 20 为根节点的子树的深度,同样取决于它的左右子树深度。
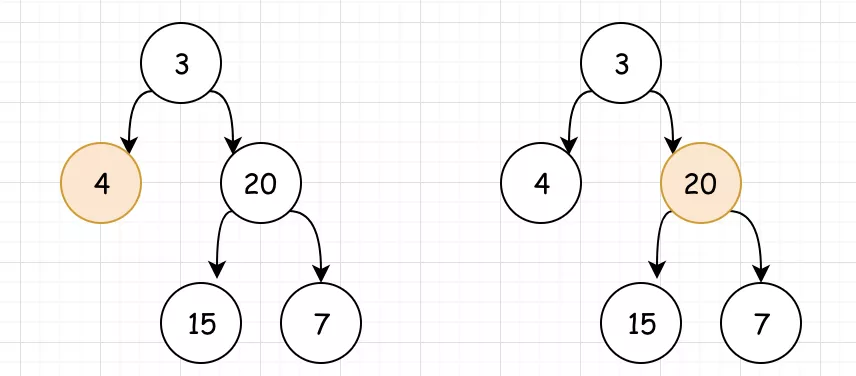
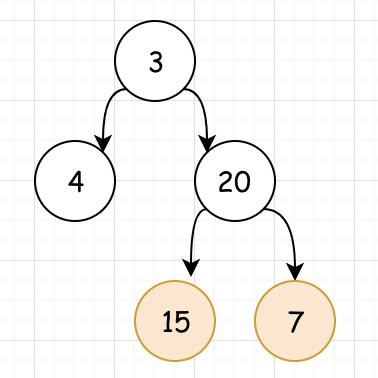
<3>对于15和7的子树,我们可以看出其深度为 2
/** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */ /** * @param {TreeNode} root * @return {number} */ var maxDepth = function(root) { if(root==null){ return 0 } return Math.max(maxDepth(root.left),maxDepth(root.right))+1 };
226. 翻转二叉树
翻转一棵二叉树。
示例:
输入: 4 / \ 2 7 / \ / \ 1 3 6 9 输出: 4 / \ 7 2 / \ / \ 9 6 3 1
解题:
1.js交换两个值A,B的重要事项 先缓存A let tmp = A ; 把A赋值B A = B; 把B赋值为缓存的tmp
2.我们这里也一样 递归终止条件 if(!root) return null
3.root存在时交换左右节点,在递归调用
/** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function(root) { if(!root) return null if(root) { var left = root.left root.left = root.right root.right = left } invertTree(root.left) invertTree(root.right) return root };
112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22, 5 / \ 4 8 / / \ 11 13 4 / \ \ 7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
解题:
1.求解从 root 到叶子节点是否存在路径和为 sum 的路径 hasPathSum(root, sum),可以转换成求解从 root.left 或者 root.right 到叶子节点是否存在路径和为 sum - root.val 的路径,即 hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val) 。
2.本题要求必须有叶子节点所有 当root只有一个元素且root.val ==sum时不是一个正确的解。
3.我们用 root.left==null && root.right==null 时判断最正确的解。
/** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */ /** * @param {TreeNode} root * @param {number} sum * @return {boolean} */ var hasPathSum = function(root, sum) { if(root==null){ return false } if(root.left==null && root.right==null){ return sum == root.val } if(hasPathSum(root.left,sum-Number(root.val))){ return true } if(hasPathSum(root.right,sum-Number(root.val))){ return true } return false };


 浙公网安备 33010602011771号
浙公网安备 33010602011771号