皮亚诺曲线距离

 

 

 

 

 

 

 

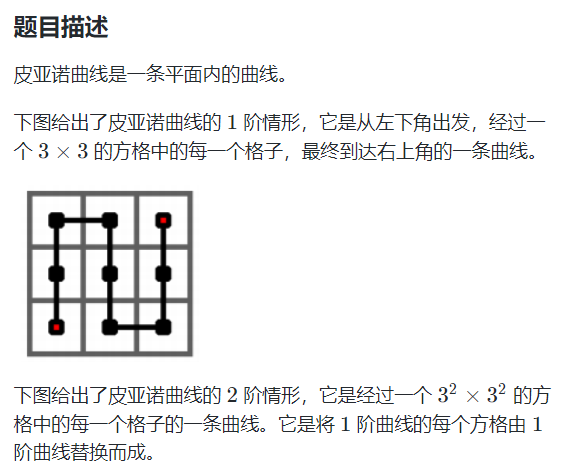
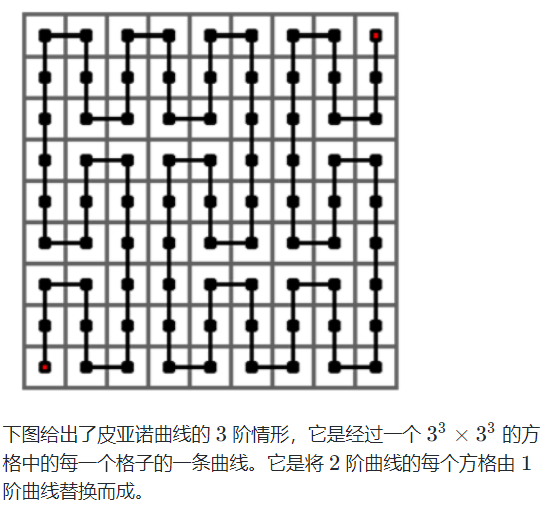
 思路：把每一个k阶看成一个3*3的网格，计算出点到每层（0，0）的距离，递归求出下一阶n-1的距离。

#include"stdio.h"
#include"math.h"
#include"string.h"
#include"iostream"
#include"algorithm"
using namespace std;
long long Pow(long long n,long long k)
{
    long long ans=1;
    while(k)
    {
        if(k%2==1)
        {
            k--;
            ans=ans*n;
        }
        k=k/2;
        n=n*n;
    }
    return ans;
}
long long dfs(long long k,long long x,long long y)
{
    if(k==0)return 1;
    if(k>=40)k=39;
    long long m=Pow(3,k-1),a=x/m,b=y/m,xx=x%m,yy=y%m,ans=0;
    if(a==0&&b==0)return dfs(k-1,xx,yy);
    else if(a==0&&b==1)return 1*m*m+dfs(k-1,m-xx-1,yy);//关于过中心且竖直向下的直线对称  
    else if(a==0&&b==2)return 2*m*m+dfs(k-1,xx,yy);
    else if(a==1&&b==2)return 3*m*m+dfs(k-1,xx,m-yy-1);//关于过中心且水平向左的直线对称  
    else if(a==1&&b==1)return 4*m*m+dfs(k-1,m-xx-1,m-yy-1);//关于中心对称  
    else if(a==1&&b==0)return 5*m*m+dfs(k-1,xx,m-yy-1);//关于过中心且水平向左的直线对称  
    else if(a==2&&b==0)return 6*m*m+dfs(k-1,xx,yy);
    else if(a==2&&b==1)return 7*m*m+dfs(k-1,m-xx-1,yy);//关于过中心且竖直向下的直线对称  
    else if(a==2&&b==2)return 8*m*m+dfs(k-1,xx,yy);
}
int main()
{
    long long k,x1,x2,y1,y2;
    cin>>k>>x1>>y1>>x2>>y2;
    long long ans=dfs(k,x2,y2)-dfs(k,x1,y1);
    if(ans<0)ans=-ans;
    cout<<ans;
}