N 皇后
题目:
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
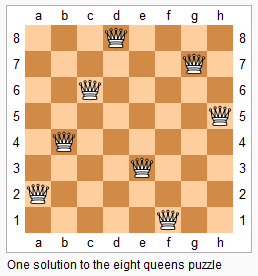
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
解题思路:用回溯解决,先初始化一个数组作为棋盘,再对每一行进行判断
class Solution {
private List<List<String>> ans = new ArrayList();
public List<List<String>> solveNQueens(int n) {
char[][] board = new char[n][n];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
board[i][j] = '.';
}
}
dfs(board, 0);
return ans;
}
private void dfs(char[][] board, int row) {
if(row == board.length) {
ans.add(construct(board));
return ;
}
for(int i = 0; i < board.length; i++) {
//判断当前位置是否可以放皇后
if(check(board, row, i)) {
board[row][i] = 'Q';
dfs(board, row + 1);
//将放下的皇后拿起来
board[row][i] = '.';
}
}
}
private boolean check(char[][] board, int row, int col) {
//行
for(int i = row - 1; i >= 0; i--) {
if(board[i][col] == 'Q')
return false;
}
//列
for(int i = col - 1; i >= 0; i--) {
if(board[row][i] == 'Q')
return false;
}
//左上角
for(int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if(board[i][j] == 'Q')
return false;
}
//右上角
for(int i = row - 1, j = col + 1; i >= 0 && j < board.length; i--, j++) {
if(board[i][j] == 'Q')
return false;
}
return true;
}
//将数组转化成list
private List<String> construct(char[][] board) {
List<String> list = new ArrayList();
for(int i = 0; i < board.length; i++) {
list.add(new String(board[i]));
}
return list;
}
}





