892.surface area of 3D shapes
892. Surface Area of 3D Shapes
N * N grid, we place some 1 * 1 * 1 cubes.Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).
Return the total surface area of the resulting shapes.
Example 1:
Input: [[2]]
Output: 10
Example 2:
Input: [[1,2],[3,4]]
Output: 34
Example 3:
Input: [[1,0],[0,2]]
Output: 16
Example 4:
Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 32
Example 5:
Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 46
如果理解该题意思后，那么该题常常活跃于小学生的数学练习册。
这个题目我认为有两个难点，一是理解v = grid[i][j] ，这玩意到底和example里面的数组啥关系？
一开始也是蒙圈，后来明白了。其实就是二维数组里面，某个元素从外到内的索引值i，j分别代表其在N*N个格点里面的坐标。
v值代表高度。例如，
[[2]] 仅有一个元素其索引为[0][0] 那么它坐标就是(0,0) 高度为2，即(0,0)==2.由于有两面重合，那么面积为10；
[[1,2],[3,4]]有四个元素，对应四个坐标，(0,0)==1 (0,1)==2 (1,0)==3 (1,1)==4.面积待会儿再说，这里把这个坐标讲明白。
外层元素的个数为x方向坐标，内层元素个数为y方向坐标，元素值为z坐标。
另一个难点就是计算表面积的算法了，小学生靠数，你哎？
数是不可能数的。我的思路是作减法，把所有小方块的面积先求出来，再减去会有重合的。
哪些会有重合？x、y、z三个方向都会有重合，
假设不悬空的话，图里是7个方块，x方向有1个重合，y方向有3个重合，z方向有3个重合。
所以表面积就是7*6 - 2*(1+3+3) =28.
怎么我们发现第一部分表达为程序只是遍历求和即可，但是各个方向的重合数怎么求？
还是这幅图，我们得到的其实是俯视图，即z被压缩成一个值了，我门看到的是x、y和z的值。
z方向的重合数就是每个xy坐标对应值-1。how about xy？
有点类似水桶一样，决定水位的是最低那块木头的高度，这个也是。
我们观察到两两坐标对应值较小的即为一个重合，xy方向都是如此。所以我们只需要在前面遍历时，在合适的地方统计这些重合数，最后减去重合的面即可。
为了满足题意，其实是满足oj测试的规则，也简化我们的程序，上图应该化为
这样程序内层遍历的阈值才相同。值得一提的是补0占位置后，z要加判断。
这个图对应的输入应该为
[[3,2,1],[1,0,0]]
点开c++不熟悉二维vector，就用c实现了
1 #define min(x,y) ((x)<(y))?(x):(y) 2 3 int surfaceArea(int** grid, int gridSize, int* gridColSize){ 4 int quantityOfGrid=0; 5 int overlapOfZ=0; 6 int overlapOfX=0; 7 int overlapOfY=0; 8 for (int i=0;i<gridSize;i++){ 9 for (int j=0;j<*gridColSize;j++){//grid[i][j] 10 int quantityOfAordination=grid[i][j]; 11 quantityOfGrid += quantityOfAordination; 12 if (quantityOfAordination) //!=0 13 overlapOfZ += quantityOfAordination-1; 14 if (i>0) 15 overlapOfX += min(grid[i-1][j],grid[i][j]); 16 if (j>0) 17 overlapOfY += min(grid[i][j-1],grid[i][j]); 18 } 19 } 20 return (quantityOfGrid*6) - 2*(overlapOfY + overlapOfX +overlapOfZ); 21 }
我们输入
[[3,2,1],[1,0,0]]
尴尬的是，
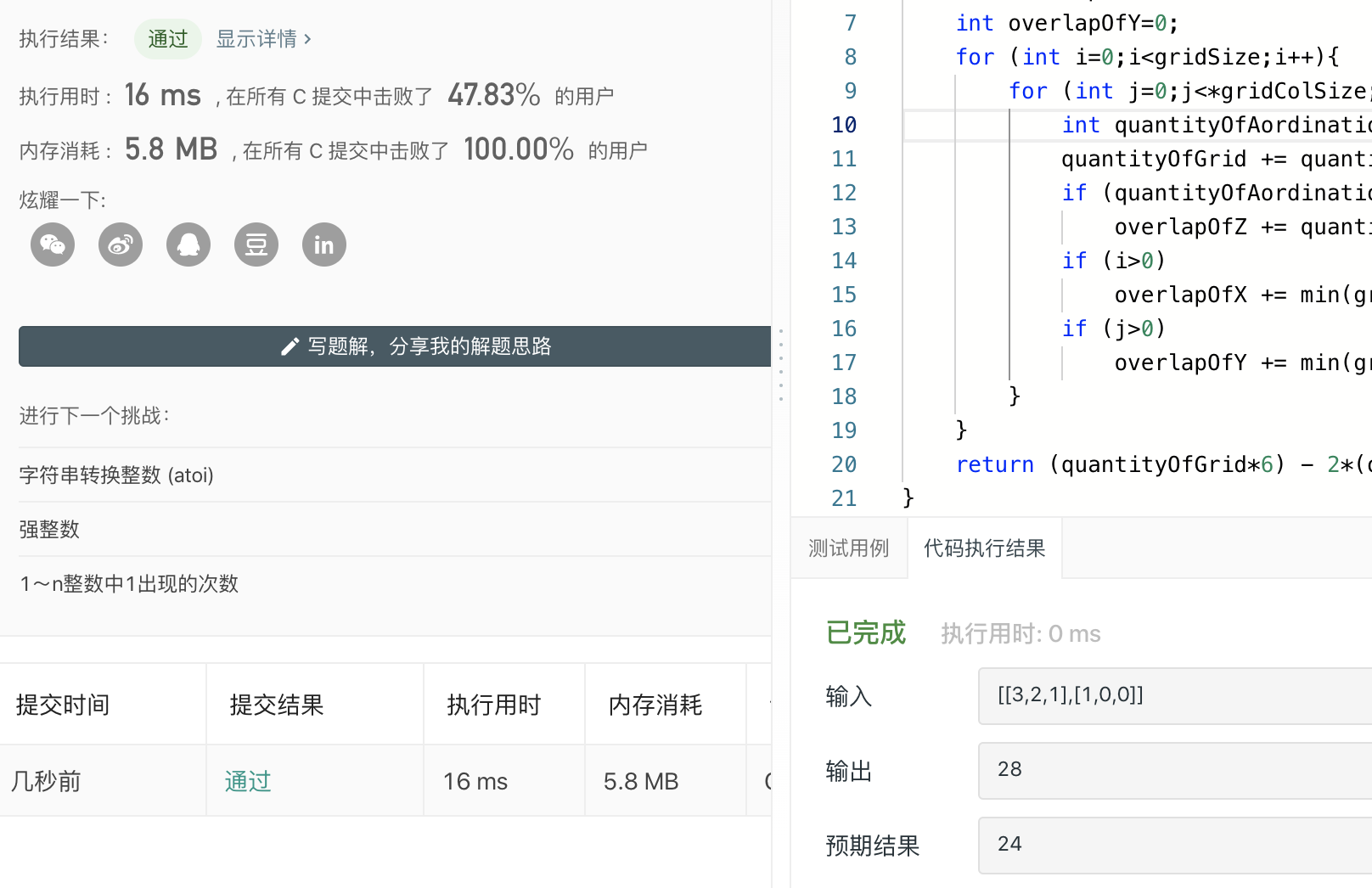
我们通过了，我的输出也是手工算的结果。但是似乎和它的输出不同？？？
