递归之617.merge-two-binary-trees & 226.invert-binary-tree
1 Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. 2 3 You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree. 4 5 Example 1: 6 7 Input: 8 Tree 1 Tree 2 9 1 2 10 / \ / \ 11 3 2 1 3 12 / \ \ 13 5 4 7 14 Output: 15 Merged tree: 16 3 17 / \ 18 4 5 19 / \ \ 20 5 4 7 21 22 23 Note: The merging process must start from the root nodes of both trees. 24 25 来源:力扣(LeetCode) 26 链接:https://leetcode-cn.com/problems/merge-two-binary-trees 27 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这段见解我有新体会会更新
看到题目第一时间考虑使用层序遍历,想绕开递归。对于设计递归算法有种莫名的排斥,虽然总是看到“递归简化程序”,程序是简化了,但是设计程序并未简化。
下为本人对递归粗浅理解。
设计一个递归函数要有三个要点:
1.递归什么时候退出?
这个情况一般是一个具体问题最“简单”的情形,拿二叉树来说,一般就是当前指针为空指针。
2.一次递归调用需要做什么?
3.当前调用给上一级调用返回什么?
2和3通常需要一起考虑。递归要退出不陷入栈溢出,那么一定有返回,可以没有返回值。
递归的返回值可以由问题确定,比如求二叉树深度,返回的一般就是深度,这个返回是每次都用得上的。
有时候考虑问题不清楚,会陷入返回两个或多个参数的情形,
这个时候可以尝试把问题分解,添加子函数实现一部分逻辑,如判二叉树平衡,写子函数来求节点深度,目标函数层序遍历判断平衡否;
或者添加一个全局变量或者外部变量的引用,如BST🌲,变大🌲(每个节点值变为其与比他大的值的和),在交换L、R节点的中序遍历时不断累计和到全局变量。
或者设计一个返回值结构体,拿来作返回,如判平衡二叉树,返回一个具有两个成员的结构体,一个是当前平衡否,另一个是树的深度。
有时候问题要求的结果不是数值,而是要求实现某一过程,这个时候就可以没有返回值,比如我这道题的一个实现(我添加的子函数实现特定功能)。
但是该类题目往往要求最终返回根结点的指针,所以可以把这个子函数去掉(下面也做了这个操作),直接在目标函数最后加上一个返回根结点指针。此时只有最先压入栈的节点,
也就是最后弹出的节点返回时有用(返回root给OJ)。
然而有时候把这两个思路搞到一起,特别是二叉树,当决定采用某种顺序遍历时,会陷入不是只有root==null这里才能返回吗?的🤔。而想不到在最后加上一句return root;
其实这个时候大可把实现主要功能的这个部分写成子函数,目标函数调用它,并返回root即可,这样思路更加清晰。但是熟悉之后也无所谓了,只是多一个考虑而已。
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 12 public: 13 void recursive(TreeNode* &t1, TreeNode* t2){ 14 if (t1==nullptr || t2==nullptr){ 15 if (t2) 16 t1=t2; 17 return; 18 } 19 t1->val+=t2->val; 20 21 recursive(t1->left,t2->left); 22 recursive(t1->right,t2->right); 23 } 24 TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) { 25 recursive(t1,t2); 26 return t1; 27 } 28 };
在这个实现里,没有新建树,把树1作为最终的树,在它身上修改。设计了一个子函数来实现merge,这个函数就没有返回值,它只是遍历两棵树。
最后只需要返回t1指针即可。值得注意的是,在recursive的工作栈里,获取了t1的引用(t2则不需要),这是因为第16行,t1=t2;改变的是指针的值,而非指针指向的值。
去掉子函数recursive后,等价程序
1 class Solution { 2 3 public: 4 TreeNode* mergeTrees(TreeNode* &t1, TreeNode* t2) { 5 if (t1==nullptr || t2==nullptr){ 6 if (t2) 7 t1=t2; 8 return t1;//case-> 1:[] 2:[1] 9 } //1 10 t1->val+=t2->val; //2 11 12 mergeTrees(t1->left,t2->left); //3 13 mergeTrees(t1->right,t2->right); //4 14 15 return t1; //5 16 } 17 };
在当前层,即访问t1,t2时,直接修改t1的值(注意!不是修改t1指向的内容的值。这也是为什么要改形参为引用)
以下使用测试例子逐步展示递归执行过程(这个方法参考b站李卓老师的二叉树视频)
我们把整个方法分为5个代码段(见双斜线)
L(x), R(y)分别代表左右树的节点,其中x、y为节点值。方格为当前迭代执行的代码块。
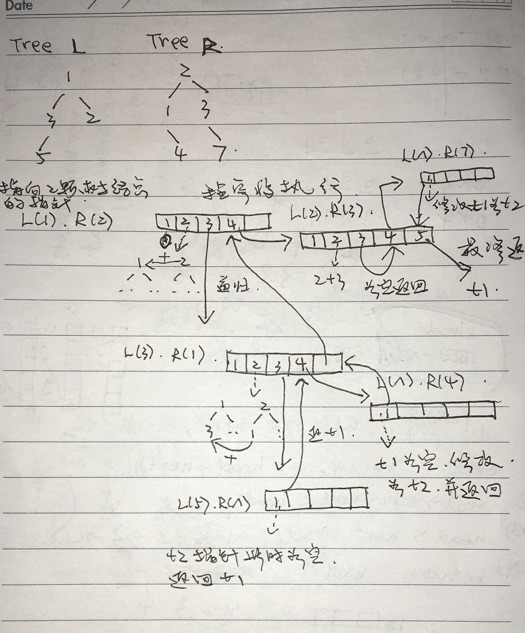
挑选L(1) R(2) 迭代作简要解释。在当前迭代,L(1)即左树的根结点,R(2)为右树根结点。
代码段1不满足条件,直接退出。
代码段2将左树的1加上右树的2.
代码段3进入第一次递归,分别传入左树右树的左子树。传入的子树为左树的3,右树的1。然后进入子树的迭代。
整个流程从左到右跟随箭头方向执行,最终返回被修改的t1树。该树即为所求。
大致瞟了一眼别人的思路,参数不再需要引用,其实就是利用当前迭代的两个递归返回。两个返回即为当前节点的左右子树,加一个赋值操作即可。
1 class Solution { 2 public: 3 TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) { 4 if (t1==nullptr || t2==nullptr) 5 return (t2)?t2:t1; 6 t1->val+=t2->val; 7 TreeNode *p=mergeTrees(t1->left,t2->left); 8 TreeNode *q=mergeTrees(t1->right,t2->right); 9 t1->left=p;t1->right=q; 10 return t1; 11 } 12 };
同步后序(为什么是后序?第6行不是先操作的根节点?注意:这里把第9行看作对根节点的操作,其实什么序遍历无所谓,实际上这里是 根左右根 的遍历顺序)遍历两棵树,当前节点返回的入口有两个,第5行有空节点,第10行当前节点操作完返回。返回给上一级节点的值,均为指向当前迭代的指向左树的指针。这个实现里,t1树的左右子树均被重新更新!
还是以上图来作解释,我们选取 L(5) R(^) 节点,此时返回指向L(5)的指针给L(3) R(1)节点被赋值为p;L(^) R(4)节点,返回指向R(4)的指针给L(3) R(1)节点被赋值为q。此时L(3) R(1)节点有4个相关节点指针,分别为指向L(3)、R(1)、应为的L(3)的左右子树的指针。这个时候只需要把L(3)的左右子树更新以下,即更新L(3)的左右指针域分别为p、q指针即可!
值得一提的是,我翻看了内存占用量小的实现。同类递归实现中,他们减少了栈的深度,在合适的地方让某些返回直接返回nullptr可减少一层递归。
3-27 update:
上面程序可以更改为如下程序:
1 class Solution { 2 public: 3 TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) { 4 if (t1==nullptr || t2==nullptr) 5 return (t2)?t2:t1; 6 t1->val+=t2->val; 7 t1->left=mergeTrees(t1->left,t2->left); 8 t1->right=mergeTrees(t1->right,t2->right); 9 //t1->left=p;t1->right=q; 10 return t1; 11 } 12 };
即去掉两个local varirable,实际从执行结果上看没什么区别。但是我们编写程序的逻辑执行过程是不同的。
前者使用临时变量p,q;后者直接对left,right赋值,不同的就是赋值位置。

我们考虑L(3),R(1)两个节点,
此时按前者执行:
L(5)入栈,R(^)入栈,返回L(5)存于p;
L(^)入栈,R(4)入栈,返回R(4)存于q;
然后令L(3)的左右指针即left、right分别为p,q。
若按后者执行:
L(5)入栈,R(^)入栈,返回L(5)赋值给L(3).left;
L(^)入栈,R(4)入栈,返回R(4)赋值给L(3).right;
因此只是两颗子树更新的时刻不同而已。
但是下面的题目,就有不同了。
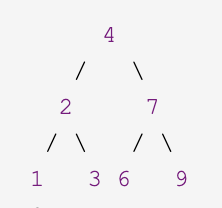
Invert a binary tree. Example: Input: 4 / \ 2 7 / \ / \ 1 3 6 9 Output: 4 / \ 7 2 / \ / \ 9 6 3 1
程序:
1 class Solution { 2 public: 3 TreeNode* invertTree(TreeNode* root) { 4 if (root==nullptr) 5 return root; 6 TreeNode *l=invertTree(root->left); 7 TreeNode *r=invertTree(root->right); 8 root->left=r; 9 root->right=l; 10 return root; 11 } 12 };
我们这里假设有一份程序是把该程序6-9行合并为诸如root->right=invertTree(root->left), root->left=invertTree(root->right)
并仍成为前者,把未合并的称为后者。
考虑root(2)节点,若执行前者程序:
L(1)入栈,
空指针入栈退栈返回空指针,L(1)的right赋值为空,同理left也被赋值为空。(都是空看不出什么,我们把1的右指针省略)
L(1)退栈,
把L(1)的指针赋值给L(2)的right (即指向值为1的节点的指针赋值给值为2的节点的right指针域,等价于此时2的两颗子树都成了1)
由于2的两个子树都是1,交换已经失败了。
若执行后者程序:
L(1)入栈,
空指针入栈退栈返回空指针,L(1)的right赋值为空,同理left也被赋值为空。(都是空看不出什么)
L(1)退栈,把L(1)的指针赋值给本地变量l。
同理执行如上几步,把R(3)的指针赋值给本地变量r。
此时再直接统一赋值root(2)节点的左右指针域。交换成功!
之所以特地写这个是为了明白,我们在对递归不熟悉的时候,往往会沿用以前使用过的思路,
但是具体问题要具体分析,它们可能确实相似,但是是否能满足当前的需求,还是要按照递归算法编写思路走!
ref:http://39.96.217.32/blog/4#comment-container

 浙公网安备 33010602011771号
浙公网安备 33010602011771号