BUAA_OO_2021_第一单元总结
BUAA_OO_2021_第一单元总结
第一单元的作业是对表达式进行求导,从第一次作业的简单幂函数,到第三次的三角函数和嵌套规则,难度逐渐递增。但都应当分解成五个子步骤分别进行编程:解析表达式、存入数据结构、递归求导、化简、递归打印。如果这第一步的分解都没有做好,比如有些同学写出了“面向字符串求导”、“面向字符串化简”的代码,就会使代码逻辑耦合过强,不易debug,而且很容易出现情况考虑不周到导致bug一片。
第一次作业
作业思路
数据结构
第一次作业是针对幂函数进行求导,写程序要先从数据结构下手,任何幂函数都具有一般形式
,因此可以用一个List<幂函数单项式>来表示一个幂函数多项式,幂函数单项式则表示为Tuple<系数, 指数>的二元组。据此我确认了我的类结构:

为了优化化简合并同类项的效率,多项式中采用了TreeMap<指数, 多项式>的容器。
表达式解析
然后考虑解析表达式的方法。解析工作表面上是编程,实际上更像是在做数学证明,如何保证针对每一个合法的字符串都能正确解析为结构化数据需要大量理性的思考,找出一条简洁且保证正确的路。我的思路是先根据加减号将多项式分割成单项式,再根据乘号将单项式分割成因子,为此我找到了两个简洁的用于分割字符串的正则表达式(另外:考虑到空白字符完全没有用就在预处理时删掉了)
[x\d](?=[+-]) 紧跟在数字或x后面的加减号一定用于分割单项式
(?<!\*)\*(?!\*) 单个*而不是两个连续的**一定是用于分割因子的乘号
这样我就完成了解析工作,后续的求导和输出步骤都不难,关键在化简。
优化方法
化简的方法不外乎以下3种:
- 已经化为一般形式
- 尽可能令第一项为系数为正,省去首项的正号
x**2输出为x*x的形式可以省去一个字符
可以证明这就是最优的化简思路
代码结构分析
| Class | Cons | CSA | CSO | CSOA | LCOM | OCavg | OCmax | OSavg | WMC |
|---|---|---|---|---|---|---|---|---|---|
| MainClass | 0 | 0 | 13 | 13 | 1 | 3.00 | 3 | 10.00 | 3 |
| Monomial | 2 | 2 | 27 | 29 | 1 | 1.87 | 7 | 3.47 | 28 |
| Polynomial | 1 | 1 | 17 | 18 | 1 | 4.60 | 10 | 11.80 | 23 |
| Total | 3.0 | 3.0 | 57.0 | 60.0 | 54.0 | ||||
| Average | 1.0 | 1.0 | 19.0 | 20.0 | 2.57 | 6.67 | 5.76 | 18.0 | 1.0 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Monomial.toStringNoSign() | 13 | 7 | 4 | 7 |
| Polynomial.parse(String) | 10 | 3 | 4 | 9 |
| Monomial.parse(String) | 9 | 1 | 4 | 6 |
| Polynomial.addMonomial(Monomial) | 7 | 2 | 4 | 5 |
| Polynomial.toString() | 6 | 4 | 4 | 5 |
| … | … | … | … | … |
| Total | 54 | 36 | 41 | 54 |
| Average | 2.57 | 1.71 | 1.95 | 2.57 |
根据数据可以看出代码复杂度和类的耦合度都比较低,其中Monomial.toStringNoSign()涉及到了较为复杂的化简输出逻辑,需要针对单项式系数和指数进行二维的分类讨论,并不能进行进一步的降低复杂度。
测试方法
我利用python实现了全自动出题+判答案的测评机,进行大量的随机测试和部分手搓极限数据测试
出题机构造方法
关于出题机,我的目标是:凡是合法的数据,均存在被生成的可能性。如果符合了这条目标,只需要测试时间足够长,测试的覆盖率就会逐渐接近100%。
而为实现上述目标,只需要翻译题目中提供的形式化表达,表达式中的可选项以一定的概率出现,以一定的概率不出现。
在尝试使用xeger生成数据时,发现项和表达式的自调用式定义并不能直接翻译成正则表达式,虽然勉强可以通过转换写出一个来,但是这并不是长久之计。
于是我直接用python进行编程,来实现递归和随机,事实证明这个做法是具有前瞻性的。在后面的作业中xeger的方法会完全失效或无法生成足够强力的数据,而我的这个方法只需要稍加补充就可以实现生成新的数据。
另外不得不提到的是对同质测试数据的理解,举例来说对于数字,如果输入中出现5没有问题,那么把5换成6也显然不会有问题,这就说明5和6是同质的,在生成测试数据是不应该让大量同质数据出现。于是可以使用常数池这样的概念,如果需要生成一个常数,仅需从常数池里任意选取一个数就代表了所有的自然数,常数池应该包括以下数字:
- 边界值:如0、1、2、3
- 一般值
(恶臭值):如114514、1145141919810 - 超大值(应大于\(2^{64}\)):如31415926535897932384626
- 格式奇异值:如00、00800、0008008000、0000114514
答案自动评判
感谢sympy的存在,判答案是无比简单的一件事,只需要预处理掉前导0、使用sympify转换然后调用equals方法就可以很快的判断正误。
关于测评
本次作业没有在中测、强测和互测中出现bug。
在互测时,鉴于手上有着不错的评测机,我将同房间同学的代码直接打包成jar放入评测机进行批量黑盒测试,很快就发现了组内存在的所有bug,效率极高。
互测共发现了三个bug
- 第一个同学会将
-1*x**-2输出为x**2,具体一看,原来是使用了一个将符号和绝对值分别保存,判断时把绝对值当数用了,这也难怪,他管常数类中绝对值的命名叫做num,管系数叫base,管指数叫index,命名望文失意,亟待改正。 - 第二位同学会错误识别-+-为负号,他的正则表达式十分复杂,完全看不懂逻辑,这可能是他考虑不全的原因。
- 第三位同学会对
+x**+a+x**+b产生问题,也可能是因为正则表达式很复杂没有考虑全。
第二次作业
作业思路
数据结构
第二次作业中出现了三角函数因子和表达式因子,意味着表达式允许进行多级嵌套,数据结构需要进行比较大的改变,表达式的解析工作也因为括号的出现不能延续第一次作业的方式。于是我直接进行了全面的重构。
主要的类包括表达式类Expression(用加法连接存储的各个项),项类Term(用乘法连接储存的各个因子)以及因子抽象类Factor(代表因子)。所有的类均实现了Derivable接口,实现了derivative()方法返回对象自身数学意义的导数。
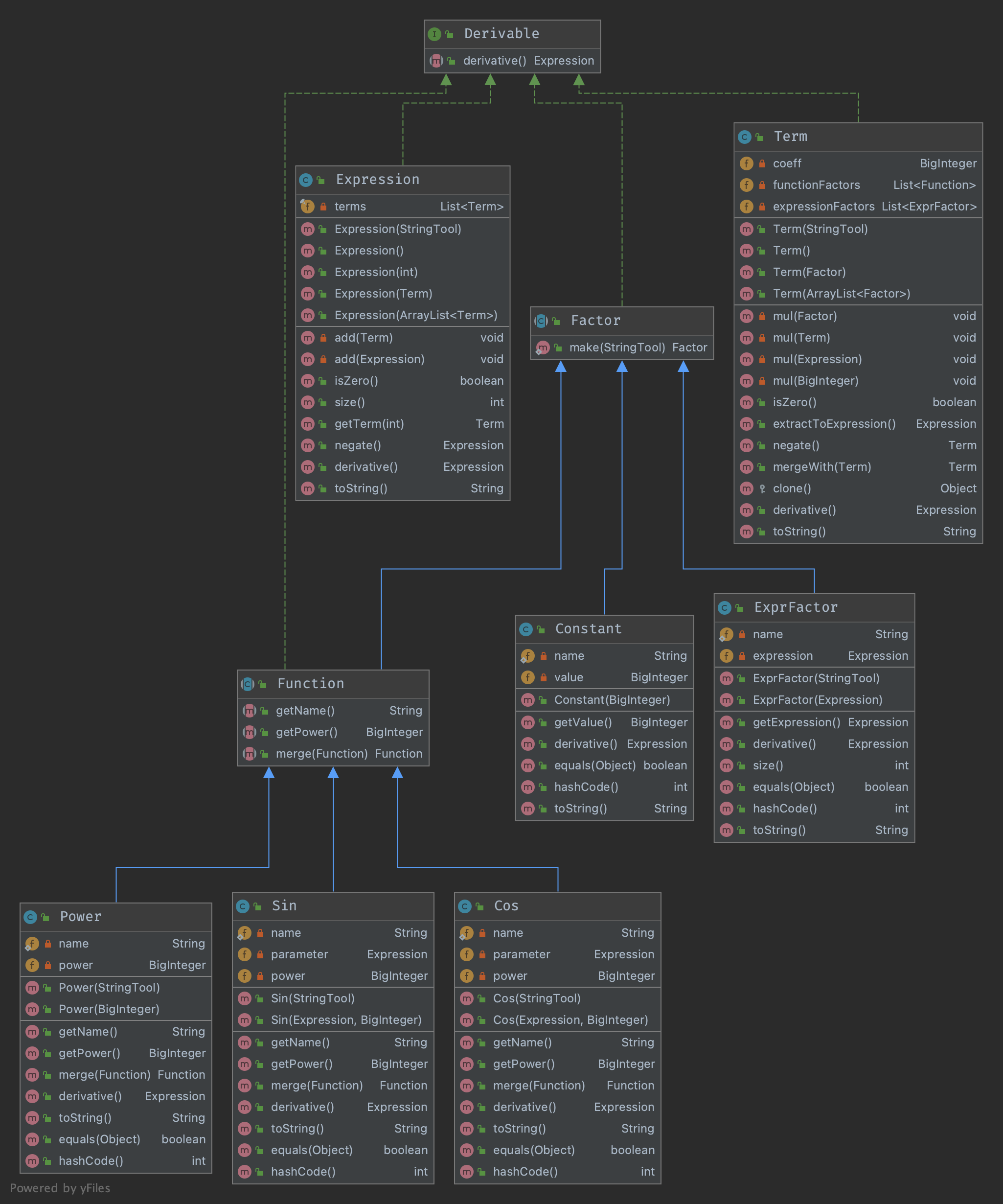
表达式解析
因为这次作业出现了括号,没法找到一个简洁的方式直接将表达式分割成项,如果非要这么做的话,则需要维护一个括号匹配栈,写起来十分复杂,将项分割成因子时也同样需要使用括号匹配栈,让代码的复杂量翻倍。同时,这样的解析方法将会具有\(O(N^2)\)的时间复杂度,可能会被卡TLE。
于是我决定尝试大佬们在第一次作业时常常提起的递归下降。我参考了网上的教程理解的递归下降的思想,而在实现的时候,我不想在每个类中都写复杂的字符串扫描方法,于是我实现了一个工具类StringTool,只需要在构造这个工具的时候喂给它一个字符串,就可以问它能否扫描到符合条件的字符,如果有则自动将其消耗。(实际上,我曾尝试使用Scanner, Pattern这两个类,但是都不能满足我的需求,于是才选择了自己创造)
于是,我的每一个类都存在一个参数为StringTool的构造方法,从其中读取自身所需要的字符并返回该类的对象,抽象类Factor则有一个工厂方法make()来制造一个因子 。
递归下降既可以将时间复杂度优化到\(O(N)\),又可以非常简单清晰的表达逻辑,还有就是递归下降针对第三次作业对于错误格式的判断是水到渠成的。
优化思路
首先我认为将所有括号全部展开是不利的,第一是时间复杂度和空间复杂度都很高,第二是写起来麻烦,所以我选择只拆那些拆了不会有影响的括号,然后带着括号直接进行求导。至于三角函数化简,我认为这并不重要,所以就没有去做。以下是我做了的优化:
除了最后两行的化简是在输出的时候考虑的,其余的化简都在读入的时候顺便实现,读到这里,你可能会认为读入和化简一起进行会导致耦合性变高,但其实不是这样的。我为函数的构造方法提供了很多辅助函数,比如Expression类中的private add方法和Term类中的private mul方法,这些方法使用多种不同类型变量进行重载,方法的含义是使得当前类的数学意义加上(add)和乘上(mul)参数的数学意义。这些辅助函数会尝试解包,如果解包成功则会调用其他辅助函数,如果解包不成功才直接放到列表里,最终递归实现构造。这样的实现使得方法意义十分明确,代码结构不复杂,而化简的逻辑可以方便的同时应用于解析和求导,使得时间复杂度也大大降低(相对于解析后不化简直接求导)。
代码结构分析
| Class | Cons | CSA | CSO | CSOA | LCOM | OCavg | OCmax | OSavg | WMC |
|---|---|---|---|---|---|---|---|---|---|
| main.Expression | 5 | 1 | 26 | 27 | 1 | 2.31 | 6 | 4.38 | 30 |
| main.Factor | 0 | 0 | 14 | 14 | 1 | 5.00 | 5 | 10.00 | 5 |
| main.MainClass | 0 | 0 | 13 | 13 | 1 | 3.00 | 3 | 12.00 | 3 |
| main.Term | 4 | 3 | 28 | 31 | 1 | 3.73 | 13 | 9.87 | 56 |
| main.factor.Constant | 1 | 2 | 19 | 21 | 2 | 1.33 | 3 | 1.83 | 8 |
| main.factor.ExprFactor | 2 | 2 | 21 | 23 | 1 | 1.25 | 3 | 1.75 | 10 |
| main.factor.Function | 0 | 0 | 16 | 16 | 3 | n/a | n/a | n/a | 0 |
| main.function.Cos | 2 | 3 | 25 | 28 | 2 | 1.78 | 3 | 4.44 | 16 |
| main.function.Power | 2 | 2 | 25 | 27 | 2 | 1.78 | 3 | 3.44 | 16 |
| main.function.Sin | 2 | 3 | 25 | 28 | 2 | 1.78 | 3 | 4.22 | 16 |
| main.tool.StringTool | 1 | 8 | 19 | 27 | 1 | 1.43 | 2 | 3.14 | 10 |
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| main.Term.mul(Factor) | 18.0 | 5.0 | 7.0 | 12.0 |
| main.Expression.add(Term) | 13.0 | 5.0 | 5.0 | 6.0 |
| main.Term.toString() | 13.0 | 3.0 | 9.0 | 10.0 |
| main.Term.derivative() | 11.0 | 5.0 | 4.0 | 6.0 |
| main.Expression.toString() | 9.0 | 3.0 | 6.0 | 7.0 |
| main.Expression.Expression(StringTool) | 6.0 | 1.0 | 4.0 | 4.0 |
| main.Term.mergeWith(Term) | 5.0 | 4.0 | 3.0 | 6.0 |
| main.Factor.make(StringTool) | 4.0 | 5.0 | 1.0 | 5.0 |
| main.Term.extractToExpression() | 4.0 | 4.0 | 4.0 | 5.0 |
| … | … | … | … | … |
| Total | 138.00 | 130.00 | 142.00 | 179.00 |
| Average | 1.77 | 1.67 | 1.82 | 2.29 |
从类的关系来看,各指标都基本低于阈值,符合高内聚低耦合的原则。
从代码复杂度分析数据可以看出Term.mul(Factor)方法复杂度超标了,原因是在里面对Factor进行判类并直接包办了所有乘法逻辑,这里的确应该将创建更多方法来分别办理不同种类Factor的乘法操作,不应该让该方法这样臃肿。
测试方法
本次作业延续使用了第一次作业的评测机,对于答案错误格式的判断主要依靠于sympy的sympify来判断,同时额外判断表达式因子是否后面跟了指数,这并不是完美的格式判定方式,也为第三次作业出错埋下伏笔
关于测评
本次作业没有在中测、强测和互测中出现bug。
互测时发现了两人共三个bug,其中两个是在优化时出现的错误,比较可惜
- 将相乘的表达式因子合并,没有注意到表达式因子不能有指数的格式规定
- 做了三角优化\(\sin^2(x)+\cos^2(x)=1\)但是如果仅有上式没有输出0而是输出了空串
- 没能解析
(x+1)*(x+1)*(x+1)
第三次作业
第三次作业我做的相当滑水,借助于第二次作业的良好架构,我只进行了少量的修改就完成了功能。而优化方面,合并同类项这件事变得比较复杂,我也没有追求完美的习惯,所以选择自暴自弃地放弃了所有合并化简。
测试方法
测试机仍然只需针对上一版本评测机进行少量的修改就可以完成针对所有Legal Format数据的生成。而在答案判断格式上,我仅采用了sympify的正确解析来评判格式,之所以没有在评判格式上下功夫是因为我对自己的输出模块很有信心,它在上一次作业中表现良好并且在这次作业中没有修改。最终我也因为自己的自信而付出了代价。
在互测开始之后,为了检测别人的程序输出是否有错误,我为评测机配备了输出格式检查,实现的方法其实很简单,只需要对自己的Java作业进行魔改,保留输入模块即可。现在也会后悔为什么自己没有对自己的程序做输出格式检查,如果做的了话是可以轻易的查出自己的错误的。
关于测评
本次作业在强测出现bug,原因是出现了答案中sin(x*x)的格式错误。
互测发现了两个人的bug
- 题目描述是指数不得超过50,有位同学认为指数50也是错的
- 对
-sin(x)**2求导时会多乘一个负号导致符号错误
心得体会
自动评测机应当先服务于自己的程序找bug,不应该作为杀人的工具。本来想做一匹狼人,结果却被猎人带走,真是后悔莫及。
写软件最忌讳的就是拍着胸脯说没问题放心用,那一定有问题。只有严谨的思考,高覆盖率的测试才是程序没问题的保证。
OO课让我第一次接触到设计模式这个概念,让我眼前一亮,这应该是程序员技能飞跃的一个阶段,从掌握各种复杂逻辑的写法,能够完成各种任务,到可以设计架构,做到高效开发,写出清楚明白的代码这样的飞跃。这真的是能让我稍稍提起兴趣了呢。


