BST(二叉搜索树)、AVL(平衡二叉树)、RBT(红黑树)的区别

一、二叉搜索树(BST：Binary Sort Tree)　　

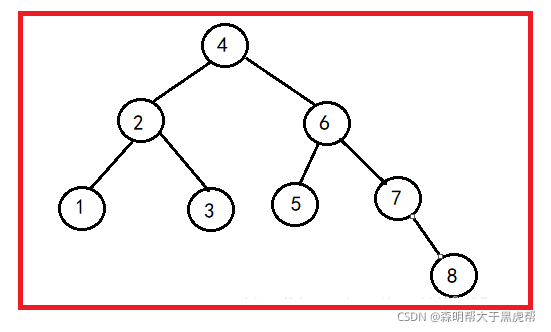
　　二叉查找树就是左结点小于根节点，右结点大于根节点的一种排序树，也叫二叉搜索树。

　　二叉查找树比普通树查找更快，查找、插入、删除的时间复杂度为O（logN）。但是二叉查找树有一种极端的情况，就是会变成一种线性链表似的结构。此时时间复杂度就变成了O（N），为了解决这种情况，出现了二叉平衡树。

　　

二、平衡二叉树(AVL：)　　

　　平衡二叉树全称平衡二叉搜索树，也叫AVL树。是一种自平衡的树。

　　AVL树也规定了左结点小于根节点，右结点大于根节点。并且还规定了左子树和右子树的高度差不得超过1。这样保证了它不会成为线性的链表。AVL树的查找稳定，查找、插入、删除的时间复杂度都为O（logN），但是由于要维持自身的平衡，所以进行插入和删除结点操作的时候，需要对结点进行频繁的旋转（缺点）。

　　

三、红黑树(RBT：RB-Tree)

　　红黑树是一种自平衡的二叉查找树，它的节点的颜色为红色和黑色。它不严格控制左、右子树高度或节点数之差小于等于1。也是一种解决二叉查找树极端情况的数据结构。

　　红黑树规定了：

　　　　1.节点是红色或黑色。

　　　　2.根节点是黑色。

　　　　3.每个叶子节点都是黑色的空节点（NULL节点）。

　　　　4 每个红色节点的两个子节点都是黑色。也就是说从每个叶子到根的所有路径上不能有两个连续的红色节点)。

　　　　5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。　　

　　

 

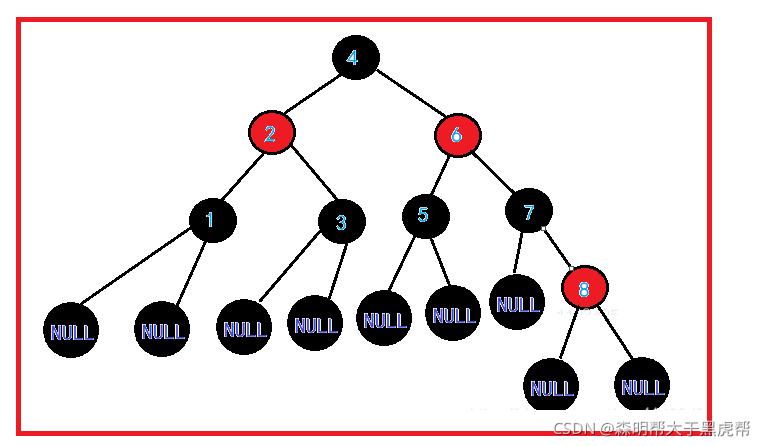
　　红黑树是保持“黑平衡”的二叉树：对于黑平衡是指，从根节点开始搜索，一直搜索到叶子节点，所经历的黑色节点的个数是一样的。

　　黑平衡二叉树，严格意义上，不是平衡二叉树：左右子树的高度差可能大于1，时间复杂度是O（logn），最大高度：2logn，红黑树不会像二分搜索树一样退化为链表。

 　　查找的时间上面会比AVL树慢一点，因为最大高度为2logn，添加操作和删除操作比AVL树要快一些：

　　

　　查找：

　　　　红黑树在查找方面和AVL树操作几乎相同。但是红黑树左右子树的高度差可能大于1，时间复杂度是O（logn），最大高度：2logn。（因为红黑树可以能确保树的最长路径不大于两倍的最短路径的长度，所以可以看出它的查找效果是有最低保证的。在最坏的情况下也可以保证O(logN)的，这是要好于二叉查找树的。因为二叉查找树最坏情况可以让查找达到O(N)。）

　　新增、删除：

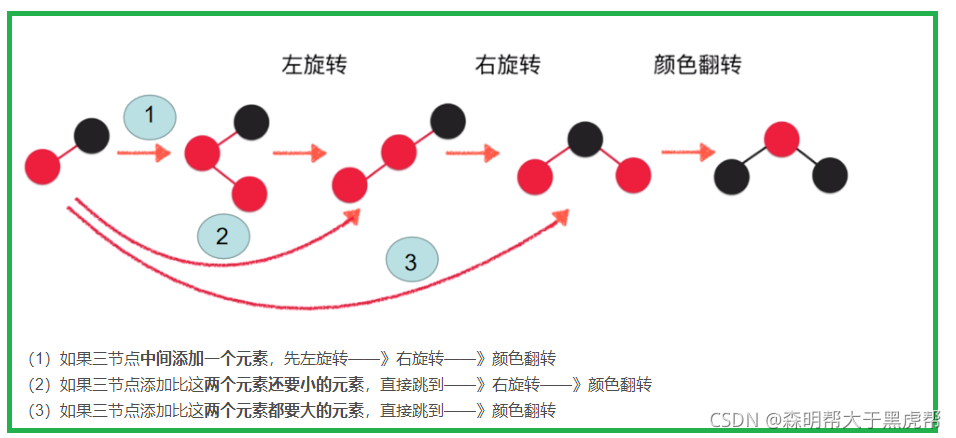
　　　　AVL树每次插入删除会进行大量的平衡度计算，红黑树是牺牲了严格的高度平衡的优越条件为代价，它只要求部分地达到平衡要求，结合变色，降低了对旋转的要求，从而提高了性能。（红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。）

四、RBT对比ALV

 　　AVL 和RBT 都是二叉查找树的优化。其性能要远远好于二叉查找树。他们之间都有自己的优势，其应用上也有不同。

　　1、结构对比

结构对比： AVL的结构高度平衡，RBT的结构基本平衡。平衡度AVL > RBT.

　　2、查找对比

查找对比： AVL 查找时间复杂度最好，最坏情况都是O(logN)。RBT 查找时间复杂度最好为O(logN)，最坏情况下比AVL略差。

　　3、插入删除对比

插入删除对比： AVL的插入和删除结点很容易造成树结构的不平衡，而RBT的平衡度要求较低。因此在大量数据插入的情况下，RBT需要通过旋转变色操作来重新达到平衡的频度要小于AVL。
　　如果需要平衡处理时，RBT比AVL多一种变色操作，而且变色的时间复杂度在O(logN)数量级上。但是由于操作简单，所以在实践中这种变色仍然是非常快速的。
　　当插入一个结点都引起了树的不平衡，AVL和RBT都最多需要2次旋转操作。但删除一个结点引起不平衡后，AVL最多需要logN 次旋转操作，而RBT最多只需要3次。因此两者插入一个结点的代价差不多，但删除一个结点的代价RBT要低一些。

　　4、使用上对比

使用上对比：
    数据分布较好：则比较宜于采用 AVL树(例如随机产生系列数);
    数据分布杂乱：如果你想处理比较杂乱的情况,则红黑树是比较快的。