matlab中使用dijkstra算法

matlab中使用dijkstra算法求最短路径

最近在搞数学建模，这个dijkstra算法搞r了好几天才明白，所以小菜鸡来记录一下。

来讲一下大概思路：
dijkstr算法整体是贪心算法思想
以这个无向图为例，假设从点1开始：

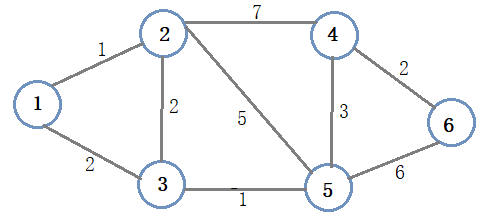
第一步：
创建一个邻接矩阵a[nxn]，a_ij表示两个节点的距离，对角线以及没有边的都为无穷大inf
第二步：
初始化一些变量
n表示结点的个数
u表示已经找到最短距离的结点下标，初始为1
p表示还未找到最短路径的结点下标数组，初始为[2,3,4,5,6]
d表示各点的当前最短距离，最终d里面存的是各点的最短距离，d(1)=0，其他的都为无穷大inf
v记录前一个到达该点的下标，初始都为0
第三步：
对p中的结点遍历，对于u(end)结点，（u(end)表示刚找到最短距离的那个结点，初始是1），比较d(u(end))和u(end)到该点(p中正在进行遍历的那点)的距离之和 与 源点到这点的距离(d(该点))，如果前者小，则替换d(该点)，并且替换v(该点)为u(end)
第四步：
在p中找到最短的d(p)，则该点已找到最短距离，（因为其他的d(p)都比它大，它不可能再通过其他中转结点到达这点的距离比这还小），更新u、p，回到第三步，直至所有u的长度等于n
第五步：
打印各个节点的最短距离和路径，路径遍历v即可，距离存在d

代码实现：

clc,clear
a = inf*ones(6);
a(1,[2,3])=[1,2];
a(2,[3,4,5])=[2,7,5];
a(3,5)=1;
a(4,[5,6])=[3,2];
a(5,6)=6;
a=min(a,a');
n=length(a);
u=1;    % 开始出发的结点下标
p=1:n; % 还未找到最短路径的结点下标
d=inf*ones(1,n); d(1)=0; % 各点的当前最短距离
v=zeros(1,n);    % 记录前一个到达该点的下标
while length(u) ~= n
    p=setdiff(p,u(end));
    for i=p
        if (d(u(end)) + a(u(end),i) < d(i))
            d(i) = d(u(end)) + a(u(end),i);
            v(i) = u(end);
        end
    end
    [tem, i] = min(d(p)); % tem是d(p)中最小的，i是取最小值时p向量的下标
    u = [u, p(i(1))];
end

for i=setdiff(1:n,u(1))
    disp("点"+u(1)+"到点"+i+"最短距离为："+d(i))
    disp("路径：")
    j=i;
    index=j;
    while v(j) ~= u(1)
        j=v(j);
        index=[j,index];
    end
    index=[u(1),index];
    disp(index)
end

运行结果：

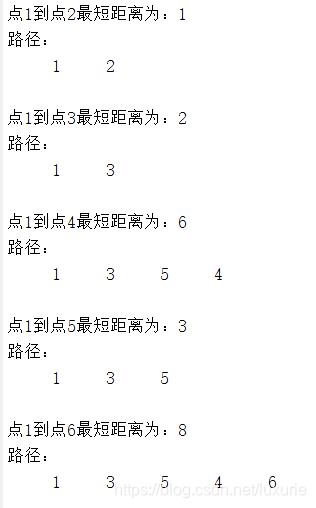
头大，好像理解还不是很透啊啊啊
end~