插值与拟合的简单介绍

插值与拟合

插值，给定一组数据，找到一条函数过所有的这些点。拟合，同样地，给定一组数据，找到一条尽可能接近这些点的函数，不要求点全在这条曲线上。

插值

有插值多项式法、分段插值法、三角插值法，常用的是前两种。

插值多项式

一般的插值多项式法是这样的，构造一个n阶多项式，其中有n+1个参数
$$Y(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n$$
把n+1组数据代入，得到有n+1个等式的方程组，提取系数矩阵，可以利用线性代数的知识求得唯一解。

当有很多组数据时，n就比较大，出现龙格现象。

比较著名的有拉格朗日多项式和牛顿插值法，由于这两个也有龙格现象，所以我们一般不用。

分段插值

分段插值就是用最近的几个点进行插值，是一个分段函数，造成了在节点处不够光滑的缺陷。

常用函数

还有一种埃尔米特（Hermite）插值，它不仅要求曲线全过这些点，还对一阶导数有要求，这时候我们可以唯一确定一个次数不超过 2n+1 的多项式。

单纯用Hermite插值，也会有龙格现象，因此我们用的比较多的一种时分段三次埃尔米特插值，对应matlab中的内置函数为p=pchip(x,y,new_x)，其中 x 是已知样本点的横坐标，y是已知样本点的纵坐标，new_x是要插入点的横坐标，可以是数或向量，返回值p是插入点的纵坐标。

例如：

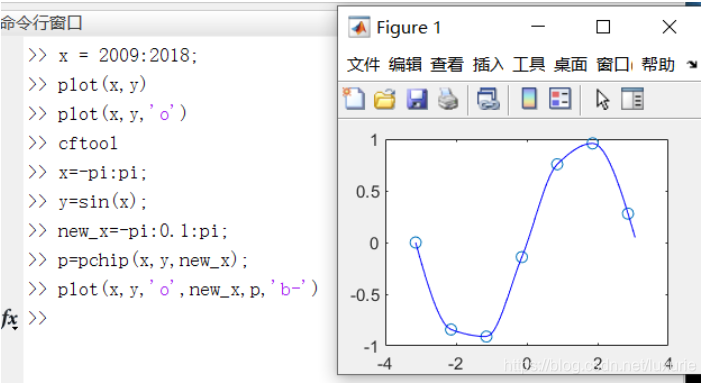
还有一种比较常用的三次样条插值，它要求二阶连续可微，对应的内置函数为 spline 参数、返回值与pchip函数相同。

例如：

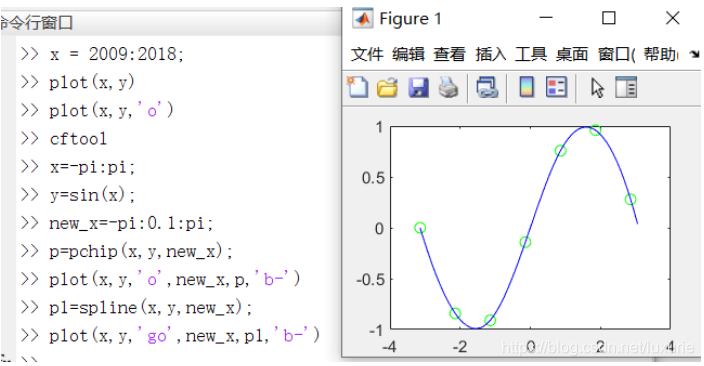
可以看出，三次样条插值得出的曲线更加光滑。

tips：插值可以用于短期预测。

拟合

常用的方法是最小二乘法。

总体平方和SST

误差平方和SSE

回归平方和SSR

当拟合曲线函数对参数线性时，SST=SSE+SSR，此时拟合系数$R^2$才有参考价值，非线性函数的误差一般看SSE即可。

另外，我们要灵活利用matlab的拟合工具箱，它不仅能直接拟合出图像、函数，还能生成代码。