【bzoj3209】: 花神的数论题 数论-DP

【bzoj3209】: 花神的数论题

首先二进制数中1的个数最多就是64个

设所有<=n的数里二进制中1的个数为i的有a[i]个

那么答案就是

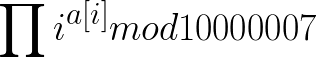 然后快速幂

求a[i]可以用DP

设在二进制中从高到低考虑到第k位，第k位之前的1的个数是cnt，n总共有len位

若第k位==1 那么 a[cnt+j]+=C(len-k,j) (j<=len-k)

其实就是前k-1位都与n前k-1位相等，第k位为0，后len-k随意选择j个1时对a的贡献

 1 /* http://www.cnblogs.com/karl07/ */
 2 #include <cstdlib>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <cmath>
 6 #include <algorithm>
 7 using namespace std;
 8 #define ll long long
 9 const ll p=10000007;
10 ll n,len;
11 ll c[65][65],a[65];
12 
13 ll Q_pow(ll x,ll y){
14     ll ans=1;
15     while (y){
16         if (y&1) ans=ans*x%p;
17         x=x*x%p;
18         y=(y>>1);
19     }
20     return ans; 
21 }
22 
23 int main(){
24     scanf("%lld",&n);
25     for (ll x=n;x;x=(x>>1)) len++;
26     for (int i=0;i<len;i++){
27         c[i][0]=c[i][i]=1;
28         for (int j=1;j<i;j++){
29             c[i][j]=c[i-1][j]+c[i-1][j-1];
30         }
31     }
32     int cnt=0,ans=1;
33     for (int i=len-1;i>=0;i--){
34         if (((n>>i)&1)){
35             for (int j=0;j<=i;j++){
36                 a[j+cnt]+=c[i][j];
37             }
38             cnt++;
39         }
40     }
41     a[cnt]++;
42     for (int i=1;i<=len;i++){
43         ans=ans*Q_pow(i,a[i])%p;
44     }
45     printf("%lld\n",ans);
46     return 0;
47 }
View Code

感觉写的自己都看不懂

posted @ 2017-03-26 03:46  karl07  阅读(224)  评论(0)  编辑  收藏  举报