【bzoj2186】: [Sdoi2008]沙拉公主的困惑 数论-欧拉函数

【bzoj2186】: [Sdoi2008]沙拉公主的困惑

考虑当 gcd(a,b)=1 则 gcd(nb+a,b)=1

所以[1,N!]与M!互质的个数就是

筛出[1,M]所有的素数p[i] 以及逆元 p[i]-1

处理一下前缀积inv[x]=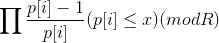

然后答案就是N!*inv[x]

 1 /* http://www.cnblogs.com/karl07/ */
 2 #include <cstdlib>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <cmath>
 6 #include <algorithm>
 7 using namespace std;
 8 #define LL long long
 9 const int N=1e7;
10 int R,T,n,m,cnt=0;
11 int jc[N+5],inv[N+5];
12 bool pr[N];
13 
14 void ex_gcd(int a,int b,int &x,int &y){
15     if (b==0) {x=1;y=0;return;}
16     ex_gcd(b,a%b,y,x);
17     y-=x*(a/b);
18 }
19 
20 int Inv(int a){
21     int x,y;
22     ex_gcd(a,R,x,y);
23     return (x%R+R)%R;
24 }
25 
26 void Jc(){
27     jc[0]=1;
28     for (int i=1;i<=N;i++){
29         jc[i]=1ll*jc[i-1]*i%R;
30     }
31 }
32 
33 void Prime(){
34     inv[1]=1;
35     for (int i=2;i<=N;i++){
36         inv[i]=inv[i-1];
37         if (!pr[i]){
38             inv[i]=1ll*inv[i]*Inv(i)%R*(i-1)%R;
39             if (1ll*i*i<=N) for (int j=i*i;j<=N;j+=i){
40                 pr[j]=1;
41             }
42         }
43     }
44 }
45 
46 int main(){
47     scanf("%d%d",&T,&R);
48     Jc();
49     Prime();
50     for (int i=1;i<=T;i++){
51         scanf("%d%d",&n,&m);
52         printf("%d\n",1ll*jc[n]*inv[m]%R);
53     }
54     return 0;
55 }
View Code

开long long跑的好慢。。11s卡过去

改成int 快了3s。。

水了一天数论感觉我数论还是这么辣鸡怎么办

posted @ 2017-03-19 23:27  karl07  阅读(157)  评论(0)  编辑  收藏  举报