你还在为级数角标而发愁吗？快看过来，这样做铁定不迷糊！

为什么级数的角标总是变来变去的？

  有的时候我们需要把级数进行一定的运算才能获取我们想要的结果，而在这些加减乘除运算中，级数的首项同样会跟整体一样进行着变化。

级数都有哪些运算？

  在我们考研的过程中，级数的运算有四则运算以及积分和求导。其中乘除运算在考研过程中并不要求。

级数的加减

  两级数相加减的前提就是角标要一致，在角标一致的前提下才能进行运算，而在题目中往往就是角标不一致的，那么如何化为角标一致就是关键问题了比如

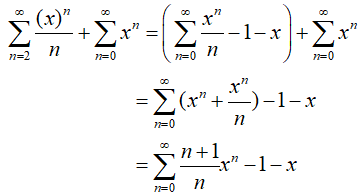
  这里我们通过补项的方式化为一致，当然其实在求和函数的时候在第二步就应该利用泰勒公式了。

  这里我们将x-1变换成了x这里的替换我相信会有一部分同学会迷糊，别着急我在下面就会分析这里到底怎么转换不迷糊

级数积分以及求导

  级数在积分和求导后各项都会发生变化，从而有可能导致级数的角标发生变化。

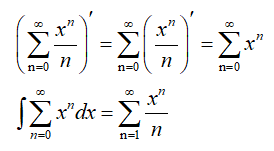
  我们能很清晰的发现，诶积分之后n怎么从1开始了。

要怎么理解才能不迷糊？

  其实我们不需要对角标来进行分析，我们只需要知道它首项在运算之后变成了什么，比如说，在积分时，首项1积分成了x那么自然的n就必须从1开始才是整个级数的首项了。而求导的话首项总是0次幂这时的n就仍然是0，铺垫了那么多其实就一句话：不要去管角标的变化，只要拿捏住首项自然级数的角标就不攻自破了。