EM算法索引

把这n个{试验结果来自B的概率}求和得到期望，平均后，得到B出正面的似然估计，同理有p和q。

重复迭代，直到收敛为止

http://blog.csdn.net/junnan321/article/details/8483343/

http://blog.csdn.net/zouxy09/article/details/8537620

http://www.hankcs.com/ml/em-algorithm-and-its-generalization.html

http://www.cnblogs.com/mindpuzzle/archive/2013/04/05/2998746.html

CNN
http://lib.csdn.net/article/deeplearning/50827

http://www.jianshu.com/p/606a33ba04ff

http://blog.csdn.net/abcjennifer/article/details/25912675

 

GMM:

http://www.cnblogs.com/CBDoctor/archive/2011/11/06/2236286.html(GMM聚类)

https://www.52ml.net/7890.html（Gmm01）

http://blog.csdn.net/sinat_22594309/article/details/65629407(gmm02)

 

EM算法二次整理：

1、对于含有隐变量的概率问题，不能直接使用最大似然函数解决的原因：运算上面最大似然函数中过多的加号，不能求解！

　　在推导EM算法之前，先引用《统计学习方法》中EM算法的例子：

　　例1. (三硬币模型) 假设有3枚硬币,分别记作A,B,C。这些硬币正面出现的概率分别为π，p和q。投币实验如下，先投A，如果A是正面，即A=1，那么选择投B；A=0，投C。最后，如果B或者C是正面，那么y=1；是反面，那么y=0；独立重复n次试验（n=10)，观测结果如下： 1,1,0,1,0,0,1,0,1,1假设只能观测到投掷硬币的结果，不能观测投掷硬币的过程。问如何估计三硬币正面出现的概率，即π，p和q的值。

  解：设随机变量y是观测变量，则投掷一次的概率模型为

　　有n次观测数据Y，那么观测数据Y的似然函数为

　　　　　　　　　　　　　　　　　　

  　　 那么利用最大似然估计求解模型解，即

　　　　　　　　　　　　　　　　　　

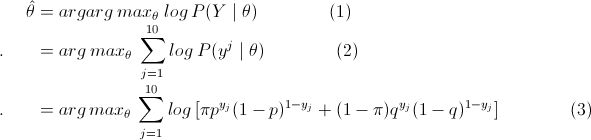
     　　 这里将概率模型公式和似然函数代入（1）式中，可以很轻松地推出 (1)=> (2) => (3)，然后选取θ(π,p,q)，使得（3）式值最大，即最大似然。然后，我们会发现因为（3）中右边多项式+符号的存在，使得（3）直接求偏导等于0或者用梯度下降法都很难求得θ值。

 　　　　这部分的难点是因为（3）多项式中+符号的存在，而这是因为这个三硬币模型中，我们无法得知最后得结果是硬币B还是硬币C抛出的这个隐藏参数。

那么我们把这个latent 随机变量加入到 log-likelihood 函数中，得

　　（  对于每一个样例i，让表示该样例隐含变量z的某种分布，满足的条件是。）

　　　　　　　　　　　　　　　　　　

 　　略看一下，好像很复杂，其实很简单，请容我慢慢道来。首先是公式（1），这里将zi做为隐藏变量，当z1为结果由硬币B抛出，z2为结果由硬币C抛出，不难发现

　　　　　　　　　　　　　　　　　　　　

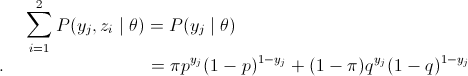
　　（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式

　　这个过程可以看作是对求了下界。对于的选择，有多种可能，那种更好的？

　　假设已经给定，那么的值就决定于和了。我们可以通过调整这两个概率使下界不断上升，以逼近的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需jensen不等式，需要让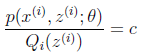：（那么对于每个样例的两个概率比值都是c）

　　　　c为常数，不依赖于。

　　　　对此式子做进一步推导，

，

 

　　　　至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。

　　　　已经不含有“+”符号了，并且本文认为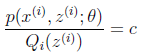：后， 建立的下界时可以认为   log(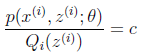)，这样就不存“+”问题了。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。