两个变量交换的三种方法的反汇编比较

先说结论：不开编译器优化的前提下，三变量交换法效率最高；开了优化后没区别。
起因：
学了点汇编的皮毛，想看看两变量交换的底层到底是怎么实现的。
主体代码：

//三变量交换法
int t = a;
a = b;
b = t;
//两减一加法
a = a + b;
b = a - b;
a = a - b;
//异或法
a ^= b;
b ^= a;
a ^= b;

用VS2017进行反汇编

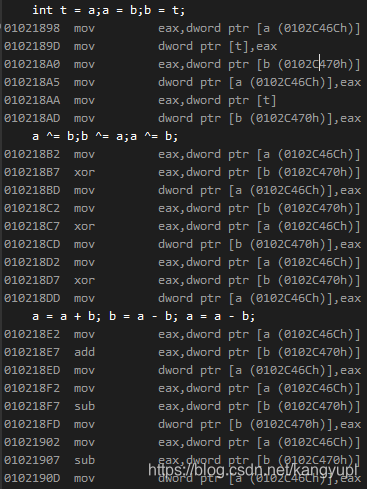
排版整理得

//三变量交换法
int t = a;a = b;b = t;
mov		eax,a  
mov		t,eax  
mov		eax,b  
mov		a,eax  
mov		eax,t  
mov		b,eax 

//两减一加法
a = a + b; b = a - b; a = a - b;
mov		eax,a  
add		eax,b  
mov		a,eax  
mov		eax,a  
sub		eax,b  
mov		b,eax  
mov		eax,a  
sub		eax,b  
mov		a,eax

//异或法
a ^= b;b ^= a;a ^= b;
mov		eax,a  
xor		eax,b  
mov		a,eax  
mov		eax,b  
xor		eax,a  
mov		b,eax  
mov		eax,a  
xor		eax,b  
mov		a,eax 

观察可知，每种方法都用到了六条mov指令，但后两种方法却还用到了其他的指令。
这打破了我的常规认知：用的变量越少，算法效率越高。
不，也不是完全推翻，毕竟后两种方法确实是减少了内存开销，有着更低的空间复杂度，虽然只有一个变量那么大。。。。。。这算是哪门子节约啊。

我原先觉得异或法最快，因为二进制操作快，因为计算机底层就是二进制运算。而且很多的初学者也是迷信二进制，这种对二进制效率的盲目认知使我写了的a ^= b ^= a ^= b,但我从来没有实验过。
那么接下来就实地测量一下：

#include <cstdio>
#include <iostream>
#include <windows.h>
using namespace std;
int a = 0,b=0;
void fun1() {
	for (int i = 0; i < 1000000000; i++) {
		int t = a;
		a = b;
		b = t;
	}
}
void fun2() {
	for (int i = 0; i < 1000000000; i++) {
		a = a + b;
		b = a - b;
		a = a - b;
	}
}
void fun3(){
	for (int i = 0; i < 1000000000; i++) {
		a = a ^ b;
		b = a ^ b;
		a = a ^ b;
	}
}
int main()
{
	a = 10;
	b = 12;
	long t1 = GetTickCount();
	fun1();
	long t2 = GetTickCount();
	fun2();
	long t3 = GetTickCount();
	fun3();
	long t4 = GetTickCount();
	cout << t2 - t1 << '\n' << t3 - t2<< '\n' << t4 - t3;
	return 0;
}

我的CPU是Core i5-6200U，windows系统，编译器是g++，跑出来的结果是

fun1: 2937
fun2: 5781
fun3: 5594

为了排除函数执行顺序的影响，我交换了三个函数的顺序又测试了两遍

fun3: 5703
fun1: 2875
fun2: 5891

fun2: 5937
fun3: 5703
fun1: 2844

结果很明显了，三变量交换法速度是另外两种方法的近乎两倍。

后记:
翻了CSDN，发现前人也思考过这个问题。有很多人说异或快，也有人说异或慢。但说快的一般都是拿二进制来说事，没有深入分析，甚至连测个速都没有。反观说异或慢的，深入至汇编，给出了严谨详细的证明，有理有据，令人信服。
譬如下面的二位前辈：
两个变量交换的扩展思考
用异或来交换两个变量是错误的

感想颇多，想说的也很多，但还是老祖宗看的透彻，一言以蔽之：

纸上学来终觉浅，绝知此事要躬行

原写于2019年06月17日 23:41:45