二叉树的定义
二叉树(Binary Tree)是n(n≥0)个元素的有限集合,该集合为空或者为由一个称为“根”的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成
二叉树的基本特点:
每个结点最多有两棵子树
左子树和右子树是有顺序的,且不可颠倒
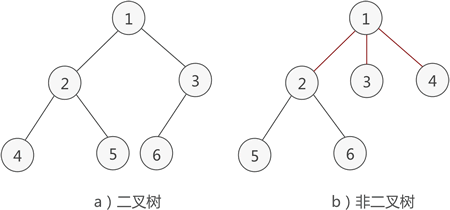
图一
节点、度和叶子的概念
1、结点
二叉树中的每一个元素都称为结点。通常二叉树的许多名词借用了家族关系
例如在上图中,2、3均是1的子结点,1是2&3的双亲,因而2、3互为“兄弟结点”
2、度
二叉树的度代表某个结点的孩子或者后继人的个数,1度表示只有一个孩子或者称之为单子树,2度是两个孩子或者说左右子树都有的二叉树。当然,二叉树某个结点的最大度为2.例如2的度数为2,3的度数为1
叶子
叶子是叶子结点的简称,叶子也就是leaf,原指网络结构中的某些计算机,它们从比较靠近中心的计算机处接收信号,而不把信号传至较远的计算机。在二叉树中叶子结点指树种处于最底端的结点,叶子结点没有子结点 例如上图中的 4、5、6均为叶子结点
特殊二叉树

图二
特殊二叉树有:满二叉树和完全二叉树
满二叉树:
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的一棵二叉树称之为满二叉树
例如图二中的第一张图,即为一棵满二叉树。而第二张图的B结点由于没有右子节树,所以不是满二叉树。
满二叉树的特点有:
>1.叶子**只能**出现在**最下**一层
2.非叶子结点的度**一定为2**
3.在同样深度的二叉树中,满二叉树的结点个数最多,叶子最多
完全二叉树一棵深度为k的有n个结点的二叉树,从树中的结点按从上至下、从左至右的顺序进行编号,如果编号为i(1≤i≤n)的节点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树,如图二的第三张图。
>1.叶子结点**只能**出现在**最下两层**
2.最下层的叶子若有结点,一定集中在**左下**部分
3.倒数第二层若有叶子结点,一定都集中在**右半**部分
4.如果结点度为1,则该结点**只有**左孩子,即不存在只有右孩子之说。
5.同样结点数的二叉树,完全二叉树的深度**最小**



