最大权闭合子图
最大权闭合子图
定义
闭合图:在一个图\(G=(V,E)\)中,若点集\(V\)中任意点连接的任意出弧,所指向的终点也在\(V\)中,则图\(G\)为闭合图。
对于一个有向图,每一个点都有一个权值(可以为正或负或0),选择一个权值和最大的子图,满足子图中每个点的后继结点也在这个子图里,这个子图就叫最大权闭合子图。
详解
解法:
-
先抽象出源点、汇点;
-
将权值为正的点和源点连接,边的容量为这个点的权值;
-
将权值为负的点和汇点连接,边的容量为这个点权值的绝对值;
-
然后除了源点、汇点之外的点原本怎么连就怎么连,且容量为无穷大;
-
最大权闭合子图权值 = 所有权值为正的点权值之和 - 以上构建的流网络的最小割(也即最大流)
详细描述如下:
首先有一个有向连通图\(G\),每个点带有一个权值,例如:
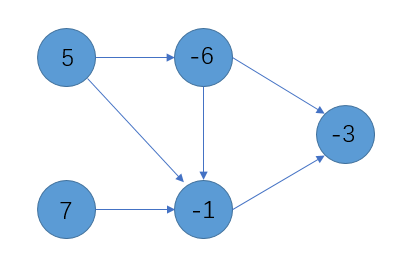
此时,构建一个源点\(s\),一个汇点\(t\),所有的点按权值的正负连接到\(s\)和\(t\)上,转换成一个边权值有向图,如下图:
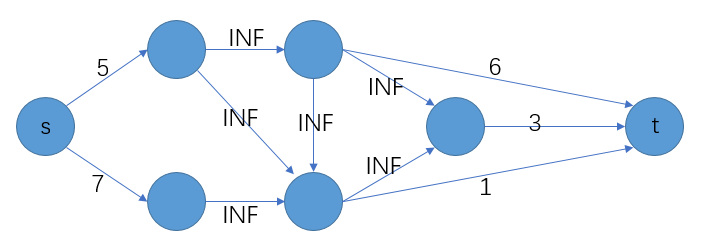
可以得出以下性质:
-
该流网络的最小割,是简单割;
简单割:割集中所有的边,都与\(s\)或\(t\)相连接。
显然的,因为不与连的边,权值都是INF,最小割不可能割在INF的边上;
-
该图中的每一个简单割产生的两个子图,我们记含有源点\(s\)的是图\(S\),\(S\)中属于原图\(G\)的结点和边(即去掉\(s\)和与\(s\)相连的边)构成图\(S'\),含有汇点\(t\)的是图\(T\),\(T\)中属于原图\(G\)的结点和边(即去掉\(t\)和与\(t\)相连的边)构成图\(T'\),则图\(S'\)是闭合图;
证明:① 简单割内不包含边权为INF的边,即割边不含有连通\(S'\)和\(T'\)的边;
② 流网络的割令图\(S\)中没有边与图\(T\)连通,又\(S'\in S, T'\in T\),则图\(S'\)中没有边与图\(T'\)连通;
那么,图\(S'\)所有的边都只能连接在\(S’\)之内,即为闭合图。
样例:
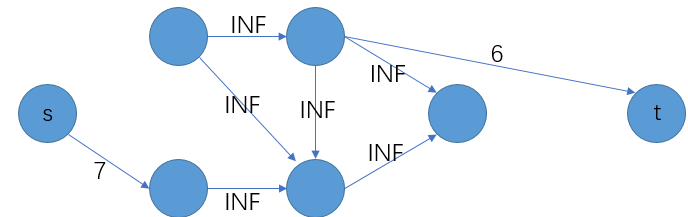
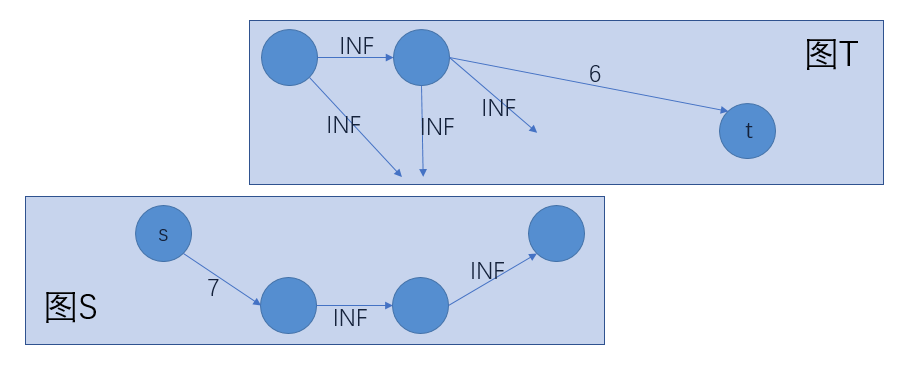
上图中,图\(S\)去掉\(s\)和容量为7的边即为图\(S'\),图\(T\)去掉\(t\)和容量为6的边即为\(T'\),显然图\(S'\)为原图\(G\)的一个闭合子图。
-
最小割产生的图\(S'\)为原图\(G\)的最大权闭合子图;
我们记割集中,所有连接在\(s\)上的边的权值和为\(x_1\),所有连接在\(t\)上的边的权值和为\(x_2\),而割集中所有边权值和为\(X=x_1+x_2\);记图\(S'\)中所有点的权值和为\(W\),记其中正权值之和为\(w_1\),负权值之和为\(-w_2\),故\(W = w_1 - w_2\);
则 \(W + X = w_1 - w_2 + x_1 + x_2\),由于\(x_2 = w_2\)(因为图\(S'\)中所有负权值的点,必然连接到\(t\)点,而图\(S'\)必然要与\(t\)分割开;故“割集中连接在\(t\)点上的边权值和”就是“图\(S'\)中所有负权值点的权值之和取负”),因而\(W + X = w_1 + x_1\);
显然的,\(w1 + x1\)是整个图\(G\)中所有正权值之和,记为\(sum\),故\(W=sum - X\),即 “图\(S'\)中所有点的权值和” = “整个图\(G\)中所有正权值之和” - “割集中所有边权值和”;
由于\(sum\)为定值,只要我们取最小割,则“图\(S'\)中所有点的权值和”就是最大的,即此时图\(S'\)为图\(G\)的最大权闭合子图;
最后,我们就有了求解这类问题的完整思路:
① 先记录整个图中,所有正点权值的和;
② 根据问题模型建立对应流网络,求最大流,最大流在数值上等于最小割,故我们得到了流网络的最小割;
③ “所有正点权值的和”减去“流网络的最小割”,即得最大权闭合子图的权值和。
修改自https://www.cnblogs.com/dilthey/p/7565206.html


