一个正整数表示为n个连续正整数之和（第1届第2题）

题目要求

       问题描述：一个正整数有可能可以被表示为 n(n>=2) 个连续正整数之和，如：

                           15=1+2+3+4+5

                           15=4+5+6

                           15=7+8

                       编写程序，根据输入的任何一个正整数，找出符合这种要求的所有连续正整数序列。 

       样例输入：15

       样例输出：1+2+3+4+5

                        4+5+6

                        7+8

解决方案

       题意很好懂，这个题第一直觉想到的是三重循环暴力破解，第一重控制序列起点，第二重控制序列元素个数，第三重输出符合题意的序列，但是显然，这样很费时，可不可以改进？可以！

       因为是连续的序列，考虑使用等差数列性质。

       对于等差序列，有三个关键的变量：一个是公差，一个是序列起点，另一个是序列长度。显然这序列公差为1，那么只考虑序列起点start和序列长度n。回味等差数列求和公式：

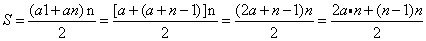
       由上面的公式可以得出下面的信息：

　　    1.将上式稍加变形，2S-(n-1)n=2a*n，即2S>(n-1)n>0。

           2.又2S=(2a+n-1)n，故：2S%n==0，(2S/n-n+1)%2==0。

           3.a=(2S/n-n+1)/2

       所以，可以考虑用控制序列长度的方式直接求出符合题意的序列起点，然后输出。

源码示例

 

结果展示

 

小结

       题目虽简单，但还是需要多加考虑，不要一上来就弄个三重循环...