拆分集合为相等的子集合(第1届第1题)
题目要求
问题描述:将1到N的连续整数组成的集合划分为两个子集合,且保证每个集合的数字和相等。例如,对于N=4,对应的集合{1,2,3,4},能被划分为{1,4}、{2,3}两个集合,使得1+4=2+3,且划分方案只有此一种。编程实现给定任一正整数N(1<=N<=39),输出其符合题意的划分方案数。
样例输入1:3
样例输出1:1 (可划分为{1,2}、{3})
样例输入2:4
样例输出2:1 (可划分为{1,3}、{2,4})
样例输入3:7
样例输出3:4 (可划分为{1,6,7}、{2,3,4,5},或{1,2,4,7}、{3,5,6},或{1,3,4,6}、{2,5,7},或{1,2,5,6}、{3,4,7})
解决方案
此题的解决方案有多种,但基本思想是动态规划。
首先,观察子集合的和。
对于任一正整数N,集合{1,2,3...N}的和为:
 ,
,
那么将集合S划分为两个和相等的子集合后,其子集合C中的整数和必为:
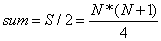 。
。
例如对于正整数4,集合{1,2,3,4}的和为S=4*(4+1)/2=10,那么将其划分为和相等的两个子集合后,其子集合C中的整数和为sum=S/2=5。
于是,此题就转化为在集合{1,2,3...N}中,任意选取k个数,使其和为N*(N+1)/4的问题,换句话说,就是限制子集合和为N(N+1)/4时,集合{1,2,3...,N}中可提供的整数选取方案数。
此描述隐含两个条件:第一,N*(N+1)除以4必须为整数,否则无法选取;第二,在选出k个数的所有方案中,每个方案都有其互补的方案。还是拿整数4举例,对于集合{1,2,3,4},任选k个数,使其和为4*(4+1)/4=5时,有两种方案{1,4}和{2,3},这两种方案互补构成所有整数集合,并生成一种集合划分方案。由此可得出,将选取k个数的所有方案数除以2,就是集合N划分为相等的子集合的方案数。
接下来,从集合S中往出选k个数,使其和为N*(N+1)/4,看有多少种选取方案。
给定集合S={1,2,3...,N},我们将其一字排开,挨个判断每个数是否应该加入到满足整数和为N*(N+1)/4的子集合C。对于每个数,要么可以被加入到集合C,要么不可以被加入,只有这两种可能。那么如何知道当前的整数是否应该加入子集合呢?由于这个子集合的和与单个整数大小有悬殊,我们似乎一眼看不出来。既然这样,我们不妨缩小问题规模来渐进考虑,而缩小问题规模的常见切入点是减小“自变量”的规模。
重读“接下来...”那句话,发现其中有两个条件,一个目的。目的是“有多少种选取方案”,这就是因变量。条件是“选出k个数”和“使其和为N(N+1)/4”,这就是两个自变量,一个限制选取的整数,另一个限制选出的整数的和。既然有了自变量和因变量,不如定义个函数出来更好的描述问题:
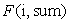
在函数F(i, sum)中,i代表当前需要判断集合S中第i个数是否应该加入子集合,sum代表此时限制的子集合整数和大小,F(i, sum)代表限制子集合整数和为sum时,集合{0,1,2...,i-1,i}中可提供的选取方案。(如果有点蒙,继续往下看,后面会附图...事实证明多看几遍就理解了...)
如果我们要减小自变量规模,就要从上面两个自变量下手。先看选取的整数,集合S中的最小整数是1,我们加入一个更小的整数0(显然,0不会影响集合的划分)来辅助思考。对于选出的整数的和,也就是限制的子集合的整数和,我们也从最小的0开始判断,那么问题的最小规模就是:限制子集合的整数和为0时,考虑整数0是否可以加入子集合?这个问题的答案是肯定的,当子集合的和为0时,完全可以将0加入,且仅有次一种方案,那么用上述函数来表达就是:
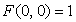
明白了此点,也就顺利地得出:F(0, 1)=F(0, 2)=F(0, 3)...=F(0, N)=0,因为限制子集合整数和大于0时,光有0无论如何也不能选出符合此限制的整数集合,即可行方案数为0。
迈出第一步,后面的就好办了...这是安慰人,事实是前方高能,更费心神!
为避免词语重复,下面说S中第i个元素时,就是指第i个整数。
假设此时,S中前i-1个元素都判断完了,紧接着应该判断第i个元素,与此同时,子集合的整数和被限定为sum,那么这第i个元素要不要被加入子集合呢?对此,我们做如下推断:
1:如果这第i个元素本身大于子集合的整数和sum,即i>sum,那么这第i个元素肯定不能加入子集合,否则就超出子集合整数和限制了。此时:F(i, sum)=F(i-1, sum),意思就是在相等的子集合整数和限制下,既然第i个元素没被加入,那么判断完第i个元素后的整数选取方案与判断完第i-1个数时的方案应该是相同的。
2:如果这第i个元素小于子集合整数和,那么就有两种考虑:
2.1:坚持不把第i个元素放入子集合,那么此时整数的选取方案仍然有F(i-1, sum)种。
2.2:如果把第i个元素放入了子集合,那么此时整数的选取方案有F(i-1, sum-i)种,sum-i的含义在于既然要放入第i个元素,就要给它留下足够的空间。F(i-1, sum-i)是在肯定要放入元素i的情形下,放入元素i前,整数的选取方案。
也即是说,i<=sum时,F(i, sum)=F(i-1, sum)+F(i-1, sum-i)。
综上可得:
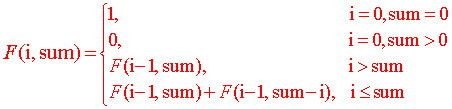
如果觉得这个式子还是比较蒙圈,那还是从具体的解决方案入手深化理解,毕竟理论都是抽象的,不好琢磨。
下面的解决方案中,我们均设定N=4,那么集合S={1,2,3,4}对应的最终子集合的整数和就是4*(4+1)/4=5,即求F(4, 5)的值。
解决方案一
先对可能出现的图例做说明:

图零:
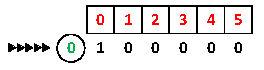
当对第0个元素判断时:
>若子集合整数和限定为0,那么只有把0放入子集合这一种可能。若子集合整数和大于0,那么放入0显然不能满足题意,故其选取方案均为0。
图一:

当对第1个元素判断时:
>限定子集合整数和为1:若要将元素1放入子集合,则1之前子集合中的元素和必须为1-1=0;若不放入元素1,则1之前子集合中的元素和必须为1,故在此子集合整数和限制下,加入1和不加入1就组成了两种方案,且这两种方案数的和为:F[1,1]=F[0,0]+F[0,1];
>限定子集合整数和为2:若要将元素1放入子集合,则1之前子集合中的元素和必须为2-1=1;若不放入元素1,则1之前子集合中的元素和必须为2,即:F[1,2]=F[0,1]+F[0,2];
>依次类推:F[1,3]=F[0,2]+F[0,3];F[1,4]=F[0,3]+F[0,4];F[1,5]=F[0,4]+F[0,5];
>注意最后:当选取的元素i(纵向)大于子集合整数和(横向)时,F[i, sum]=F[i-1, sum];也就是说,此时的元素i肯定放不进子集合,那么它满足题意的选取方案与上一个元素的方案一致。
图二:

图三:
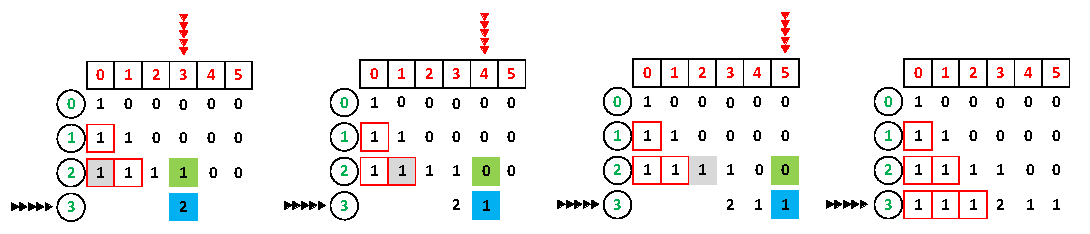
图四:

最后,右下角的值F[i, sum]反应了所有满足题意的子集合数,将其除以2才是集合S的划分方案数。
源码示例一

解决方案二
由上面的解释,不知道大家是否察觉到计算过程其实就是个递归过程,那么我们尝试将其转换为递归形式。
结合综述中的式子,递归应该是最好被理解的,但是递归的缺点就是计算太慢...
源码示例二

解决方案三
针对前面的叙述,换一个角度思考。
给定集合{0,1,2,3,4},如果我们是按顺序挑选的,那么要使选出的元素和为5,那么可以是选出元素和为5的组合,再把元素0加进来(如果之前的组合中没有0),还可以先选出和为4的元素组合,再把元素1加进来(如果之前的组合中没有1),或者,可以先选出和为3的元素组合,再把元素2加进来(如果之前的组合中没有2),再或者,可以先选出和为2的元素组合,再把元素3加进来(如果之前的组合中没有3)...最后,还可以是先选出和为0的组合,然后再把元素5加进来(如果之前的组合中没有5)。
如果用S(sum)表示元素和为sum的一个组合,那么上面的叙述可表示为:
S(5)=S(5)+0; S(5)=S(4)+1; S(5)=S(3)+2; S(5)=S(2)+3; S(5)=S(1)+4; S(5)=S(0)+5;
现在,再换一个维度考虑。
仍然是集合{0,1,2,3,4},如果我们按顺序挑选到了i,那么i可能成为S(0)到S(5)任一组合中的元素之一。
如果i成了S(5)中的一份子,那么S(5)的组成方案数必定是没加入i前S(5)已有的组成方案数加上加入i后S(4)的组成方案数。(定一定神,结合解决方案一考虑,每遍历到一个元素i,都要加上之前遍历过程中求出的解决方案数)。
下面上图...
图零:

当挑选到第0个元素时,显然,构成S[0]只有一种方案,就是把0放入,其他S[1]到S[5]均为0。
图一:

当挑选到第1个元素时,满足S[5]的方案数等于当前已有的方案数(没加入元素1之前)加上满足S[4]的方案数(加上元素1),依次类推。
这里可能有两个疑问,第一是当前已有的方案数(没加入元素1)从何而来?事实上,这个方案数自初始化以来,就一直"传递"下去,并在遍历到每个元素时,进行更新。另一个疑问是这里为什么倒着计算,即每遍历到一个元素,先从S[5]计算,其实是S[4...1]。这个原因在于每次更新数据前,当前位置保持的是遍历完上一个元素后的方案数,而计算当前遍历元素下的方案数时,总是需要用到遍历完上一个元素后的数据,所以,如果正着往后算,会造成数据错乱。(不知道我说清楚了没...)
举例,假如刚刚遍历完元素0,现在轮到遍历元素1了,此时上图数组的初始状态分别存储了遍历完元素0后满足子集合整数和为0、1、2、3、4、5的元素选取方案数。这个初始状态来自于上个元素,而且要被复用,所以必须等使用完了才能再根据当前元素1的情形进行更新。由于其复用的规律是后面用到前面的数据,所以从后往前推算就不会造成混乱了。
图二:

图三:

图四:

源码示例三

结果展示
小结
好了,再说下去我也快蒙圈了...
动态规划题型很多,需大量练习才能领会。其核心思想就是计算后面的结果时,利用之前的结果。当不能一眼看出题目中的递推关系时,不妨先找到题目的自变量去减小题目规模来逐步考虑,在考虑时,注意特殊情况的处理。
另外,将文字叙述变为公式推导也是重要的技能,唯有多练才可以掌握。
刚接触动态规划的同学可以从0-1背包问题看起,这里有篇文章或许能给你带来启发:0-1背包问题和部分背包问题分析


