7-10-有向网关键路径-图-第7章-《数据结构》课本源码-严蔚敏吴伟民版
课本源码部分
第7章 图 - 有向网关键路径
——《数据结构》-严蔚敏.吴伟民版
源码使用说明 链接☛☛☛ 《数据结构-C语言版》(严蔚敏,吴伟民版)课本源码+习题集解析使用说明
课本源码合辑 链接☛☛☛ 《数据结构》课本源码合辑
习题集全解析 链接☛☛☛ 《数据结构题集》习题解析合辑
本源码引入的文件 链接☛ Status.h、SequenceStack.c、ALGraph.c
文档中源码及测试数据存放目录:数据结构\▲课本算法实现\▲07 图\10 CriticalPath
概述
关键路径通常(但并非总是)是决定项目工期的进度活动序列,它是项目中最长的路径,即使很小浮动也可能直接影响整个项目的最早完成时间。
解析
用顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间的有向图叫AOE(Activity On Edge Network)网,在建筑学中也称为关键路线。AOE网常用于估算工程完成时间。
关键路径的算法建立在拓扑排序的基础之上,其计算方法简述为:
1.输入e条弧<j,k>,建立AOE-网的存储结构。
2.拓扑排序,并求得ve[]。从源点V0出发,令ve[0]=0,按拓扑有序求其余各顶点的最早发生时间ve[i]。如果得到的拓扑有序序列中顶点个数小于网中顶点数n,则说明网中存在环,不能求关键路径,算法终止;否则执行步骤3。
3.拓扑逆序,求得vl[]。从汇点Vn出发,令vl[n-1] = ve[n-1],按逆拓扑有序求其余各顶点的最迟发生时间vl[i]。
4.求得关键路径。根据各顶点的ve和vl值,求每条弧s的最早开始时间e(s)和最迟开始时间l(s)。若某条弧满足条件e(s) = l(s),则为关键活动。
注:此有向网使用了图的邻接表存储结构是为了方便进行拓扑排序。由于此处的邻接表存储结构中无结点的权值信息,故将有向网的权值信息放到了"弧的附加信息"中,也算是变通吧。当然,也可以通过修改原来的邻接表存储结构来应对此处的算法。
源码
文件一 ☛ CriticalPath.h

文件二 ☛ CriticalPath.c


文件三 ☛ CriticalPath-main.c (测试文档)

文件四 ☛ TestData_DG_AL.txt(有向网关键路径测试数据)

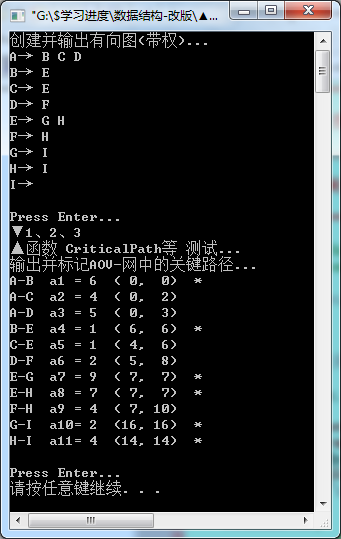
测试结果展示