对称二叉树

题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1. 二叉树；
2. 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的 id 表示节点编号。

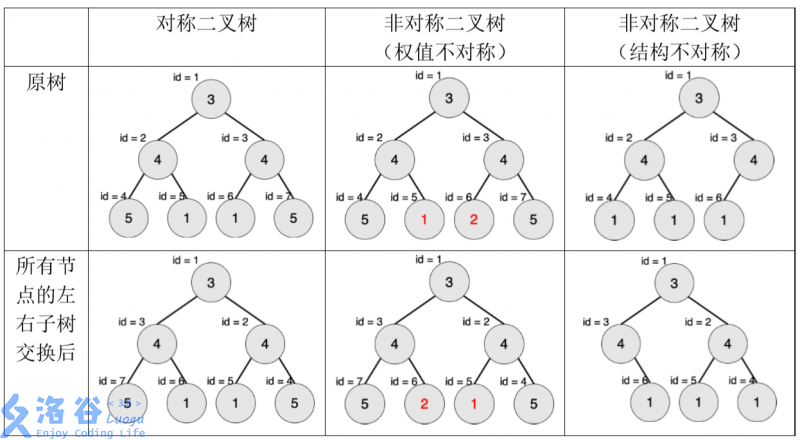
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数 最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点 T 为子树根的一棵“子 树”指的是：节点TT和它的全部后代节点构成的二叉树。

输入格式

第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号 1∼n，其中节点 1 是树根。

第二行 n 个正整数，用一个空格分隔，第 i 个正整数 v_i 代表节点 i 的权值。

接下来 n 行，每行两个正整数 l_i, r_i，分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子，则以 −1 表示。两个数之间用一个空格隔开。

输出格式

输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

输入输出样例

输入 #1

2 
1 3 
2 -1 
-1 -1 

输出 #1

1

输入 #2

10 
2 2 5 5 5 5 4 4 2 3 
9 10 
-1 -1 
-1 -1 
-1 -1 
-1 -1 
-1 2 
3 4 
5 6 
-1 -1 
7 8

输出 #2

3

说明/提示

【输入输出样例 1 说明】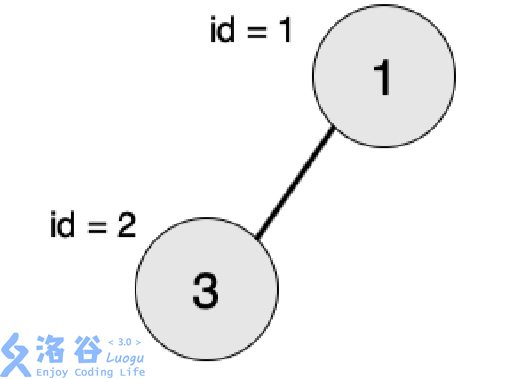

最大的对称二叉子树为以节点 2为树根的子树，节点数为 1。

【输入输出样例 2 说明】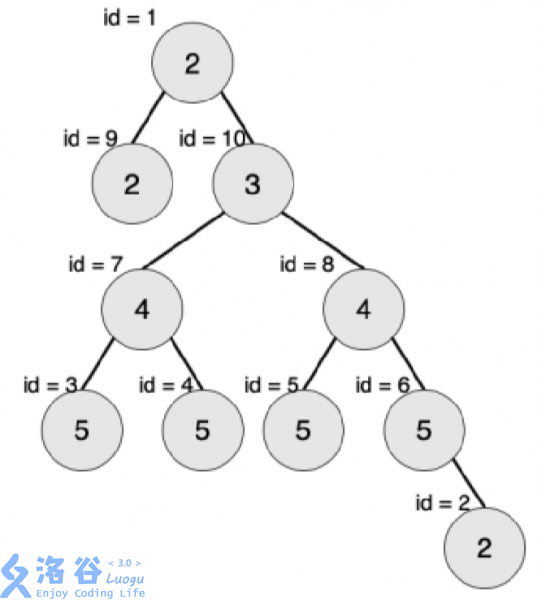

最大的对称二叉子树为以节点 7 为树根的子树，节点数为 3。

【数据规模与约定】
共 25 个测试点。
vi​≤1000。
测试点 1∼3,n≤10，保证根结点的左子树的所有节点都没有右孩子，根结点的右 子树的所有节点都没有左孩子。
测试点 4∼8,n≤10。
测试点 9∼12,n≤10^5，保证输入是一棵“满二叉树” 。
测试点 13∼16,n≤10^5，保证输入是一棵“完全二叉树”。
测试点 17∼20,n≤10^5，保证输入的树的点权均为 1。
测试点 21∼25,n≤10^6。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 1。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为 h，且二叉树有 2h−1 个节点，这就是满二叉树。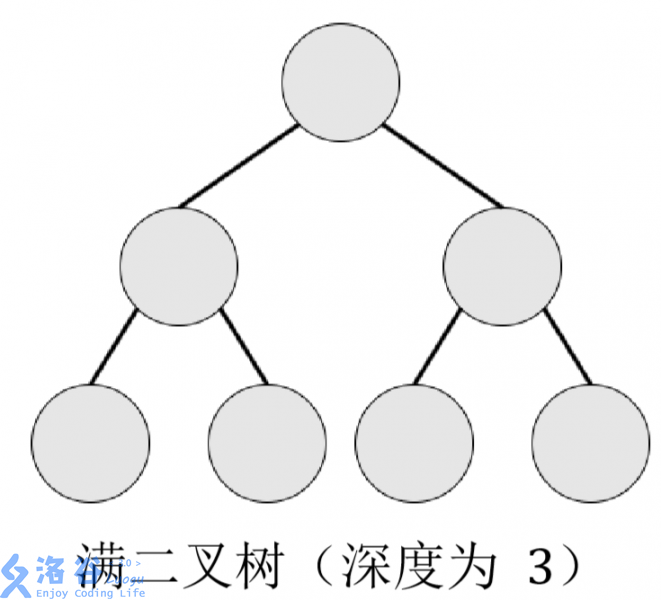

完全二叉树：设二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大 个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。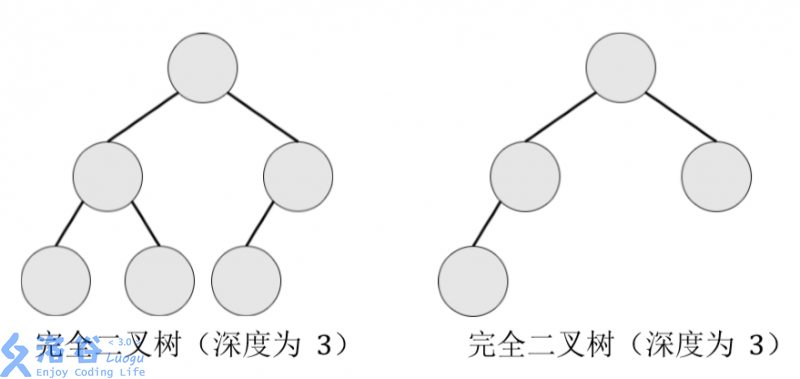

 

 

分析：

这道题真的是这几年最简单的PJ T4，但是我在考场上居然不会居然不会居然不会啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊！！！一道非常简单的DFS，随便搞搞就能过了。。。真没什么难度，只要会DFS的都会做吧。。。我真想杀一只去年的自己祭天。。。

 

CODE：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int M=1000005;
int n,ans;
struct node{
    int val,l,r;
}tr[M];
int size[M];
int get(){
    int res=0,f=1;
    char c=getchar();
    while (c>'9'||c<'0') {
        if (c=='-') f=-1;
        c=getchar();
    }
    while (c<='9'&&c>='0'){
        res=(res<<3)+(res<<1)+c-'0';
        c=getchar();
    }
    return res*f;
}
int dfs(int u){
    if (tr[u].l!=-1) size[u]+=dfs(tr[u].l);
    if (tr[u].r!=-1) size[u]+=dfs(tr[u].r);
    return size[u];
}
bool ok(int u,int v){
    if (u==-1&&v==-1) return true;
    if (u!=-1&&v!=-1&&ok(tr[u].l,tr[v].r)&&ok(tr[u].r,tr[v].l)&&tr[u].val==tr[v].val) return true;
    return false;
}
int main(){
    n=get();
    for (int i=1;i<=n;i++) tr[i].val=get(),size[i]=1;
    for (int i=1;i<=n;i++) tr[i].l=get(),tr[i].r=get();
    dfs(1);
    //for (int i=1;i<=n;i++) cout<<size[i]<<endl;
    for (int i=1;i<=n;i++)
        if (ok(tr[i].l,tr[i].r)) ans=max(ans,size[i]);
    printf ("%d\n",ans);
    return 0;
}