codeforces706E

好精妙的一道题啊

传送门：here

大致题意：有一个$ n*m$的矩阵，q次询问每次交换给定两个无交矩阵的对应元素，求操作后的最终矩阵？

数据范围：$ n,m<=1000, q<=10000$

模拟赛的时候考到类似的，当时很快想到对每行维护一个$ treap/splay$的优秀做法，

然后感觉复杂度一千万$ *log$甚至比暴力慢(事实证明确实如此)

正解其实又好写又快速，不过对我这种数据结构做傻的菜鸡来说考场上确实是想不到啊....

 

$ solution：$

对于每个元素维护两个指针R(右边的那个元素标号)以及D(下边的那个元素标号)还有这个点的元素值

注意元素从$ (0,0)$开始记录

对于每次修改，会发现只有矩阵边缘的点的指针需要被修改(如图所示)

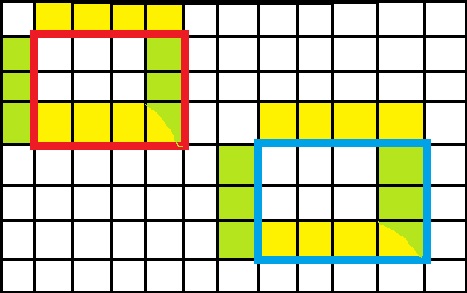
交换红蓝两个矩形时，只有涂黄色的格子下指针需要修改，涂绿色的格子右指针需要修改，对应swap一下即可

容易发现每次修改只有$ 2n+2m$格被修改了，因此总复杂度为$ O((n+m)q)$，非常优秀

（注意存图的时候第一行和第一列要空出来给空元素）

代码理解之后非常好写，以下是我的代码

#include<cstdio>
#include<iostream>
#define rt register int
using namespace std;
int i,j,k,m,n,x,y,z,cnt,p;
struct node{
    int v,D,R;//D表示下，R表示右 
}a[1100010];
int main(){
    scanf("%d %d %d",&n,&m,&k);n++;m++;
    for(rt i=1;i<=n;i++)
    for(rt j=1;j<=m;j++){
        int v=(i-1)*m+j;
        if(i>1&&j>1)scanf("%d",&a[v].v);
        if(i!=n)a[v].D=v+m;
        if(j!=m)a[v].R=v+1;
    }
    while(k--){
        int X1,Y1,X2,Y2,L,C,g1=1,g2=1,g3,g4;
        scanf("%d %d %d %d %d %d",&X1,&Y1,&X2,&Y2,&L,&C);
        while(--X1)g1=a[g1].D;while(--X2)g2=a[g2].D;
        while(--Y1)g1=a[g1].R;while(--Y2)g2=a[g2].R;
        g3=g1;g4=g2;
        for(rt i=1;i<=L;i++)g1=a[g1].D,g2=a[g2].D,swap(a[g1].R,a[g2].R);
        for(rt i=1;i<=C;i++)g1=a[g1].R,g2=a[g2].R,swap(a[g1].D,a[g2].D); 
        for(rt i=1;i<=C;i++)g3=a[g3].R,g4=a[g4].R,swap(a[g3].D,a[g4].D);
        for(rt i=1;i<=L;i++)g3=a[g3].D,g4=a[g4].D,swap(a[g3].R,a[g4].R);
    }
    int pla=a[a[1].D].R;
    for(rt i=1;i<n;i++,pla=a[pla].D){
        for(rt j=1,d=pla;j<m;j++,d=a[d].R)printf("%d ",a[d].v);
        putchar('\n');
    }
    return 0;
}