「CTSC2018」暴力写挂
毫无$ Debug$能力
全世界就我会被卡空间.jpg
题意
给定两棵树$ T,T'$,求一组点对$ (x,y)$使得$deep(x)+deep(y)-deep(LCA(x,y))-deep'(LCA'(x,y))$尽量大
$ x$可以等于$ y$,点数不超过$ 366666$,边有边权
$ Solution$
枚举$T'$的一个点$ u$作为$LCA'(x,y)$,则$ x,y$必然在$u$的不同子树或者就是点$u$
则
$ ans=max(ans,deep[x]+deep[y]-deep[LCA(x,y)]-deep[u])$
直接做复杂度过大
考虑$ deep[x]+deep[y]-deep[LCA(x,y)]=\frac{1}{2}(deep[x]+deep[y]+dist(x,y))$
这样有根树就转化成了无根树
考虑对$ T$边分,将$ T$转化成可边分二叉树之后建出边分树(可能不用完全建出来?)然后记录每个叶子节点的路径
比如树
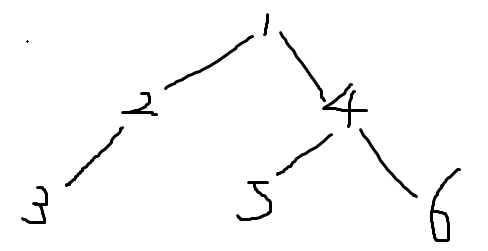
的其中一棵边分树为
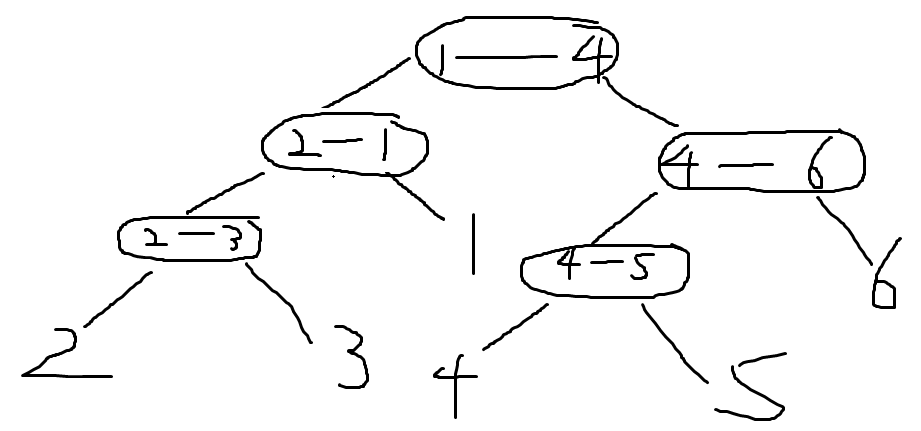
用一个$ 01$串记录到每个叶子节点的路径
边分树有两个优美的性质
1.边分树的深度是$ log(n)$级别的
2.边分树每棵子树中的叶子节点在原树上一定连通
如果一条路径经过了边分树上某条边节点
则这条路径一定为(边节点左边子树的某个点节点到边节点的左端点)+(边节点右边子树的某个点节点到边节点的右端点)+边长度
而每对点$ (x,y)$的贡献的两倍为$ deep[x]+deep[y]+dist(x,y)$
因此我们可以在每个节点记录(其子树内点节点到它的路径长度+该点深度)的最大值$ Max$
然后在每个边节点处处理贡献
一开始边分树中所有点节点尚未被"激活"因此所有节点的$ Max$值都是$ -INF$
如果一个点节点可被使用则将其激活,将这个点在边分树的位置到边分树的根的这段路经的所有$ Max$进行更新
并与途中统计答案
枚举$ T'$的每个节点
新建一棵空的边分树(即所有点节点都尚未被激活)
将其于$ T'$内的所有子节点"激活"并在过程中统计答案是一种可行做法
复杂度过大无法接受
容易发现边分树很像线段树可以动态开点插入
加上可以像线段树合并一样,这个点的边分树可以依次合并其所有子节点的边分树
并在过程中统计答案
复杂度大概是$ O(n log n)$的
(好像还是讲不太清楚啊...)
$ my \ code$
#include<ctime> #include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #include<queue> #include<vector> #define M 850010 #define rt register int #define ll long long using namespace std; namespace fast_IO{ const int IN_LEN=10000000,OUT_LEN=10000000; char ibuf[IN_LEN],obuf[OUT_LEN],*ih=ibuf+IN_LEN,*oh=obuf,*lastin=ibuf+IN_LEN,*lastout=obuf+OUT_LEN-1; inline char getchar_(){return (ih==lastin)&&(lastin=(ih=ibuf)+fread(ibuf,1,IN_LEN,stdin),ih==lastin)?EOF:*ih++;} } using namespace fast_IO; #define getchar() getchar_() inline ll read(){ ll x=0;char zf=1;char ch=getchar(); while(ch!='-'&&!isdigit(ch))ch=getchar(); if(ch=='-')zf=-1,ch=getchar(); while(isdigit(ch))x=x*10+ch-'0',ch=getchar();return x*zf; } void write(ll y){if(y<0)putchar('-'),y=-y;if(y>9)write(y/10);putchar(y%10+48);} void writeln(const ll y){write(y);putchar('\n');} int k,m,n,x,y,z,cnt,ans,la,p[M],lg2[M*2],up[20][M*2],q[M*2],tt,dt[M]; ll deep0[M],deep2[M/2]; struct node{int a,c;}; vector<node>e[M]; struct Tree{ int F[M],L[M],N[M*2],a[M*2],c[M*2],k=1; void dfs(int x,int pre,int id){ q[++tt]=x;p[x]=tt; for(rt i=F[x];i;i=N[i])if(a[i]!=pre){ if(id==0)deep0[a[i]]=deep0[x]+c[i]; else deep2[a[i]]=deep2[x]+c[i]; dt[a[i]]=dt[x]+1; dfs(a[i],x,id); q[++tt]=x; } } void add(int x,int y,int z){ a[++k]=y;c[k]=z; if(!F[x])F[x]=k; else N[L[x]]=k; L[x]=k; } void init(int x,int pre){ for(rt i=F[x];i;i=N[i])if(a[i]!=pre){ e[x].push_back({a[i],c[i]}); init(a[i],x); } } int LCA(int x,int y){ int L=p[x],R=p[y];if(L>R)swap(L,R);int len=lg2[R-L+1]; if(dt[up[len][L]]<dt[up[len][R-(1<<len)+1]]) return up[len][L];else return up[len][R-(1<<len)+1]; } void LCA_init(){ for(rt i=1;i<=tt;i++)up[0][i]=q[i]; for(rt i=1;i<=19;i++) for(rt j=1;j<=tt;j++) if(dt[up[i-1][j]]<dt[up[i-1][j+(1<<i-1)]])up[i][j]=up[i-1][j]; else up[i][j]=up[i-1][j+(1<<i-1)]; for(rt i=2;i<=tt;i++)lg2[i]=lg2[i>>1]+1; } ll dis(int x,int y){return deep0[x]+deep0[y]-2ll*deep0[LCA(x,y)];} }T0,T1,T2; void rebuild(){ for(rt i=1;i<=n;i++){ if(e[i].size()<=2){ for(auto j:e[i])T0.add(i,j.a,j.c*(j.a<=la)),T0.add(j.a,i,j.c*(j.a<=la)); continue; } int i0=++n,i1=++n;deep0[i0]=deep0[i1]=deep0[i]; for(rt j=0;j<e[i].size();j++)if(j&1) e[i0].push_back({e[i][j].a,e[i][j].c});else e[i1].push_back({e[i][j].a,e[i][j].c}); T0.add(i,i0,0);T0.add(i0,i,0);T0.add(i,i1,0);T0.add(i1,i,0); e[i].shrink_to_fit(); } } int id,nowmin,all,size[M]; bool vis[M]; void get(int x,int pre){ size[x]=1; for(rt i=T0.F[x];i;i=T0.N[i])if(!vis[i>>1]&&T0.a[i]!=pre){ get(T0.a[i],x);size[x]+=size[T0.a[i]]; const int now=abs(all-size[T0.a[i]]-size[T0.a[i]]); if(now<nowmin)nowmin=now,id=i; } } string path[M]; int ww=1; int ls[M],rs[M],L[M],R[M],top,len[M]; void solve(int x,int sz,int&it,string s){ if(sz==1)return path[x]=s,void(); nowmin=all=sz;if(!it)it=++ww; get(x,x);vis[id>>1]=1; int xx=T0.a[id],yy=T0.a[id^1],siz=size[xx]; L[it]=xx;R[it]=yy;len[it]=T0.c[id]; solve(xx,siz,ls[it],s+'0');solve(yy,sz-siz,rs[it],s+'1'); } struct tree{ int ls,rs;ll Max; }t[M*9]; int bb=0; void insert(ll &ret,int &x,int y,int pl,int id){//在第x棵树插入第y个点 if(!x)x=++bb,t[x].Max=-100000000000000ll; int sz=path[y].size(); if(pl==sz)return; if(path[y][pl]=='0'){ insert(ret,t[x].ls,y,pl+1,ls[id]); t[t[x].ls].Max=max(t[t[x].ls].Max,deep0[y]+T0.dis(y,L[id])); } else{ insert(ret,t[x].rs,y,pl+1,rs[id]); t[t[x].rs].Max=max(t[t[x].rs].Max,deep0[y]+T0.dis(y,R[id])); } ret=max(ret,t[t[x].ls].Max+t[t[x].rs].Max+len[id]); } int root[M]; int merge(ll &ret,int x,int y,int id){ if(!x)return y;if(!y)return x; t[x].Max=max(t[x].Max,t[y].Max); ret=max(ret,t[t[x].ls].Max+t[t[y].rs].Max+len[id]); ret=max(ret,t[t[y].ls].Max+t[t[x].rs].Max+len[id]); t[x].ls=merge(ret,t[x].ls,t[y].ls,ls[id]); t[x].rs=merge(ret,t[x].rs,t[y].rs,rs[id]); return x; } ll ret=-100000000000000ll; void calc(int x,int pre){ ll ans=-100000000000000ll; insert(ans,root[x],x,0,1); for(rt i=T2.F[x];i;i=T2.N[i])if(T2.a[i]!=pre){ calc(T2.a[i],x); root[x]=merge(ans,root[x],root[T2.a[i]],1); ret=max(ret,ans-2ll*deep2[x]); } } int main(){ la=n=read();t[0].Max=-100000000000000ll; for(rt i=1;i<n;i++){ x=read();y=read();z=read(); T1.add(x,y,z); T1.add(y,x,z); } for(rt i=1;i<n;i++){ x=read();y=read();z=read(); T2.add(x,y,z); T2.add(y,x,z); } T2.dfs(1,1,2);T1.init(1,1);rebuild(); tt=0;T0.dfs(1,1,0),T0.LCA_init(); int pl=1; solve(1,n,pl,""); calc(1,1);ret/=2; for(rt i=1;i<=la;i++)ret=max(ret,deep0[i]-deep2[i]); cout<<ret; return 0; }


