圆方树学习笔记
一直对联通分量不怎么了解
先开坑吧
$ tarjan$求割点
首先有一个性质：无向图的$ dfs$树没有横插边
搜索的时候判断每个孩子能否回到自己上方
若不可行则自己为割点
注意特判根节点：只要自己的不联通子树数量$ \geq 2$则一定是割点
$ tarjan$求点双连通分量
考虑$ tarjan$的时候
如果通过这个点的某子树推出自己是割点
那么从栈顶一直弹到把这个孩子弹出去再加上自己这个点一定构成点双连通分量
放张图吧
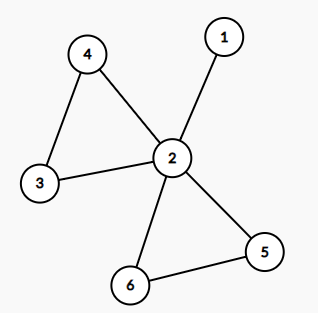
假设这张图的$ dfs$序是$1 2 3 4 5 6$
维护搜索栈：
$1 $
$1 、2$
$1 、2 、3$
$1 、2 、3 、4$
发现点双：$2 、3 、4$ 弹出$ 3 、4$
$1 、2、 5$
$1 、2、 5 、6$
发现点双：$2 、5 、6 $弹出$ 5、 6$
这样就找出了所有点双连通分量
构建圆方树
如果我们对于每一个点双连通分量以及大小为$ 2$的连通分量都新建一个点称为方点
把原图中的点称为圆点
先删除原图上所有边
对于每一个连通分量，我们把所有圆点往这个方点上连边
这样生成的树称为圆方树
如上图的圆方树为：
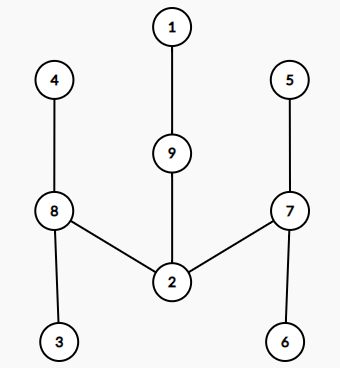
（请自行把点$ 7、8、9$脑补成方点）
圆方树的性质：
1.不存在圆点-圆点边以及方点-方点边
2.圆方树一定是一棵树
3.如果原图连通，构建出的圆方树也一定连通
应用：
$ 1.$求仙人掌任意两点间最短路：BZOJ 2125
直接构建圆方树，圆点到方点的距离为这个圆点到这个方点父亲的圆点在原图上的最短距离
每次询问求出$ LCA$，若$ LCA$是圆点则直接求路径权值和
若$ LCA$是方点则跳到$ LCA$下面的圆点，然后求一下环上最短路即可
$ 2.$求从$ x$走到$ y$的路径上可能经过的最小点权，带修改 UOJ #30
如果两个点经过了某个连通分量，一定可以走到这个连通分量的最小值
直接构建圆方树，圆点存点权，方点用$ multiset$存连通分量的点权集合
通过一些巧妙的操作来减小修改的复杂度
$ 3.$求数对$(x,y,z)$的数量使得满足存在一条$x$到$z$的路径上经过$y$，要求$x,y,z$两两不同 APIO2018 铁人两项
直接构建圆方树，令圆点权值为$ -1$，方点权值为$ size(点双大小)$，然后直接在树上做就好了
