min25筛入门
首先我们来看一下模板题:传送门
大致说一下题意:给定一个积性函数$f(x)$,求$\sum_{i=1}^{n} f(i)$,其中$f(p^k)=p^k(p^k-1)$,p是质数,k是任意正整数。
我了不引起歧义,我们在这里事先说明一下如果没有特殊声明,符号所代表的意义请在这里查询:
$P$代表质数的集合。
$p$代表任意质数。
$k$代表任意正整数。
这篇文章里我们认为1既不是质数,也不是合数!
概括min25筛适用的形式:给定一个积性函数,其中$f(p^k)$是一个关于$p^k$的多项式(项数越少,算法就越快。否则没有复杂度保证。因此我们可以在这里换种说法:min25筛只适合$f(p^k)$是关于$p^k$的低阶多项式。具体多低可以根据题意来看)。
我们考虑多项式的特殊情况:单项式。多项式可以拆成若干个单项式来计算。我们看下面的例子。
假设我们这个函数是模板题中的那个函数。也就是说$f(p^k)={p^k}^2-p^k$,我们可以设$g_1(p^k)=p^k$,$g_2(p^k)=(p^k)^2$。这样一来$f(p^k)=g_2(p^k)-g_1(p^k)$。
现在我们把问题转化为了$f(p^k)$是一个形如$(p^k)^i$的式子,其中i是任意正整数,且$f(x)$是一个积性函数。求$f(x)$的前缀和.
Part 1 问题的转化
我们很容易的想到:对于求和的式子,看起来如果没有优化的办法了,我们可以像FFT那样先分项再合起来。
对于这个积性函数,我们很容易发现质数和其有莫大的关联。
因此按是否为质数分类:前面为质数,后面为合数
$\sum_{i=1}^{n} f(i)=\sum_{i\in P}^nf(i)+\sum_{i=1|i\notin P }^nf(i)$
然后我们考虑莫比乌斯反演和狄利克雷卷积常用的那一套:改变枚举的东西。
对于后面那部分,我们枚举最小的质因子$p$和最小质因子的指数$k$。这里有一个性质:所有合数的最小质因子一定小于$\sqrt n$。(比较显然,可以用反证法证明)
注意:minj表示j的最小质因子。
$=\sum_{i\in P}^nf(i)+\sum_{i\leq p^k\leq n,1< p< \sqrt n}^nf(p^k)(\sum_{1\leq j \leq \frac{n}{p^k},minj>p}f(j))$
我们观察后面变成了什么:
我们枚举了最小的质因子$p$和最小质因子的指数$k$,对于任意$1\leq j \leq \frac{n}{p^k}$的j,只要它的最小质因子比目前枚举的最小质因子p大,就代表$f(jp^k)$的最小质因子是p,并且由于积性函数$f(xy)=f(x)f(y),gcd(x,y)=1$的性质,我们知道$f(jp^k)=f(p^k)f(j)$。根据乘法分配律我们可以把所有的合法的$f(j)$加起来后统一和$f(p^k)$相乘。
由于$f(p^k)$可以直接求出来,所以实际上我们现在式子变成了仅仅要求两部分而不是三部分:
1.所有质数的f()的和。
2.枚举最小质因子后,求最小质因子大于这个质因子所有的f()的和。
至此。问题转化完毕。如何求它是一个俄罗斯大佬提出来的在$O(\frac{n^{\frac{3}{4}}}{log_2n})$时间复杂度下完成它的算法。
Part 2 求所有小于n的质数p的$f(p)$的和
当n处于1e10的数据强度的时候,线性筛时空复杂度都不能接受。这种似乎穷途末路的时候我们的好朋友dp(或许是递推?)给我们指明了方向。
设$g(n,i)$表示从1到n所有满足以下条件之一的数的k次方和。(其中这里的k就是我们刚开始时谈到的多项式转化为单项式时那个项的幂。为了方便,我们暂时假设k=0。k=0可以认为统计的是$k^0=1$也就是个数)
1.是质数 2.最小质因子大于$p_i$(其中$p_i$可是视为0)
根据定义我们可以发现,$g(n,0)$就是1~n的k次方和。
然后我们考虑转移,先给出转移方程:$g(n,j)=g(n,j-1)-p_j^k(g(\frac{n}{p_j},j-1)-g(p_{j-1},j-1))$
分析转移方程之前。我们首先思考转移的意义:
对于$g(n,j)$和$g(n,j-1)$,他们两个状态中所包含的数相比较之下的不同之处仅仅在于$g(n,j)$不包含最小质因子恰好为$p_j$的合数。
其中$g(p_{j-1},j-1)$因为1~$p_{j-1}$中不可能存在满足条件2的数,所以可以理解为这是1到$p_{j-1}$之间的质数个数。
我们可以从n个数中提取出一个最小质因子$p_j$,$g(\frac{n}{p_j},j-1)$的意义是1~$\frac{n}{p_j}$中质数的个数+合数的最小质因子大于$p_{j-1}$的个数。
由于我们最小质因子的最大值不会超过$\sqrt n$,所以$\frac{n}{p_j}$一定大于枚举的最小质因子$p_j$。
因此(1~$\frac{n}{p_j}$中质数的个数+1~$\frac{n}{p_j}$中合数的最小质因子大于$p_{j-1}$的个数)=(1~$p_{j-1}$中质数的个数+$(p_{j-1}+1)$~$\frac{n}{p_j}$中质数的个数+1~$\frac{n}{p_j}$中合数的最小质因子大于$p_{j-1}$的个数)。
因此$(g(\frac{n}{p_j},j-1)-g(p_{j-1},j-1))$的意义就是(1~$p_{j-1}$中质数的个数+$(p_{j-1}+1)$~$\frac{n}{p_j}$中质数的个数+1~$\frac{n}{p_j}$合数的最小质因子大于$p_{j-1}$的个数)-(1~$p_{j-1}$之间的质数个数)=($(p_{j-1}+1)$~$\frac{n}{p_j}$中质数的个数+1~$\frac{n}{p_j}$中合数的最小质因子大于$p_{j-1}$的个数)。
而($(p_{j-1}+1)$~$\frac{n}{p_j}$中质数的个数+1~$\frac{n}{p_j}$中合数的最小质因子大于$p_{j-1}$)的个数正好是最小质因子大于$p_j$的所有可能的数个数。
因此当k不等于0的时候,$p_j^k*(g(\frac{n}{p_j},j-1)-g(p_{j-1},j-1))$就是最小质因子恰好为$p_j$的合数的贡献。
转移方程我们分析完毕
Part 3 求解答案
之前说的那么详细,现在就可以简略说了。因为求解答案的思想和g数组一样也是dp
设S(n,x)表示求1到n中所有最小质因子大于p_x的函数值之和,注意这里是f而不是k次方。答案就是S(n,0)。
我们将满足条件的数分成两部分,第一部分是大于p_x的质数,也就是g(n)-sp_x,另一部分是最小质因子大于p_x的合数,枚举最小质因子:
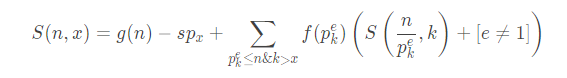

以上为时间复杂度的对比,可以看出在随机大数据的范围下,min25筛跑的比杜教筛还要理想。



