《数据库系统》：关系数据库设计

关系数据库设计

关系数据库设计的目的是得到一组合适的关系模式，使其不含冗余，结构良好，便于获取信息。

概念和数学基础

码

• 超码：一个或多个属性的集合，这个集合可以唯一地区分出一个元组（一行）
• 候选码：包含属性最少的超码，可能有多个
• 主码：人为地选中，作为一行的区分标准的候选码。本节中候选码更常用
• 另一个常用的码是外码，与本节无关，不详细介绍

函数依赖

函数依赖是一个形如 \(\alpha\rightarrow\beta\) 的逻辑推理式，表示属性集 \(\alpha\) 决定(determine)属性集 \(\beta\) ，或称 \(\beta\) 依赖 \(\alpha\) . 同一模式中包含的多条函数依赖称为函数依赖集。

例如，\(R\) 上的两个属性 \(\alpha\) 和 \(\beta\) ，如果关系实例中的所有元组对 \(t_1，t_2\) 都符合 若 \(t_1[\alpha]=t_2[\alpha]\) ，则 \(t_1[\beta]=t_2[\beta]\)。也就是说，只要我们知道 \(\alpha\) 的值，就能唯一确定 \(\beta\) 的值，称 \(\alpha\) 决定 \(\beta\) 。特别地，如果\(\beta\subseteq\alpha\)，称为平凡的函数依赖。

由此，我们得出超码的新定义：对于关系R和函数依赖集K，若 \(K\rightarrow R\) 在 \(r(R)\) 上成立，则 \(K\) 是 \(r(R)\) 的一个超码。

闭包

有了函数依赖集F，我们就可以由已知的函数依赖得出其他的函数依赖。如 \(r(A, B, C)\)中有\(A \rightarrow B, B \rightarrow C\)，则 \(A \rightarrow C\)（具体推理方法见下文Armstrong公理）。类似的推理被称为逻辑蕴涵。不断将这些新的函数依赖加入F，最终能够得到一个被原F逻辑蕴涵的所有函数依赖的集合，称为F的闭包，记作 \(F^+\).

Armstrong公理系统

反复运用以下三条Armstrong公理，就能通过\(F\)求出\(F^+\)，保证结果是正确有效的。

• 自反律：若\(\alpha\)为一属性集，\(\beta\subseteq\alpha\)，则\(\alpha\rightarrow\beta\)
• 增补律：若\(\alpha\rightarrow\beta\)，\(\gamma\)为一属性集，则\(\gamma\alpha\rightarrow\gamma\beta\)
• 传递律：若\(\alpha\rightarrow\beta\)且\(\beta\rightarrow\gamma\)，则\(\alpha\rightarrow\gamma\)

Armstrong公理是完备的。下面还有一些推论规则，使用起来更方便。

• 合并律：若\(\alpha\rightarrow\beta\)且\(\alpha\rightarrow\gamma\)，则\(\alpha\rightarrow\beta\gamma\)
• 分解律：若\(\alpha\rightarrow\beta\gamma\)，则\(\alpha\rightarrow\beta\)且\(\alpha\rightarrow\gamma\)
• 伪传递律：若\(\alpha\rightarrow\beta\)且\(\gamma\beta\rightarrow\delta\)，则\(\alpha\gamma\rightarrow\delta\)

属性闭包

与函数依赖集的闭包相似，属性闭包是某一属性（或属性集）决定的所有属性的集合。函数依赖集F下被属性\(\alpha\)决定的所有属性的集合称为\(F\)下\(\alpha\)的闭包，记为\(\alpha^+\).

利用属性闭包，我们可以判断属性\(\alpha\)是否为超码，通过所有属性集的闭包求\(F^+\)，求候选码等。

无关属性

一条函数依赖中可能含有不必要的属性，“不必要”指的是去掉这些属性不会改变函数依赖集的闭包。下文将举例说明，并提供找出无关属性的方法。

关系模式 \(student(sid, name, birthday, dept\_name)\)，显然有\(sid→name，sid→dept\_name\)...根据Armstrong公理能写出很多函数依赖，但我们只用几条为例。以这两条函数依赖作为F。结合实际生活经验，我们还能得出两条函数依赖：\(sid,name→dept\_name，sid→name,dept\_name\) ，尽管它们看起来有些臃肿。

“臃肿”是因为这些函数依赖不必要单独列出，利用F中的函数依赖，运用Armstrong公理就能推导。
F中的函数依赖告诉我们，属性sid决定dept_name。根据增补律，sid与任意属性构成的集合都能决定dept_name，因此这里的name是无关属性。同样，根据合并律也能得出sid→name,dept_name，因此这里的name或dept_name其中一个是无关属性。

在函数依赖\(\alpha\rightarrow\beta\)中：

如果\(A\in\alpha\)且\(F\)逻辑蕴涵\((F-\{\alpha\rightarrow\beta\}\cup\{(\alpha-A)\rightarrow\beta\})\)，则属性\(A\)在\(\alpha\)中是无关的。

如果\(A\in\beta\)且\((F-\{\alpha\rightarrow\beta\}\cup\{\alpha\rightarrow(\beta-a)\})\)逻辑蕴涵\(F\)，则属性\(A\)在\(\beta\)中是无关的。

通俗来说：

在函数依赖\(\alpha\rightarrow\beta\)中：

要证明\(\alpha\)中的属性A是无关的，就看能否利用F推出\((\alpha-A)\rightarrow\beta\). 如果能，A就是无关属性。

要证明\(\beta\)中的属性A是无关的，就从F中去掉\(\alpha\rightarrow\beta\)，加上\(\alpha\rightarrow(\beta-a)\)，看能否推出F. 如果能，A就是无关属性。

正则覆盖

F的正则覆盖\(F_c\)是最小的、与F等价的函数依赖集。同一函数依赖集对应的\(F_c\)可能不唯一。\(F_c\)具有如下性质：

• \(F_c\)中的任何函数依赖都不含无关属性
• \(F_c\)中函数依赖的左半部分\(\alpha\)都是唯一的

\(F_c\)的计算方法如下：

使用合并律将\(F_c\)中所有形如\(\alpha_1\rightarrow\beta_1, \alpha_1\rightarrow\beta_2\)的依赖替换为\(\alpha_1\rightarrow\beta_1,\beta_2\)

验证\(F_c\)中的每一条函数依赖，消除其中的无关属性，同时不断更新\(F_c\)

多值依赖

在了解多值依赖前，建议读者先阅读下面的1NF, 2NF, 3NF, BCNF部分。

函数依赖理论能够将关系模式分解为BCNF，但它仍有不足。考虑教师模式 \(teacher(ID, child, phone)\)，它符合BCNF，但仍然会出现冗余，因为一个教师可以有多个手机号码，也可以有多个孩子，导致同一教师在表中有多个对应元组。为了消除冗余，可以将其分解为 \(r_1(ID,child),r_2(ID,phone)\). 这个分解虽然看起来合理，但在函数依赖中并没有理论依据。为了解决这类问题，引入多值依赖。

根据函数依赖的定义，它说明了哪些元组不能存在于关系中；与之相对，多值依赖规定了哪些元组应当存在于关系中。

\(\alpha\rightarrow\rightarrow\beta\) 称为\(\alpha\)多值决定\(\beta\). 它在R上成立的条件是：

在关系\(r(R)\)中任意一对满足\(t_1[\alpha]=t_2[\alpha]\)的元组对\(t_1,t_2\)，\(r\)中都存在元组\(t_3,t_4\)，使得：

\(t_1[\alpha]=t_2[\alpha]=t_3[\alpha]=t_4[\alpha]\)
\(t_3[\beta]=t_1[\beta],t_4[\beta]=t_2[\beta]\)
\(t_3[R-\beta]=t_2[R-\beta],t_4[R-\beta]=t_1[R-\beta]\)

多值依赖具有以下两条性质：

对于\(\alpha,\beta\subseteq R\):

若\(\alpha\rightarrow\beta\)，则\(\alpha\rightarrow\rightarrow\beta\) ； 若\(\alpha\rightarrow\rightarrow\beta\)，则\(\alpha\rightarrow\rightarrow R-\beta\)

只看定义有些难以理解。依然以模式\(teacher(ID, child, phone)\)为例，假设该表如下所示：

ID	child	phone
01	Mike	12345
01	Bob	12666
02	Joy	23456
02	Kim	23456
02	Kim	23666

目前，该模式不符合\(ID\rightarrow\rightarrow child\)，也不符合\(ID\rightarrow\rightarrow\ phone\)（由性质2可知这两条依赖是等价的）。

要满足多值依赖，属性（集）间必须形成完全二分图（也是笛卡尔积）。如图所示：

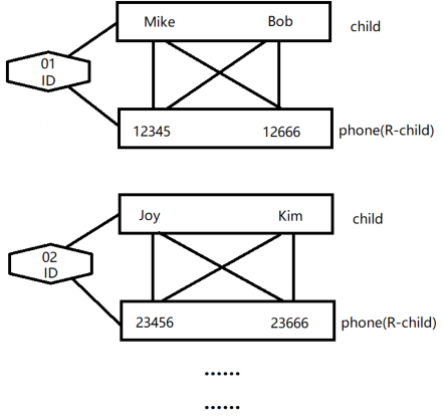
由图可知，上表还需要添加\((01,Mike,12666),(01,Bob,12345),(02,Joy,23666)\)三个元组，以满足多值依赖。由此看来，满足多值依赖就能够保证数据的完整性（但仍会出现冗余）

我们用D表示函数依赖和多值依赖的集合，D的闭包\(D^+\)是由D逻辑蕴涵的所有函数依赖和多值依赖的集合。

范式

第一范式（1NF）

如果关系R的所有域都是原子的，则称其属于第一范式。

例如 \(r(dept\_name, location, phone)\) 这个关系模式，如果我们规定phone是系公用电话（只能有一个），它就属于第一范式；如果phone中保存了系内所有老师的电话，这个属性的域就不是原子的（因为可以继续拆分为单个老师的电话），就不属于第一范式。

第二范式（2NF）

第二范式要求数据库表中的每个元组必须可以被唯一地区分，且主属性只依赖于主码，而不能依赖于主码的一部分。

例如\(r(ID,name,course,credit)\)不属于第二范式，因为\(ID，course\rightarrow name,credit\)，主码为\((ID,course)\)，但又存在\(ID\rightarrow name,course\rightarrow credit\).

第二范式只有历史意义，一般题目中不作考虑。

第三范式（3NF）

在2NF的基础上，消除了非主属性对码的传递函数依赖。准确条件是：

对于\(F^+\)中所有形如\(\alpha\rightarrow\beta\)的函数依赖，以下至少一项成立：

\(\alpha\rightarrow\beta\)是平凡的函数依赖；\(\alpha\)是R的一个超码；\(\beta-\alpha\)中的每个属性A都包含于R的一个候选码中。

注意\(\beta-\alpha\)中的每个属性A可以分别属于不同的候选码，只要它是候选码的一部分即可。

在工程上，一般认为满足第三范式的数据库设计就已经足够好了。

巴德范式（BCNF）

在3NF的基础上，消除了主属性对码的部分函数依赖和传递依赖。准确条件是：

对于\(F^+\)中所有形如\(\alpha\rightarrow\beta\)的函数依赖，以下至少一项成立：

\(\alpha\rightarrow\beta\)是平凡的函数依赖；\(\alpha\)是R的一个超码。

用函数依赖进行数据库设计的目标是：BCNF、无损、保持依赖。有时候无法达到所有目标，必须在BCNF和3NF中权衡。

第四范式（4NF）

在BCNF的基础上，消除了上述范式没能解决的冗余现象。准确条件是：

对于\(D^+\)中所有形如\(\alpha\rightarrow\rightarrow\beta\)的多值依赖，以下至少一项成立：

\(\alpha\rightarrow\rightarrow\beta\)是一个平凡的多值依赖；\(\alpha\)是R的一个超码。

分解

分解是为了使我们设计的模式符合要求的范式，分解方式是本节的重点。

• 有损分解

  对于分解后的两个模式进行自然连接后，无法完整地得到原有的信息。

  例如表 \(student(ID, name, dname)\)，如果分解为\(stu1(ID, name)\) 和 \(stu2(name, dname)\)，一旦出现重名而不同专业的学生，如\((01, Ming, CS)\) 和 \((02, Ming, SE)\)，将其分解为stu1和stu2再自然连接后会出现对应的四行：

  \((01, Ming, CS)\)、\((01, Ming, SE)\)、\((02, Ming, CS)\)、\((02, Ming, SE)\)，此时就无法区分01和02所属的专业了。

  有损分解是有害的，应当避免这样的分解。

• 无损分解

  对于分解后的两个模式进行自然连接后，能够完整地得到原有的信息。

  无损分解是我们希望进行的分解。在下文将介绍几种分解算法，它们都能求出无损分解。

若\(R_1,R_2\)是\(R\)的无损分解，则 \(r(R)\)上的函数依赖集闭包\(F^+\)中至少存在以下依赖中的一个：

​ \(R_1\cap R_2\rightarrow R_1\) ； \(R_1\cap R_2\rightarrow R_2\) 即\(R_1\cap R_2\)是\(R_1\)或\(R_2\)的超码。

3NF分解

求出F的正则覆盖\(F_c\)
对于\(F_c\)中的每一条函数依赖\(\alpha\rightarrow\beta\)，令\(R_i=\alpha\beta\)
如果所有\(R_i\)中都不包含R的候选码，就令\(R_{i+1}\)=候选码
遍历所有\(R_i\)，如果发现\(R_j\)包含于另一个模式\(R_k\)中，就将\(R_j\)删去

得到新的模式集（\(R_1, R_2, ..., R_n\)），且每个模式都符合3NF

BCNF分解

检查F中的每条函数依赖是否符合BCNF的要求（\(F_c\)更好用）
对不符合要求的函数依赖\(\alpha\rightarrow\beta\)，借助这条依赖将R分解为以下两个：
（\(R_i-\beta\)），（\(\alpha ,\ \beta\)）

4NF分解（与BCNF类似）

4NF分解

检查F中的每条函数依赖是否符合4NF的要求（\(F_c\)更好用）
对不符合要求的函数依赖\(\alpha\rightarrow\rightarrow\beta\)，借助这条依赖将R分解为以下两个：
（\(R_i-\beta\)），（\(\alpha ,\ \beta\)）