CS149ass4+extra

CS149并行系统 ass4 并行图算法+block gemm

pagerank

我研一的时候，实验室还经常提到这个算法，当时我刚开始学cs还很差，虽然现在也很菜（笑），但至少现在能直接手写出来，当然还是多线程版本。

void pageRank(Graph g, double *solution, double damping, double convergence) {

  // initialize vertex weights to uniform probability. Double
  // precision scores are used to avoid underflow for large graphs

  int numNodes = num_nodes(g);
  double init_prob = (double)1 / numNodes;
  bool converged = false;
  double *old_scores_matrix = (double *)aligned_alloc(64, numNodes * 8);
  double *new_scores_matrix = solution;
  int *out_size = (int *)aligned_alloc(64, numNodes * 4);
  int *zero_v = (int *)aligned_alloc(64, numNodes * 4);
  int zero_sz = 0;


#pragma omp parallel for
  for (int i = 0; i < numNodes; i++) {
    new_scores_matrix[i] = init_prob;
    old_scores_matrix[i] = init_prob;
    out_size[i] = outgoing_size(g, i);
#pragma omp critical
    {
      if (out_size[i] == 0) {
        zero_v[zero_sz++] = i;
      }
    }
  }

  while (!converged) {
    double global_diff = 0;
    double zero_score = 0;
#pragma omp parallel for reduction(+ : zero_score)
    for (int j = 0; j < zero_sz; j++) {
      zero_score += damping * old_scores_matrix[zero_v[j]] / numNodes;
    }
    double add_v = ((double)1.0 - damping) / numNodes + zero_score;
#pragma omp parallel for reduction(+ : global_diff) schedule(guided)
    for (int i = 0; i < numNodes; i++) {
      double &new_score = new_scores_matrix[i];
      new_score = 0;
      const int& is = incoming_size(g, i);
      Vertex *ib = (int *)incoming_begin(g, i);
      for (int j = 0; j < is; j++) {
        const Vertex& vj = ib[j];
        const int& sz_j = out_size[vj];
        new_score += old_scores_matrix[vj] / sz_j;
      }
    }
#pragma omp parallel for simd reduction(+ : global_diff)
    for (int i=0; i< numNodes; i++){
      double &new_score = new_scores_matrix[i];
      new_score = new_scores_matrix[i] * damping + add_v;
      global_diff += fabs(new_score - old_scores_matrix[i]);
      old_scores_matrix[i] = new_score;
    }
    converged = (global_diff < convergence);
  }
  free(old_scores_matrix);
  free(out_size);
  free(zero_v);
}

完全就是实现公式，但是需要注意的，每次把那么出度为0的节点单独计算一下。我第一次写的时候，把这些出度为0的节点当做每个点的邻居，导致算法奇慢无比。。。

BFS

top_down

void top_down_step(
    Graph g,
    vertex_set* frontier,
    vertex_set* new_frontier,
    int* distances)
{
#pragma omp parallel for schedule(auto)
    for (int i=0; i<frontier->count; i++) {

        int node = frontier->vertices[i];

        int start_edge = g->outgoing_starts[node];
        int end_edge = (node == g->num_nodes - 1)
                           ? g->num_edges
                           : g->outgoing_starts[node + 1];

        // attempt to add all neighbors to the new frontier
        for (int neighbor=start_edge; neighbor<end_edge; neighbor++) {
            int outgoing = g->outgoing_edges[neighbor];
            if(__sync_bool_compare_and_swap(&distances[outgoing], NOT_VISITED_MARKER, distances[node]+1)){
                int index = __sync_fetch_and_add(&new_frontier->count, 1);
                new_frontier->vertices[index] = outgoing;
            }
            // if (distances[outgoing] == NOT_VISITED_MARKER) {
            //     distances[outgoing] = distances[node] + 1;
            //     int index = new_frontier->count++;
            //     new_frontier->vertices[index] = outgoing;
            // }
        }
    }
}

算法流程：

• 将root node加入到frontier中
• while(frontier不为空):
  • 遍历frontier中所有点v
  • 遍历点v的所有邻居u，如果u没有被遍历过（也就是bfs访问），加入到new_frontier中，并且distances[u] = distances[v] +1
  • 遍历frontier后，交换frontier于new_frontier

boom_up

void bottom_up_step(Graph g,vertex_set* frontier, vertex_set* new_frontier, int* distances){

    int num_nodes = g->num_nodes;
    int round = distances[frontier->vertices[0]];
#pragma omp parallel for schedule(guided) 
    for(int node=0; node< num_nodes; node++){
        if(distances[node] == NOT_VISITED_MARKER){
            int start = g->incoming_starts[node];
            int end  = node == num_nodes-1? g->num_nodes: g->incoming_starts[node+1];
            for(int i= start; i< end; i++){
                int in_coming = g->incoming_edges[i];
                if(distances[in_coming] == round){ // 说明 in_coming 是当前frontier中点
                    distances[node] = distances[in_coming] + 1;
                    int index = __sync_fetch_and_add(&new_frontier->count, 1);
                    new_frontier->vertices[index] = node;
                    break;
                }
            }
        }
    }
}

boom_up和top_down有点相反的味道，类似于从叶子结点跑到根节点。

算法有些类似，唯一需要注意判断in_coming 是否在frontier中，这里其实有个隐含条件distances[in_coming] == round，如果in_coming的distance为当前round，那么一定在frontier中。

这个lab让我最大的收获，就是知道了gcc中atomic内建函数： https://gcc.gnu.org/onlinedocs/gcc-4.1.2/gcc/Atomic-Builtins.html

BLOCK GEMM

之前在课上其实也提供这个tiling操作，包括在公司实习时候也有大佬分享过GPU tiling操作：

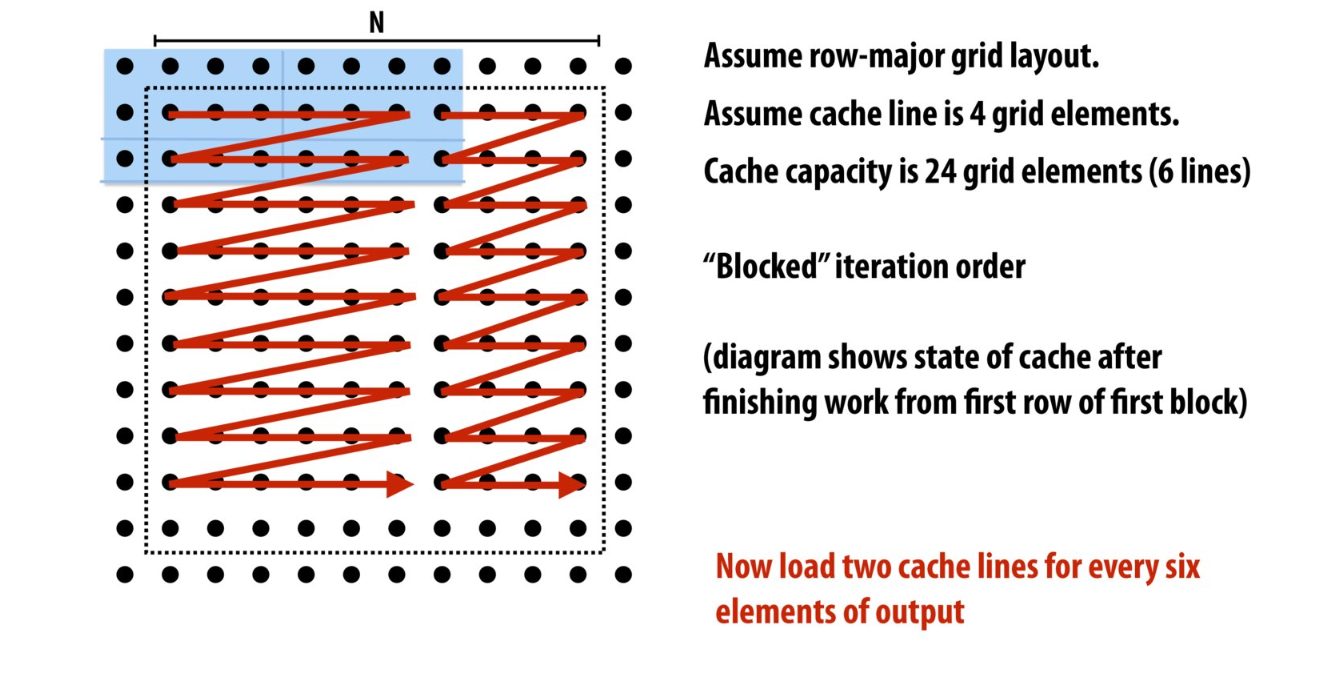
照着https://csapp.cs.cmu.edu/public/waside/waside-blocking.pdf，一顿实现就完事了：

export void gemm_ispc(uniform int m, uniform int n, uniform int k,
	 uniform double A[], uniform double B[], uniform double C[], uniform double alpha, uniform double beta) {
	// YOUR IMPLEMENTATION HERE
	uniform int blk_size = 1024;
	uniform int row_blk_nums = k / blk_size;
	uniform int col_blk_nums = n / blk_size;
	foreach(kk = 0 ... row_blk_nums){
		for(int jj = 0; jj < col_blk_nums; jj++){
			for(int i = 0; i < k; i++){
				int col_start = jj * blk_size;
				for(int j = col_start; j < col_start + blk_size; j++){
					int sum = 0;
					int k_start = kk * blk_size;
					for(int k_ = k_start; k_ < k_start + blk_size; k_++){
						sum += A[i*k + k_]* B[k_*n + j];
					}
					atomic_add_local(&C[i+n + j], sum);
				}
			}
		}
	}
}