多头Attention 和 自注意力机制
这个多头attention确实挺搞的,这个东西绕来绕去,看torch的文档也看不懂,看源码也迷迷糊糊的,可能我的智商就是不够吧。。。枯了
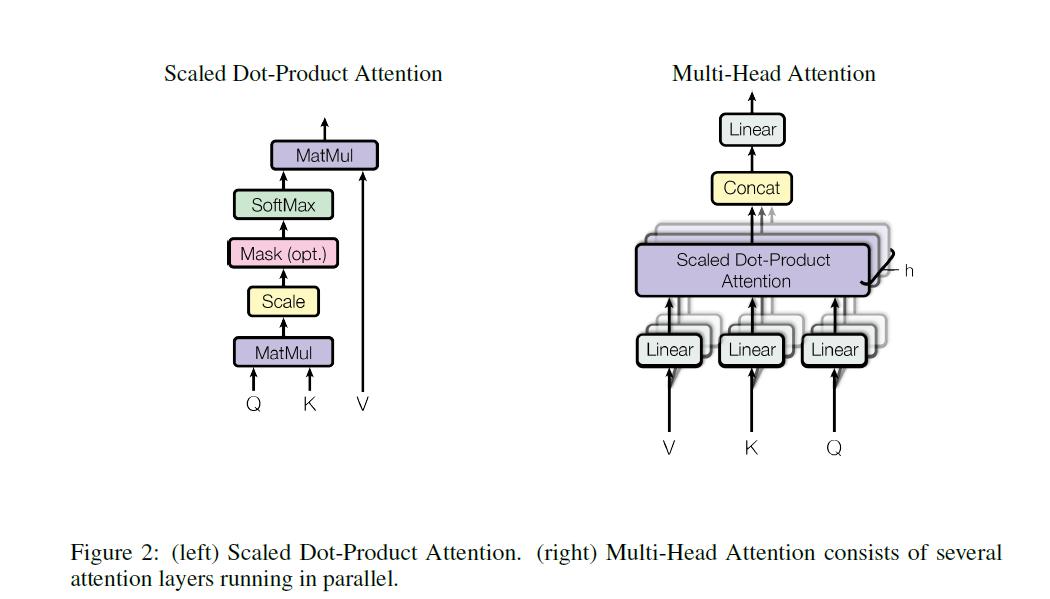
论文里的公式求法,可以看到它因为是self-multiheadsAttention。多头自注意力机制,所以它这里的Q K V 实际上是同一个东西,也就是最后一维都是相同的。
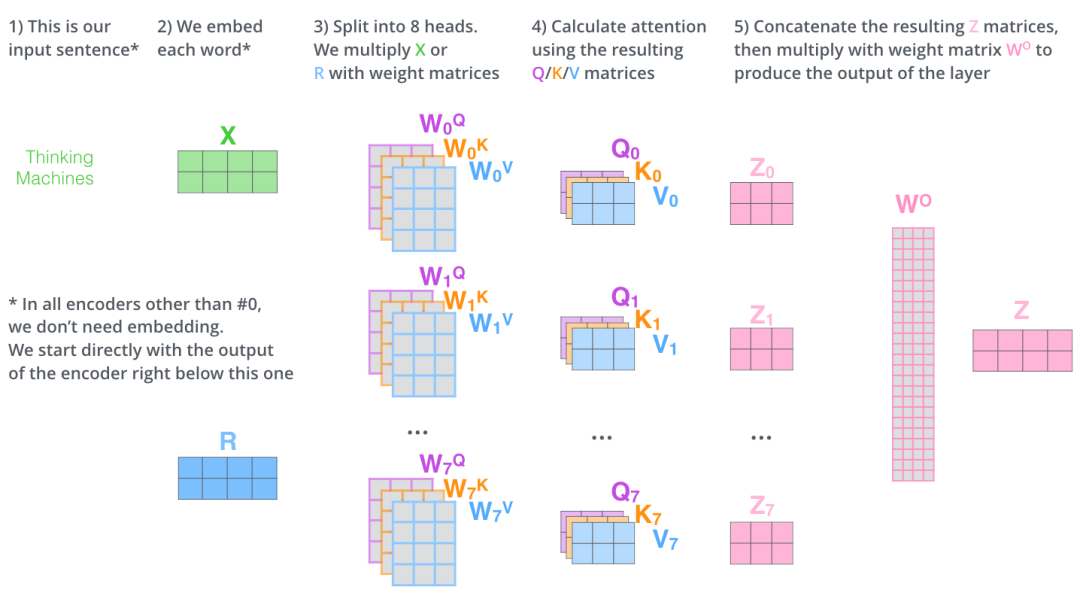
为什么这里可以直接concat起来,是因为它将Q、K、V最后一维都进行了切割,也就是说,它的多头attention不是说使用多个attention weight,而是说对不同part部分进行attention。比如论文将Q、K、V最后一个维度切成了8块,它的8头attention,就是每个attention就对这一块部分进行attention机制,最后进行concat。这也是一个有意思的点,这样就直接用点积attention来一次矩阵乘法就行了。

这里有个参考的回答:
这里有两张参考的图片:
torch 文档
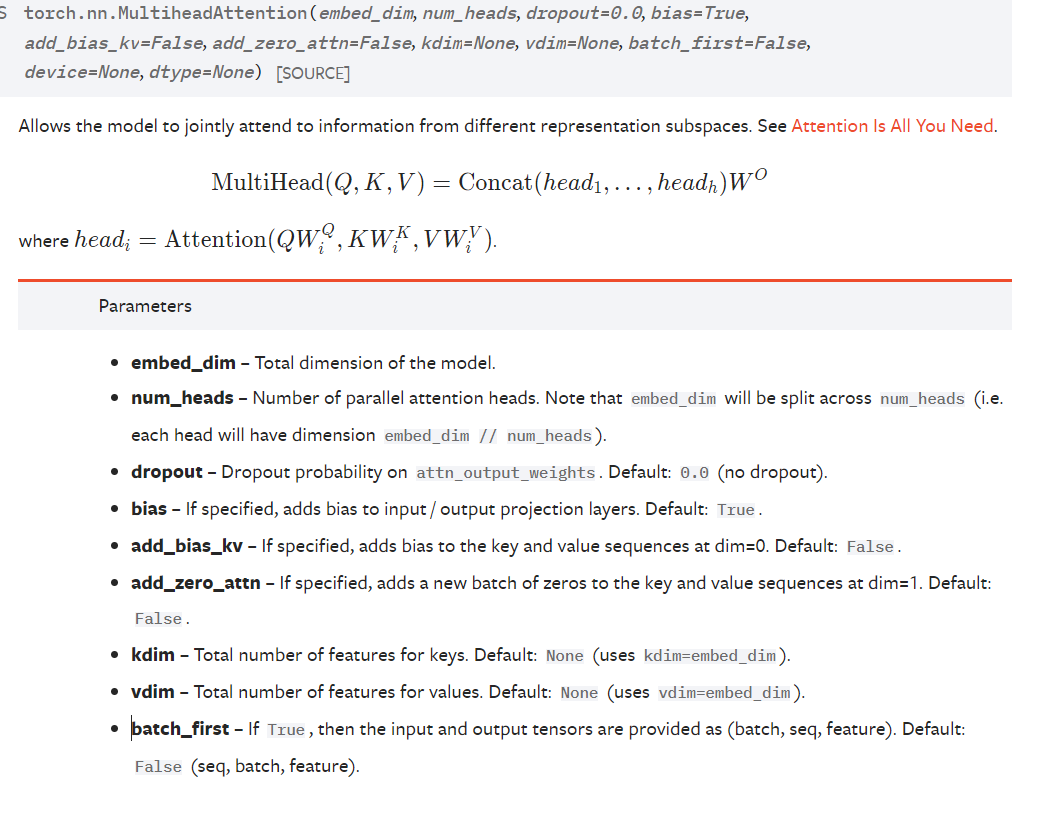
这里的embed_dim 就是后面Q的dim(最后一维)也就是词向量的维度,这是模型输出的维度,默认q、k、v的最后维度一致。
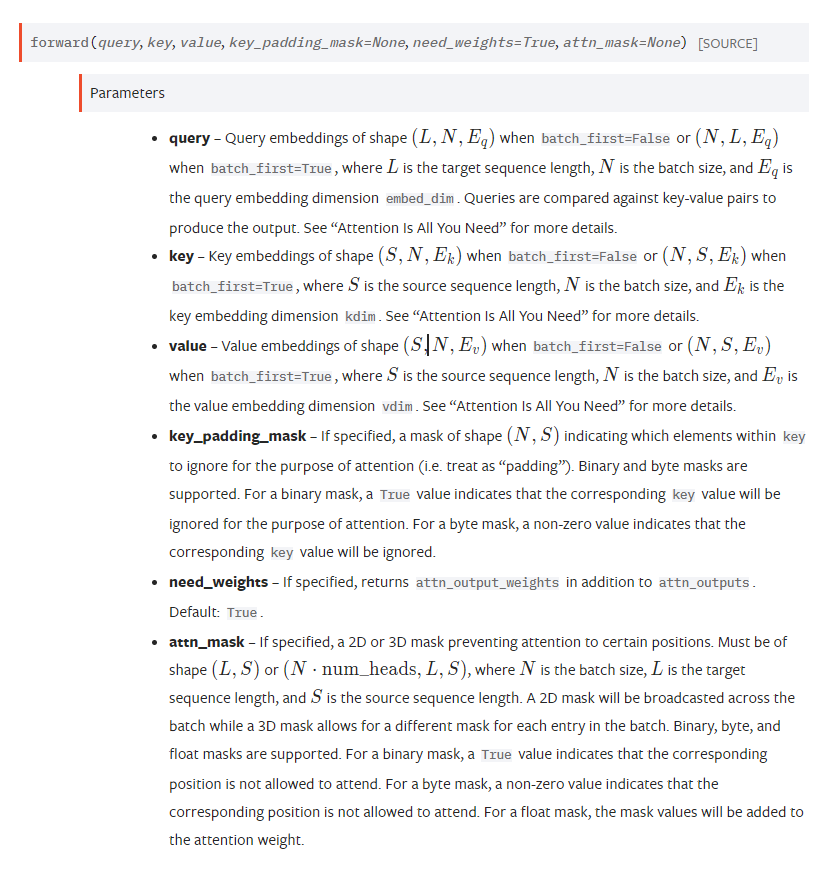
key_padding_mask 是padding mask 是掩key的
attn_mask 是掩key_value pair的。
这么说可能很难理解,key_padding_mask就是说句子序列中有多少个padding,这些padding是不要的。但是attn_mask 是用来说,我不能提前看到后面的词。(这个还是在自注意力机制用到),因为transformer的decoder第一层的自注意力层不能看到未来的词。
自己实现多头注意力机制
import torch
import torch.nn as nn
import math
from d2l import torch as d2l
class MultiAttention(nn.Module):
def __init__(self, embed_dim, num_heads, qdim=None, kdim=None, vdim=None, hdim=256, dropout=0.0) -> None:
super(MultiAttention, self).__init__()
self.attention = d2l.DotProductAttention(dropout)
self.num_heads = num_heads
nn.MultiheadAttention()
# 先做一个全连接层好把Q、K、V不同维度转为同一维度
self.W_q = nn.Linear(qdim, embed_dim)
self.W_k = nn.Linear(kdim, embed_dim)
self.W_v = nn.Linear(vdim, embed_dim)
self.W_o = nn.Linear(embed_dim, emded_dim)
def forward(self, Q, K, V):
# 注意这里的Q 的shape (batchsize, qn, qdim)
# K (batchsize, kvn, kdim)
# V (batchsize, kvn, vdim)
Q = self.trans(self.W_q(Q), self.num_heads)
K = self.trans(self.W_k(K), self.num_heads)
V = self.trans(self.W_v(V), self.num_heads)
# Q (batchsize *numheads, qn, embed_dim/num_heads)
output = self.attention(Q, K, V)
# output shape (batchsize*num_heads, qn, kvn, embed/num_heads)
# 这里没有返回attentionweight,但attentionweight的shape (batchsize*num_heads, qn, kvn)
# output最后一维的embed/num_heads,是因为我们将V的最后一维切割了。
output = self.retrans(output, self.num_heads)
return self.W_o(output)
def trans(self, X, num_heads):
# X shape (batchsize, 查询或者‘键值对’数, embed_dim)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
X = X.permute(0, 2, 1, 3)
X = X.reshape(-1, X.shape[2], X.shape[3])
return X
def retrans(self, X, num_heads):
# X shape (batchsize*num_heads, 查询或者‘键值对’数, embed_dim/num_heads)
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
X = X.permute(0, 2, 1, 3)
X = X.reshape(X.shape[0], X.shape[1], -1)
return X
attention = MultiAttention(256, 2, 64, 64, 64)
q= k= v= torch.ones((32, 35, 64))
s = attention(q, k, v)
这里我其实写的很不标准,因为几个全连接搞得挺混乱的。但其实思想也是一致的。
自注意力机制
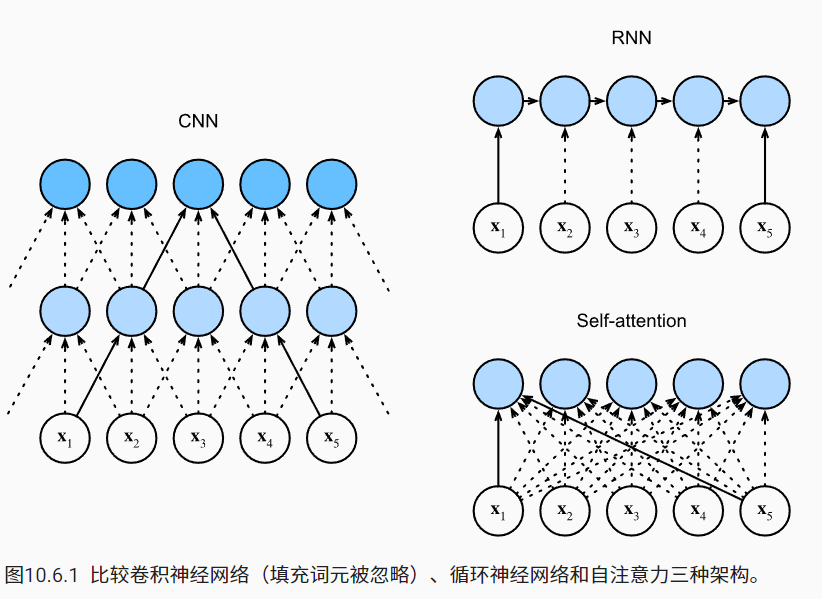
可以看到RNN是很有时序性的,它是要求一个一个输入。CNN也可以保留一定的时序性,因为卷积核的感受野可以保留部分时序信息。但是self-attention机制是完全没有时序性的,它一次就可以看完全部。
位置编码
这里就引入了位置编码这个概念:
X = X + P其中P就是位置编码,对应的值:

