cs224w学习笔记（02）传统图机器学习方法

传统图机器学习方法

传统机器学习的任务级别可以划分为三个级别：Node-level、Edge-level、Graph-level
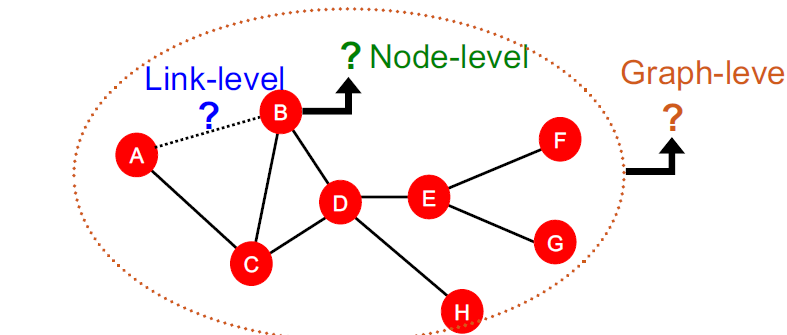
20210912145612

按照节点的不同，特征也分别为nodes、links、graphs

传统的机器学习模型

  • random forest
  • SVM
  • Neural network, etc

$ x \rightarrow y $

想得到好的训练效果关键在于使用有效的特征，而传统的机器学习方法使用人工设计特征。以下以无向图为例：

Node-leverl Tasks

描述节点重要性的方法

Eigenvector centrality

model the centrality of node 𝑣 as the sum of the centrality of neighboring nodes

\[c_v = \frac{1}{\lambda} \sum\limits_{u\in N(v)} c_u \]

其中\(\lambda\) 为一个正常数

这个递归式子可以写为：

\[\lambda c = Ac \]

其中A为邻接矩阵，c就是该矩阵A的特征向量，其中\(\lambda\)为特征值

很好理解，A矩阵的每一行i非0值，表示与i节点相邻的节点，与c相乘后得到就是\(\sum\limits_{u\in N(v)}c_{u}\)

Betweenness centrality

A node is important if it lies on many shortest paths between other nodes.

\[c_v = \sum_{s\ne v \ne t}\frac{\text{s与t之间包含v的最短路径数}}{\text{s与t的最短路径数}} \]

人话就是两个点s与t之间有n条最短路径，其中k条过v点，那么k/n就是s与t两个点贡献的值，s与t是图上任意过v的点，所以把排列组合一下，得到所有的和，即Betweenness centrality。

Closeness centrality

A node is important if it has small shortest path lengths to all other nodes

\[c_v= \frac{1}{\sum_{u\neq v}\text{u和v两个点的最短路径长度}} \]

简单来说，就是某个点到其他点距离越近越重要。

Clustering Coefficient

Measures how connected 𝑣"𝑠 neighboring nodes are

该系数用于判断v的相邻节点之间的连接程度，这个可以用于推荐算法。

\[e_v = \frac{\text{相邻节点之间的边数}}{C_{k_v}^{2}} \]

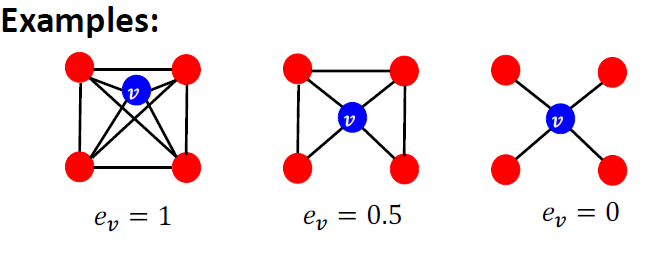
20210912153606

Clustering Coefficient可以看做在算三角形数

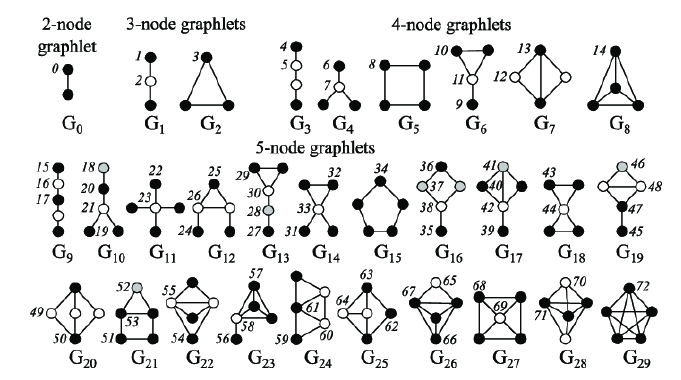
Graphlets

Graphlets : Rooted connected non-isomorphic subgraphs

Graphlet Degree Vector (GDV) counts #(graphlets) that a node touches

Graphlets 是一些非同构子图，可以看为一些特定的形状图

20210912154148

GDV计算一个结点可以touch多少graphlets数，用于对节点的local network topology进行描述。

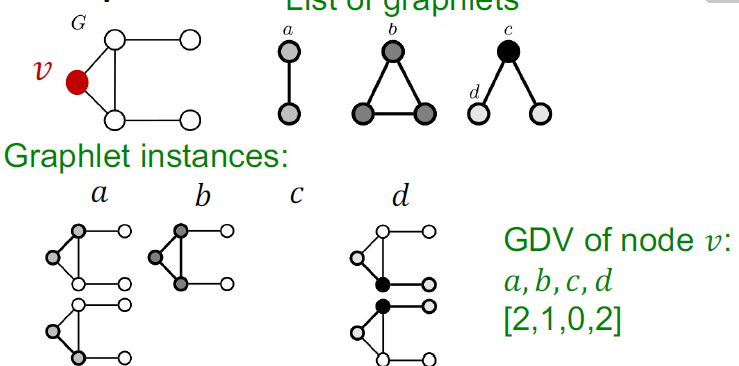
20210912155122

这里解释一下，为什么c是0，因为看graphlets数，可以把其他所有无关节点全部节点抹掉，把c套到v点后，只有一个包含三个节点的子图，且这个子图唯一（也就是b只有一种情况），就是一个三角形，那么就不存在c这种情况，所以c为0.

关于节点特征获取方法可以分为：

节点特征的获取方法：
importance-based features：

Node degree

Differnet node centrality measures

structure-based features：

Node degree

clustering coeefficient

Graphlets count vector

对link也就是edge进行预测，是edges-level任务，关键在于设计两个节点之间的特征。

Remove a random set of links and then aim to predict them

就是随机移除一些边，然后进行预测。

给出\(G[t_0,t_{0}^{'}]\)即处于\(t_0,t_{0}^{'}\)之间的图G，预测图\(G[t_1,t_{1}^{'}]\)即处于\(t_0,t_{0}^{'}\)的图G

评价预测的好坏就是看预测新出现的edges n是否在\(t_0,t_{0}^{'}\)出现

methodology：

  1. 选择一对节点（x，y），计算score c(x,y)

  2. 根据c(x,y)对节点对进行排序

  3. 将top n个节点对作为预测值

  4. 和实际的\(G[t_1, t_{1}^\prime]\)做对比

计算score的方法

Distance-Based Features

Shortest-path distance between two nodes

计算两个节点的之间的最短路径长度作为节点对的score

缺点：不能体现节点之间度的相似程度

Local Neighborhood Overlap

  • common neighbors

    \[|N(v_1)\cap N(v_2)| \]

    计算v1与v2之间的相同邻居节点数目

  • Jaccard's coefficient

    \(\frac{|N(v_1)\cap N(v_2)|}{|N(v_1)\cup N(v_2)|}\)

    交集邻居节点数除以并集邻居节点数

  • Adamic-Adar index

    \(\sum_{u \in N(v_1)\cap N(v_2)}\frac{1}{\log(k_u)}\)

    先得到v1和v2的共有邻居节点，再对这些邻居节点的度做log运算后求和

局限性：

​ 如果节点对(v1,v2)没有邻居节点，那么Local Neighborhood Overlap方法得到的score值为0，然而这两个节点对还是有可能相连的。

Global neighborhood overlap
矩阵乘法

矩阵乘法的定义：

\[C = A \times B\\ C_{ij} = \sum_{k=1}^{n}A_{ik} \times B_{kj}\\ A^2 = A \times A\\ A_{ij}^2= \sum_{k=1}^{n}A_{ik} \times A_{kj}\\ \]

而邻接矩阵用0,1表示两个节点是否关联，那么矩阵乘法A x A 中Aij实际是找有多少个节点k满足，由i到k到j成立。那么A^2实际上算的是i，j两个节点之间路径长度为2的路径数，也就是k点数。

那么矩阵的n次幂求得的矩阵中\(A_{ij}^n\) 就是节点对（i，j）之间路径长度为n的路径数。

katz index

Katz index: count the number of paths of all lengths between a given pair of nodes.

很难直接下个清晰的中文文字定义，这里使用原文的定义。

\[S_{v_1,v_2} = \sum_{l = 1}^{\infty} \beta^l A_{v_1,v_2}^l\\ S = \sum_{i = 1}^{\infty}\beta^i A^i = (I - \beta A)^{-1} - I\\ \text{prove: }\\ (I- \beta A)(I+S)\\ =(I- \beta A)(I + \beta A+\beta^2A^2+...)\\ =(I + \beta A+\beta^2A^2+...)- (\beta A+\beta^2A^2+...)=I\\ \\ then: I+S = (I-\beta A)^{-1} \\ \\ so: S = (I - \beta A)^{-1} - I \]

image-20210922202812509

Graph-Level Features and Graph Kernels

Graph-Level Features

SVM

超平面：

\[X^TW + b = 0\\ margin = \frac{2}{||w||} \]

img

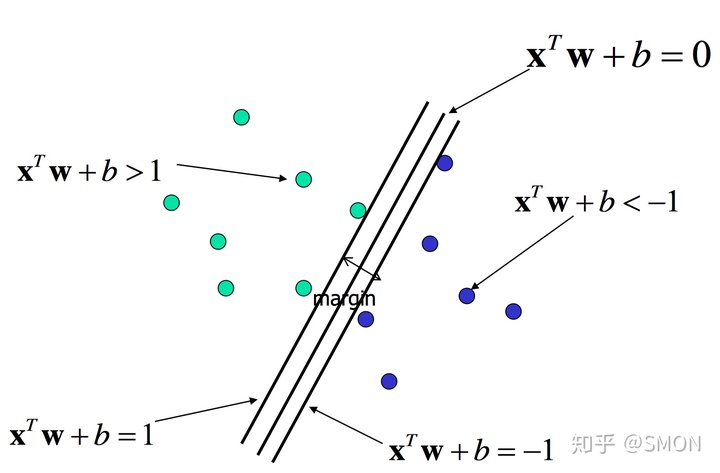
支持向量

训练集的样本点中与分离超平面距离最近的样本实例点称为支持向量。

  • 正实例点位于超平面H1：\(y_i(w^Tx+b)=1\)
  • 负实例点位于超平面H2： \(y_i(w^Tx+b)=-1\)

H1与H2之间的距离就是上面提到的margin，margin越大，分离的可信度越高。

distance = \(\frac{2}{||w||^2}\)

  • 决定分离超平面只有支持向量发挥作用，其他实例不起作用
  • 移动支持向量会改变分离超平面
求解约束最优化：

\[\min_{w,b} \frac{1}{2} \parallel{w}\parallel ^2\\ s.t \quad y_i(w\cdot x_i +b) -1 \geq 0, \quad i=1,2,\cdots,N \]

若数据集T线性可分，这将所有样本点完全正确分开的最大间隔分离的超平面存在且唯一。

拉格朗日对偶法

拉格朗日函数：

\[L(w,b,\alpha) = \frac{1}{2} \parallel w\parallel^2 - \sum_{i=i}^N \alpha_i y_i (w\cdot x_i+b)+\sum_{i=1}^N \alpha_i \]

根据拉格朗日对偶性，原问题的解可以变为对偶问题，即极大极小问题：

\[\max_\alpha \min_{w,b} L(w,b,\alpha) \]

求\(\min_{w,b} L(w,b,\alpha)\):

\[\triangledown_w L(w,b,\alpha) = w-\sum_{i=i}^N \alpha_i y_i x_i = 0\\ \triangledown_b L(w,b,\alpha) = -\sum_{i=1}^N \alpha_iy_i = 0\\ so: \quad w= \sum_{i=1}^N \alpha_i y_i x_i\\ \sum_{i=1}^N\alpha_i y_i =0 \]

带入拉格朗日函数，得到：

\[\min_{w,b} L(w,b,\alpha) = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i\cdot x_j ) +\sum_{i=1}^N \alpha_i \]

再有约束：

\[\min_\alpha \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i\cdot x_j ) - \sum_{i=1}^N \alpha_i\\ s.t \quad \sum_{i=1}^N\alpha_i y_i =0\\ \alpha_i \ge 0 \quad i=1,2,\cdots,N \]

由该约束条件又可以得到最优化解 $ \alpha ^* = [\alpha_1*,\alpha_2,\dots,\alpha_N^]$

由KTT条件，可以得到原始最优化问题的解为：

\[w^* = \sum_{i=1}^N \alpha_i^* y_i x_i\\ b^* = y_j - \sum_{i=1}^N \alpha_i^* y_i (x_i \cdot x_j) \]

故分离超平面可以写为：

\[\sum_{i=1}^N \alpha_i^* y_i(x_i\cdot x ) + b^* = 0 \]

分离决策函数：

\[f(x) = sign(\sum_{i=1}^N \alpha_i^* y_i(x_i\cdot x ) + b^* ) \]

核函数

为什么我们需要核函数？

上面介绍的SVM，都是用于线性可分的情况下，但是，对于线性不可分的情况比如下图左边这种情况，就很难找到一个好的超平面将数据集分开。但是如果我们将数据点向高维空间做映射，那么原问题就变成了了一个线性可分问题，我们可以通过一个平面将数据集分开。

img

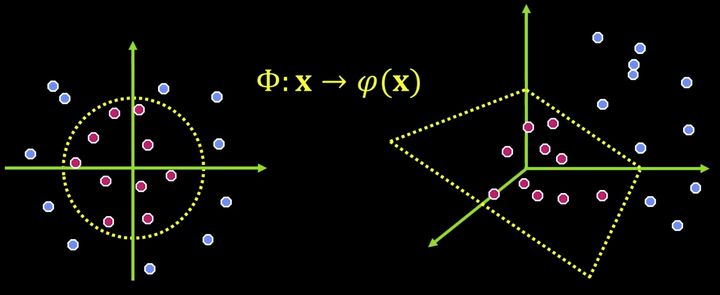
核函数的定义：

\[\text{设$X$为输入空间，$H$为特征空间，若存在一个映射关系:}\\ \phi (x): X \rightarrow H\\ \text{是的所有$x,z \in X$，函数K(x,z)满足条件}\\ K(x,z)= \phi(x)\cdot \phi(z)\\ \text{则称K(x,z)为核函数，$\phi(x)$为映射函数} \]

核技巧的思想就是，不显示的定义映射函数，而只定义核函数K(x,y)。

常用的核函数有线性核函数、多项式核函数、高斯核函数等。

举个例子：\(R^2 \rightarrow R^3\)

\[K(x,z) = (x\cdot z)^2\\ x = (x_1,x_2) , \quad z = (z_1,z_2)\\ (x\cdot z)^2 = (x_1z_1)^2 +2x_1z_1x_2z_2 +(x_2z_2)^2\\ 若映射为: \phi(x) =((x_1)^2,\sqrt{2} x_1 x_2 , (x_2)^2)\\ 很容易判断出K(x,z)= \phi(x)\cdot \phi(z)\\ \]

注意映射不唯一！

所有我们不必要显示的定义映射函数，只需要定义核函数。

SVM的核函数

\[f(x) = sign(\sum_{i=1}^N \alpha_i^* y_i(x_i\cdot x) + b^* )\\ = sign(\sum_{i=1}^N \alpha_i^* y_i(\phi(x_i)\cdot \phi(x) ) + b^* )\\ = sign(\sum_{i=1}^N \alpha_i^* y_i(K(x_i,x) + b^* ) \]

可以看到核方法能够处理线性不可分的问题。

核函数的要求

核矩阵的定义：每个点映射后的内积构成的矩阵，如果要成为核函数，那么核矩阵一定要是半正定的。

image-20210923110256421

一个大小为 $n\times n $的实对称矩阵 A ，若对于任意长度为n的非零向量X，有 $X^TAX≥0 $恒成立，则矩阵 A 是一个半正定矩阵。

Graph Kernel

img

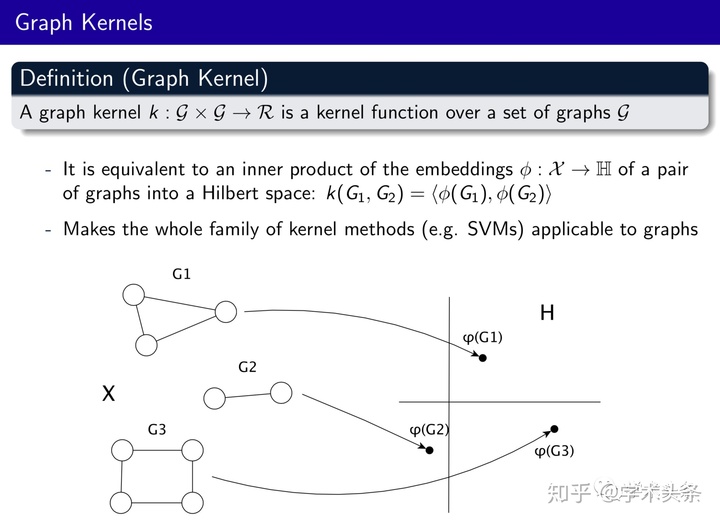
将整个图映射到希尔伯特空间，从而可以使用SVM对其进行分类。

graphlet kernel

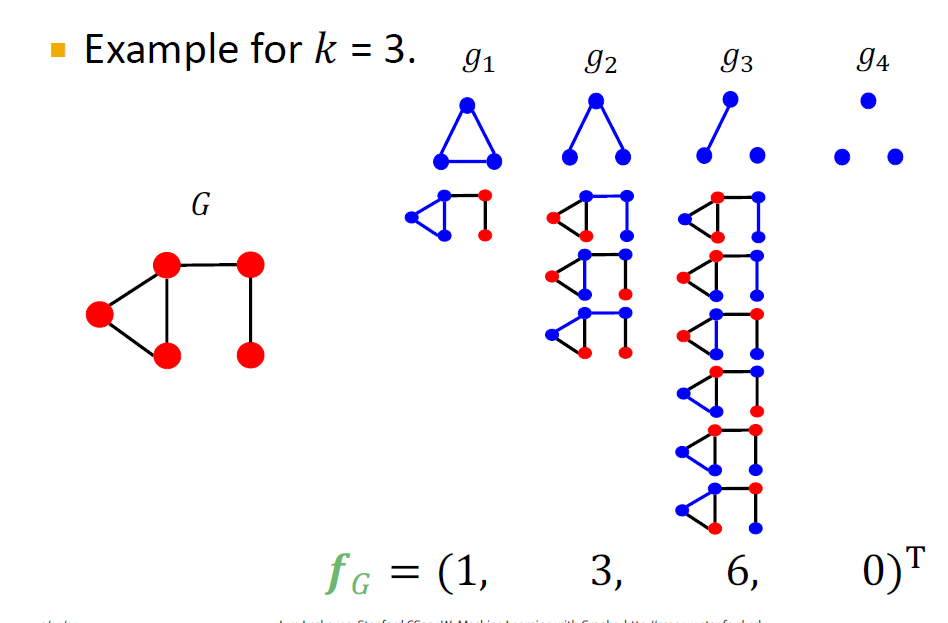
这里的graphlet与之前的graphlet有所区别，这里的graphlet可以有不相连的异构情况

比如：

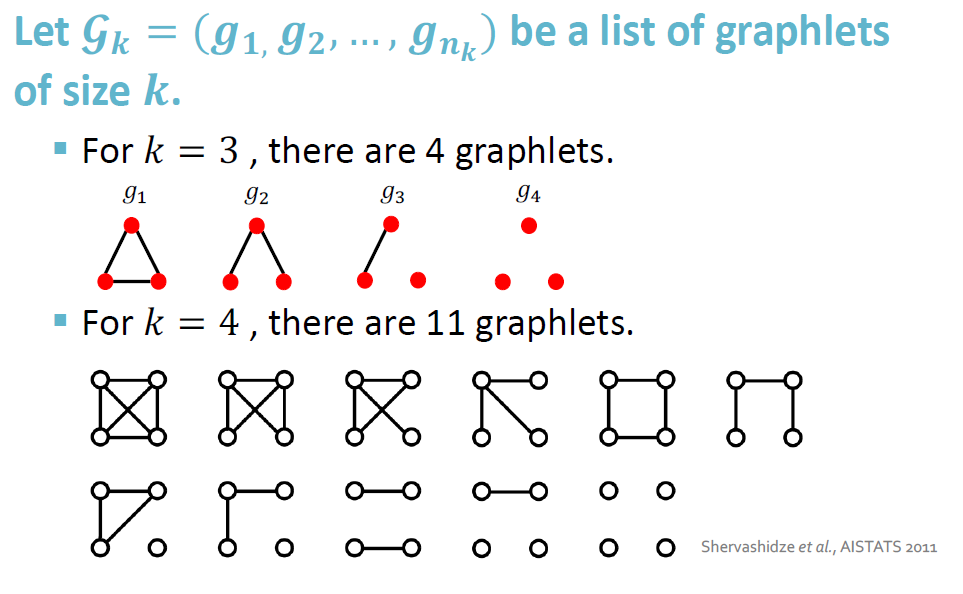
image-20210923114915038

原本k=3，只有两种情况，这里多了不相连的两种情况

映射关系可以写为：

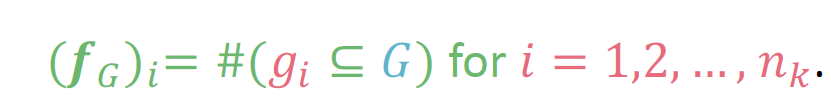
image-20210923115051437

统计子图\(g_i\)在图G中的出现次数，得到一个向量

image-20210923115204367

核函数的定义为：

\[K(G,G^\prime) = <\phi(G),\phi(G^\prime)> \]

归一化后：

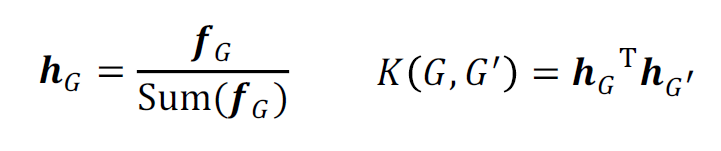
image-20210923115618617

graphlet kernel的limitations
  • 特征空间的维度随着子图结构的复杂会发生指数增长

Counting size-𝑘 graphlets for a graph with size 𝑛 by enumeration takes \(n^k\)

  • 在判断子图问题时，会遇到NP-hard

  • 计算向量时，复杂度很高

    If a graph’s node degree is bounded by 𝑑, an \(𝑂(𝑛𝑑^{k-1})\)algorithm exists to count all the graphlets of size 𝑘

WL(Weisfeiler-Lehamn) kernel

一个词：Color refinement

思路：

  • 给定两个图\(G,G^\prime\) ,对其做初始化init。

  • 根据哈希算法进行迭代

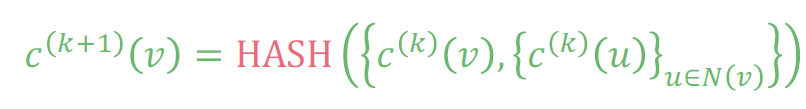
    image-20210923120614252

  • 迭代k步后，得到最后的矩阵

init：

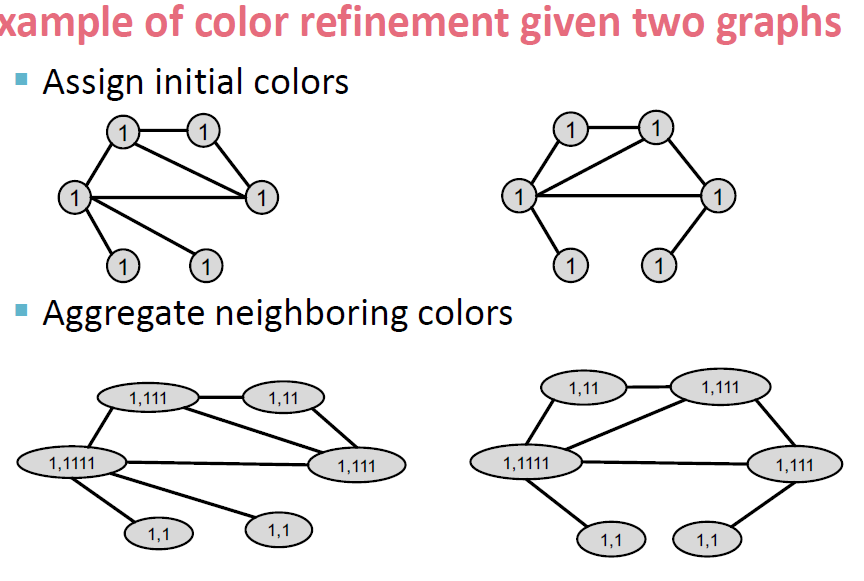
image-20210923120448457

Iteratively refine node clors

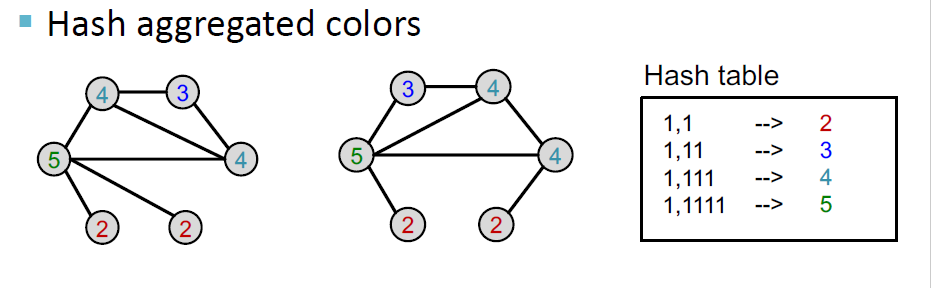
image-20210923120644702

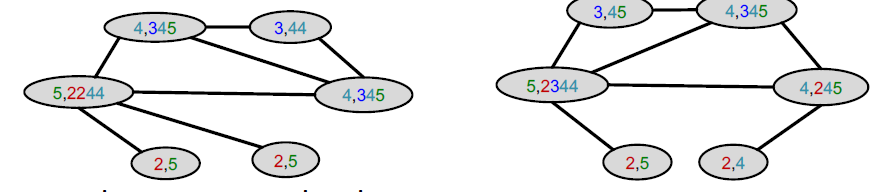
image-20210923120749767

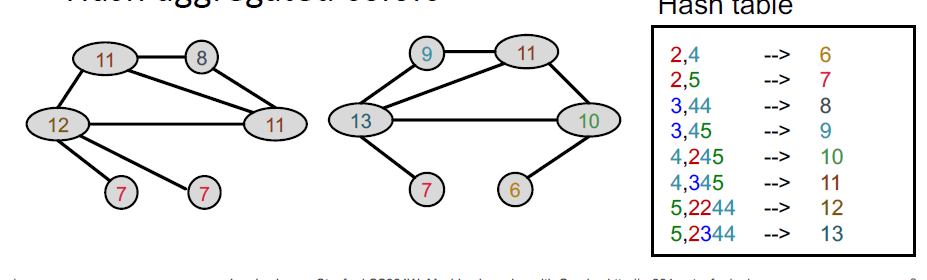
image-20210923120814042

计算得到特征矩阵

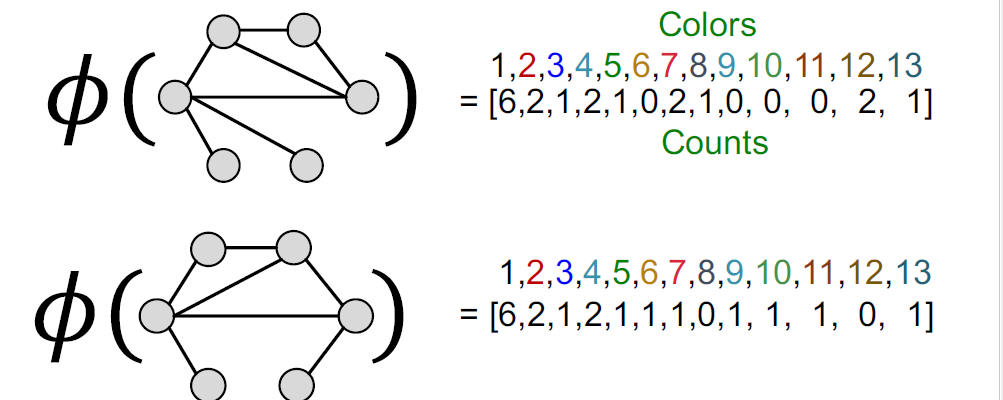
image-20210923120849078

核函数

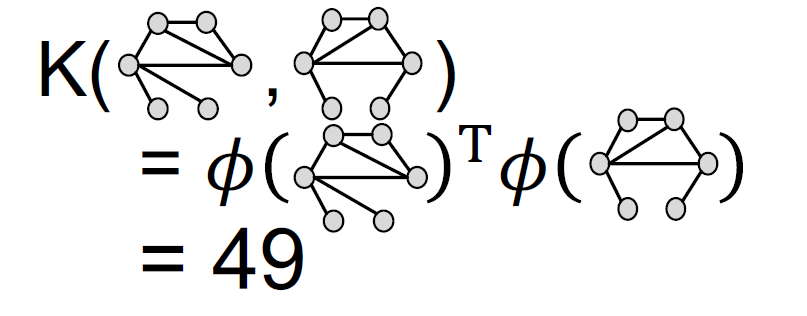
image-20210923120918448

\[k_{WL}(G, G^\prime) = <\phi(G),\phi(G^\prime)> \]

WL kernel的优点
  • WL kernel计算效率高，color refinement的每一步的复杂度是linear in #(edges)
  • 计算kenel value，只要要考虑两个图。
  • 计算颜色的复杂度linear in #(nodes)
  • 总的来说，复杂度是linear in #(edges)
Graphlet kernel 和 WL kernel的对比

image-20210923122544161

posted @ 2021-09-23 12:42  kalice  阅读(343)  评论(0)  编辑  收藏  举报