组合数学起步-排列计数[ZJOI2010][BZOJ2111]

<题面>

数据范围：$1 \leq N \leq 10^6, P \leq 10^9 $

这个题……

以为是排列，其实是组合

题目中说是从所有排列中找到Magic的，就是

$p_{i/2} \leq p_i$ 满足的情况

我拿着排列想了半天，发现

这个题和排列一点关系也没有

而且我打了几个表，看了下可行结果，也不能逆向求

后来是一个提示：用堆，dp

堆啊……

我扯了一会大根堆，发现堆的形态有不确定性，dp起来费力耗时

所以就是小根堆了：小根堆的形态不变，只要找填数的方案，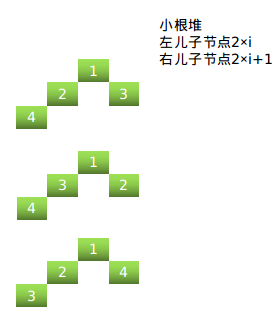

那么这里如何做呢？

对于每一个叶子节点和唯一值，只有一种方案

然后对于根节点，比根大的数作为叶节点，只要分成两部分就可以

但是如何分也不必要记录，只要记录方案数

由于是分步求解，

所以要把每个子树上的方法与本次分的方法相乘。

式子：$dp[i]=C_{siz[i]-1}^{siz[2*i]}*dp[i*2]*dp[i*2+1]$其中$siz[i]$是以$i$为根的树节点数

于是就可以得到结果$dp[1]$

当然要从$n$跑到$1$了

下面是另一部分

$C_n^m\%p$怎么求？

卢卡斯定理，p一定要是素数。

具体证明和代码见这里

蒟蒻不会了～～

 然后里面的细节就是，求阶乘及其逆元，可以打表，现求逆元也可以。

用 $a^{p-2}$ 的快速幂求逆元

#include <iostream>
#include <cstdio>
#include <algorithm>
#define N 2000100
#define LL long long
using namespace std;
LL p,n;
int siz[N];
LL fac[N],inv[N],dp[N];
LL ppow(LL a,LL b){
    LL k=1;
    while(b){
        if(b&1)k=k*a%p;
        a=a*a%p;
        b>>=1;
    }
    return k;
}
void prerun(){
    for (int i=n;i>=1;i--){
        siz[i]=siz[i*2]+siz[i*2+1]+1;
    }
    fac[0]=1;
    for (int i=1;i<=n;i++){
        fac[i]=fac[i-1]*i%p;
    }
}
LL C(LL m,LL n){
    if(n<m)return 0;
    return fac[n]*ppow(fac[m],p-2)%p*ppow(fac[n-m],p-2)%p;
}
LL lucas(LL m,LL n){
    if(m==0)return 1;
    return lucas(m/p,n/p)*C(m%p,n%p)%p;
}
int main (){
    scanf("%lld%lld",&n,&p);
    prerun();
    for (int i=n;i>=1;i--){
        dp[i]=lucas(siz[i*2],siz[i]-1);
        if(i*2<=n)dp[i]=dp[i]*dp[i*2]%p;
        if(i*2+1<=n)dp[i]=dp[i]*dp[i*2+1]%p;
    }
    printf("%lld\n",dp[1]);
    return 0;
}

真不知道没有题解怎么活～～

主要参考：Rorschach_XR的[ZJOI2010]排列计数 题解