[洛谷P4556][BZOJ3307]雨天的尾巴-T3订正
线段树合并+树上差分
题目链接（···） 「简单」「一般」——其实「一般」也只多一个离散化
考试时想法看>这里<
总思路：先存所有的操作，离散化，然后用树上差分解决修改，用权值线段树维护每个值的个数，最后dfs合并处理答案（先处理儿子，再合并自己和儿子，递归解决）
简单版当然不用离散话辣。
做了好几天，感觉自己傻了。
但是好像也不是这样的
事实上，这道题确实扩充了我对线段树的认识。
它它它还可以不存左右区间的啊？——一定是我太蒻了
先附样例以示敬意
20 50 8 6 10 6 18 6 20 10 7 20 2 18 19 8 1 6 14 20 16 10 13 19 3 14 17 18 11 19 4 11 15 14 5 18 9 10 12 15 11 14 87 12 1 87 14 3 84 17 2 36 6 5 93 17 6 87 10 14 93 5 16 78 6 15 93 15 5 16 11 8 50 17 19 50 5 4 87 15 20 78 1 17 50 20 13 87 7 15 22 16 11 94 19 8 87 18 3 93 13 13 87 2 1 87 2 6 22 5 20 84 10 12 93 18 12 87 16 10 93 8 17 93 14 7 36 7 4 22 5 9 87 13 10 16 20 11 50 9 16 84 10 17 16 19 6 87 12 2 36 20 9 94 9 2 84 14 1 94 5 5 94 8 17 16 12 8 36 20 17 78 12 18 50 16 8 94 2 19 36 10 18 36 14 19 50 4 12 50
87 36 84 22 87 87 22 50 84 87 50 36 87 93 36 94 16 87 50 50
我还是第一次见这么恐怖的样例
不过它也是我的救命稻草，让我骗了5分，这是之前的事
样例以1为根的巨树
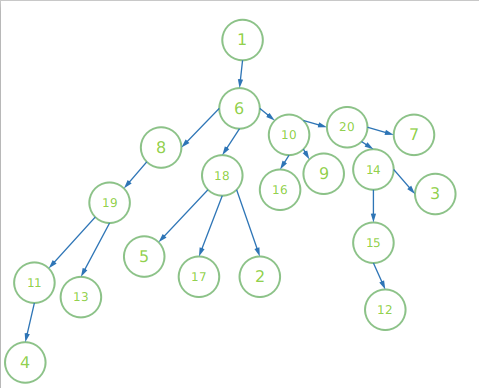
还是能看下的
树上差分就是通过修改树上某些节点的值来修改一段区间值的方法，比较常用
比如我们需要加树上一个区间
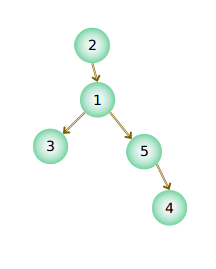想这样，加从3到4的区间，每个加1（加N也一样）
那么我们按照差分法，3++，4++，1--，2--
「公式」其实是 x+n ,y+n ,lca(x,y)-n ,father[lca(x,y)]-n
别告诉我你不会lca，虽然我也是刚学了实用的版本
结果是这样的
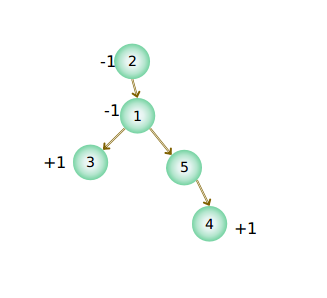这一步很快的···
我们要的结果当然不是±1什么的，要的是1或0
所以下面就是dfs统计结果（‘=’号前是过程，‘=’后是结果）
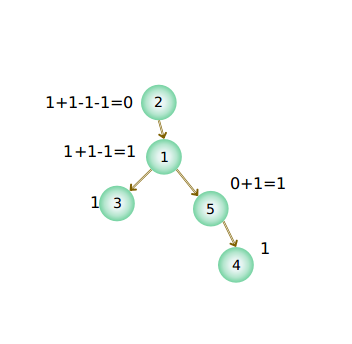仿佛得到了结果
这样我们就能够离线处理树上的区间加减
注意：只能是离线，N个修改，一次输出
线段树合并前面已经说过，这里不再细讲。
这个题仿佛对内存的限制很苛刻（我MLE 22 次，数过，想哭），所以线段树的节点一定要节约开空，只开最大值和左右儿子指针
//鬼知道我调了几天的是这个傻点
左右区间可以递归维护，不必要一定存在节点里，
也不必须在维护最大值时捆绑维护下标，查询时的O（NlogN）还是可以接受的
1 #include <algorithm> 2 #include <iostream> 3 #include <cstring> 4 #include <cstdlib> 5 #include <cstdio> 6 #include <cmath> 7 #include <queue> 8 #define N 200001 9 #define B 2*N 10 #define logN 31 11 using namespace std; 12 struct ST{ 13 int f,t,next; 14 };ST rs[B]; 15 int tot=0,fl[N],n,m,len; 16 void add(int f,int t){ 17 rs[tot].f=f; 18 rs[tot].t=t; 19 rs[tot].next=fl[f]; 20 fl[f]=tot; 21 tot++; 22 } 23 struct XDS{ 24 XDS *lid,*rid; 25 int maxn; 26 XDS(){ 27 lid=rid=NULL; 28 maxn=0; 29 } 30 };XDS *root[N]; 31 struct CON{ 32 int x,y,z; 33 };CON q[N]; 34 int val[N]; 35 int fvind(int i){ 36 return lower_bound(val,val+len,i)-val+1; 37 } 38 inline void build(XDS *&n){ 39 n=new XDS(); 40 } 41 void add(XDS *&rt,int v,int k,int l,int r){ 42 if(rt==NULL)build(rt); 43 if(l==r){ 44 rt->maxn+=k; 45 return ; 46 } 47 int mid=(l+r)>>1; 48 if(mid>=v){ 49 add(rt->lid,v,k,l,mid); 50 } 51 else{ 52 add(rt->rid,v,k,mid+1,r); 53 } 54 if(rt->lid!=NULL){ 55 rt->maxn = rt->lid->maxn; 56 } 57 if(rt->rid!=NULL&& 58 rt->maxn < rt->rid->maxn) 59 rt->maxn = rt->rid->maxn; 60 } 61 int dep[N],fa[N][logN],ln; 62 bool is_v[N]; 63 struct Myqu{ 64 int f,e; 65 int Q[N*10]; 66 void push(int k){ 67 e++; 68 Q[e]=k; 69 } 70 int front(){ 71 f++; 72 return Q[f]; 73 } 74 bool empty(){ 75 if(e==f)return true; 76 return false; 77 } 78 }qu; 79 void bfs(int k){ 80 qu.push(k); 81 is_v[k]=1; 82 while(!qu.empty()){ 83 int f=qu.front(); 84 for(int i=fl[f];i!=-1;i=rs[i].next){ 85 if(!is_v[rs[i].t]){ 86 qu.push(rs[i].t); 87 is_v[rs[i].t]=1; 88 fa[rs[i].t][0]=f; 89 dep[rs[i].t]=dep[f]+1; 90 for(int j=1;j<=ln;j++) fa[rs[i].t][j]=fa[fa[rs[i].t][j-1]][j-1]; 91 } 92 } 93 } 94 } 95 int lca(int a,int b){//cout<<a<<SP<<b<<endl; 96 if(dep[a]>dep[b])swap(a,b); 97 for(int i=ln;i>=0;i--) 98 if(dep[fa[b][i]]>=dep[a]){ 99 b=fa[b][i]; 100 //cout<<" "<<b<<" Dep"<<dep[b]<<endl; 101 } 102 if(a==b) return b; 103 for(int i=ln;i>=0;i--) 104 if(fa[a][i]!=fa[b][i]){ 105 a=fa[a][i],b=fa[b][i]; 106 } 107 return fa[a][0]; 108 } 109 XDS* merge(int l,int r,XDS *&a,XDS *&b){ 110 if(a==NULL)return b; 111 if(b==NULL)return a; 112 if(l==r){ 113 a->maxn =a->maxn+b->maxn; 114 delete b; 115 b=NULL; 116 return a; 117 } 118 int mid=(l+r)>>1;//puts("midgot"); 119 a->lid=merge(l,mid,a->lid,b->lid);//puts("Lid merge end"); 120 a->rid=merge(mid+1,r,a->rid,b->rid); 121 if(a->lid!=NULL){ 122 a->maxn = a->lid->maxn; 123 } 124 if(a->rid!=NULL&& 125 a->rid->maxn > a->maxn) 126 a->maxn =a->rid->maxn; 127 return a; 128 } 129 int ffind(XDS *rt,int l,int r){ 130 int mid=(l+r)>>1; 131 if(rt==NULL)return -1; 132 if(l==r)return l; 133 if(rt->lid==NULL&&rt->rid==NULL)return -1; 134 if(rt->lid==NULL)return ffind(rt->rid,mid+1,r); 135 if(rt->rid==NULL)return ffind(rt->lid,l,mid); 136 if(rt->lid->maxn>=rt->rid->maxn){ 137 return ffind(rt->lid,l,mid); 138 } 139 else return ffind(rt->rid,mid+1,r); 140 } 141 void getans(int k){ 142 is_v[k]=0; 143 for(int i=fl[k];i!=-1;i=rs[i].next){ 144 if(is_v[rs[i].t]){ 145 getans(rs[i].t); 146 root[k]=merge(1,len,root[k],root[rs[i].t]); 147 } 148 } 149 int q=ffind(root[k],1,len); 150 if(q==-1)dep[k]=0; 151 else dep[k]=val[q-1]; 152 } 153 int du[N]; 154 int main(){ 155 int a,b,c,ro; 156 memset(fl ,-1,sizeof fl); 157 scanf("%d%d",&n,&m); 158 ln=log2(n)+1; 159 for(int i=1;i<n;i++){ 160 scanf("%d%d",&a,&b); 161 add(a,b); 162 add(b,a); 163 } 164 for(int i=1;i<=m;i++){ 165 scanf("%d%d%d",&a,&b,&c); 166 q[i].x=a ,q[i].y=b ,q[i].z=val[i-1]=c; 167 du[a]++,du[b]++; 168 } 169 int maxn=-1; 170 for(int i=1;i<=n;i++){ 171 if(du[i]>maxn){ 172 ro=i; 173 maxn=du[i]; 174 } 175 } 176 sort(val+0,val+m); 177 len=unique(val,val+m)-val; 178 dep[ro]=1; 179 bfs(ro); 180 for(int i=1;i<=m;i++){ 181 int Lca=lca(q[i].x,q[i].y),val=fvind(q[i].z); 182 add(root[Lca], val,-1,1,len); 183 add(root[fa[Lca][0]],val,-1,1,len); 184 add(root[q[i].x] ,val, 1,1,len); 185 add(root[q[i].y] ,val, 1,1,len); 186 } 187 getans(ro); 188 for(int i=1;i<=n;i++){ 189 printf("%d\n",dep[i]); 190 } 191 return 0; 192 }
Miemeng真的蒻
