Index Structures
An index is any data structure that takes the value of one or more fields and finds the records with that value quickly.
Basics
Indexes can be "dense", meaning there is an entry in the index file for every record; indexes can be "sparse", meaning that only some of the data records are represented in the index, often one index entry per block of the data file.
Indexes can be "primary" and "secondary", a primary index determines the location of the records of the data file, while a secondary index does not.
Dense Indexes
If records are sorted, we can build on them a dense index. With a key K, we can use binary search to find K the index, if there are n blocks of index, we only look at \(\log_2n\) of them.
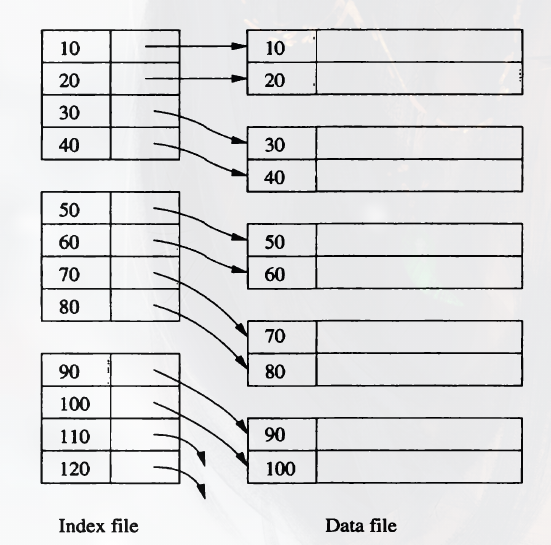
Sparse Indexes
A Sparse Index has only one key-pointer pair per block of the data file. It saves more space, but takes more time for finding a certain record.
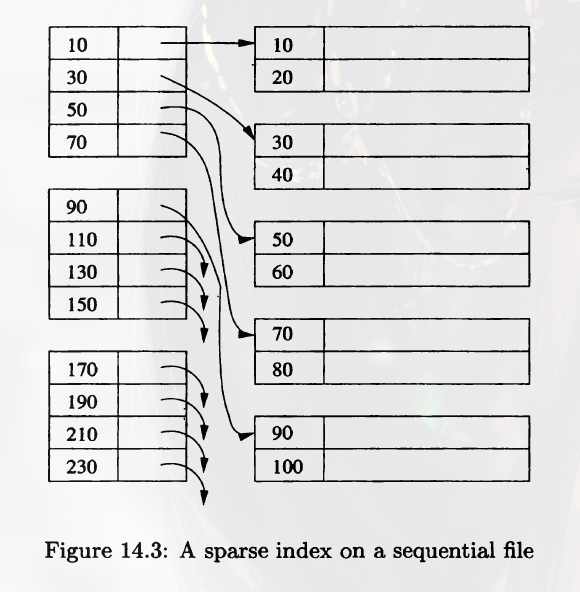
Multiple Levels of Index
An index may cover multiple blocks, so we may still need to do may disk I/O to find the correct record. So it's a good idea to build another level of index on the index, we can make the use of the first level of index more efficient.
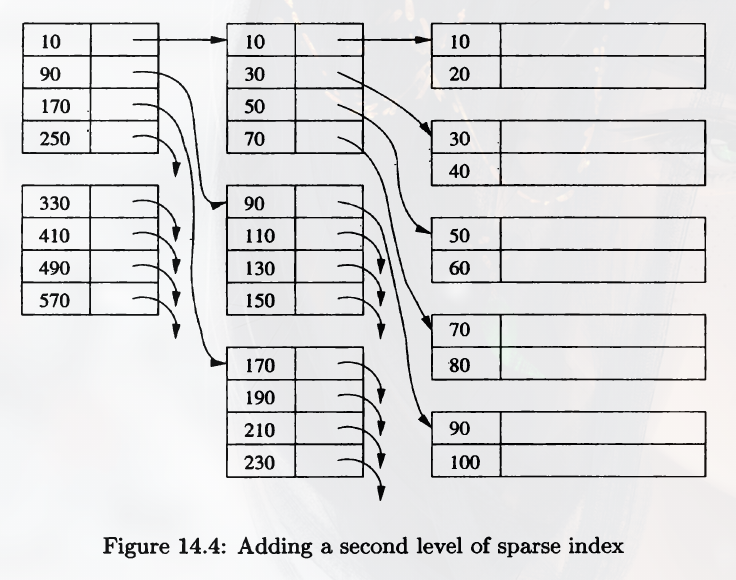
The first level indexes can be dense or sparse (sparse in the figure), however, the second level and higher must be sparse. Otherwise it would have an exact number of indexes as the first-level indexes.
When I say first-level index, I mean the level that directly points to the records, so don't get it wrong.
Secondary Indexes
A secondary index is a data structure that facilitates finding records given a value for one or more fields. However, the secondary index is distinguished from the primary index in that a secondary index does not determine the placement of records, which may have been decided by a primary index on some other field.
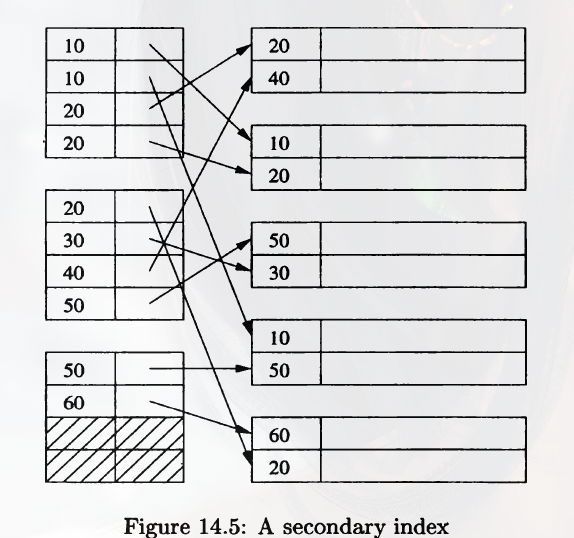
As you can see in the figure, even though all the search keys are sorted, the pointers are not sorted at all.
However, the keys in the index file are sorted, otherwise when we search with a secondary index, the DB engine has to run through all of the index-records pairs.
And most of the time, a secondary index is not unique. The result is that the pointer in one block can go to many different data blocks, instead of one or a few consecutive blocks, because normally a secondary index can match multiple records.
Thus, using a secondary index may result in many more disk I/O's than if we get the same number of records via a primary index.
Indirection in Secondary Indexes
If a search-key value appears n times in the data file, then the value is written n times in the index file.
A convenient way to avoid repeating values is to use a level of indirection, called buckets.
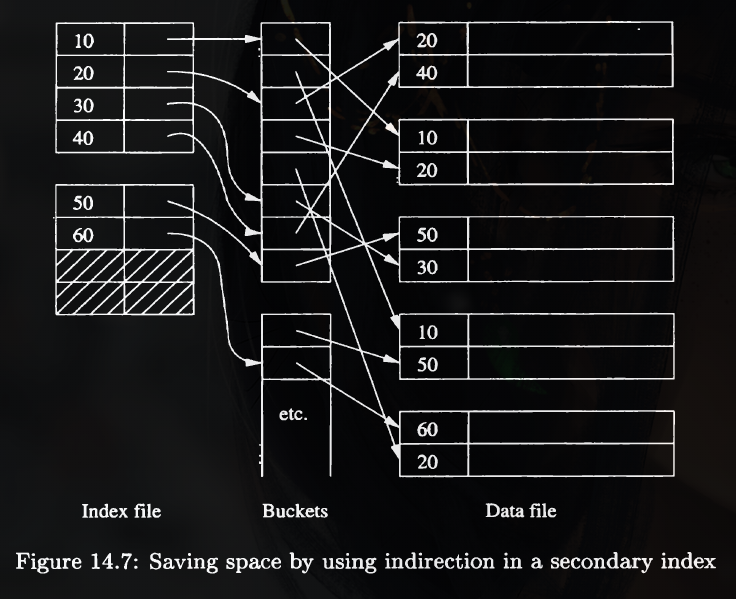
A bucket block is used to store pointers, in which pointers associated with a search value are stored consecutively.
The scheme of the figure saves space as long as search-key values are larger than pointers, and the average key appears at least twice.
However, this bucket conception has a huge defect. When we want to insert a record into the DB, as all the pointers are stored consecutively, it would cost a lot for the insert.
B-Trees
In essence:
The B+ tree is the mostly used tree in the B-Trees family.
The Structure of B-Trees
There are three layers in a B-Tree: the root, an intermediate layer, and leaves, but any number of layers is possible.
There is a parameter \(n\) associated with each B-Tree index, and this parameter determines the layout of all blocks of the B-Tree. Each block will have space for \(n\) search-key and \(n+1\) pointers.
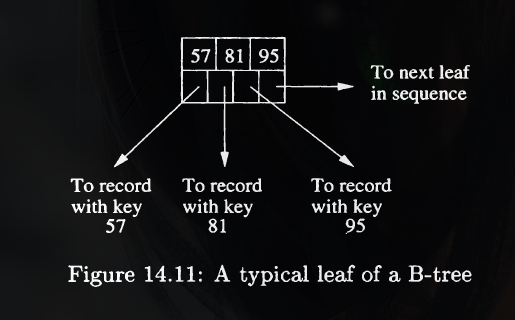
Several rules in a B-Tree:
If $j$ pointers are used, then there will be $j-1$ keys, say $K_1,K_2,\cdots, K_{j-1}$. The first pointer points to a part of the B-tree where some of the records with keys less than $K_1$ will be found. The second pointer goes to that part of the tree where all records with keys that are at least $K_1$, but less than $K_2$ will be found, and so on.
Note that some records with keys fat below $K_1$ or fat above $K_{j-1}$ may not be reachable from this block at all, but will be reached via another block at the same level.
