线性系统的时域分析方法

第三章 线性系统的时域分析方法

3-1 系统时间响应的性能指标

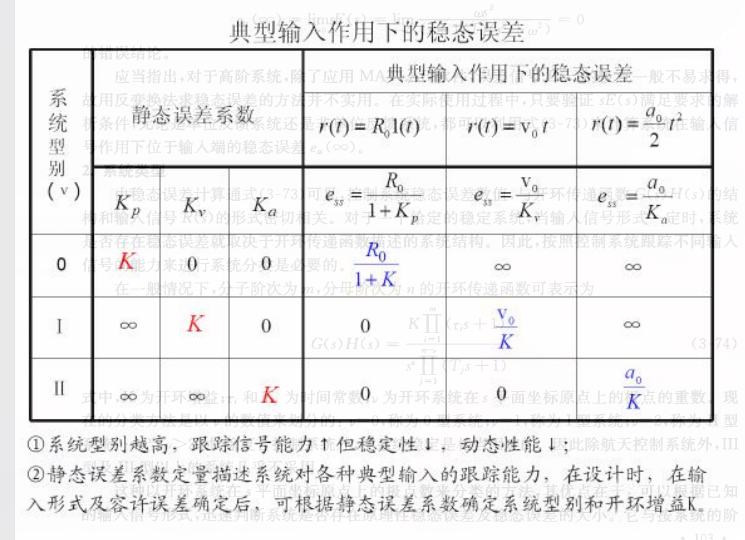
1. 典型输入信号

2. 动态过程与稳态过程

动态过程：指系统在典型输入信号下，系统输出量从初始状态到最终状态的响应过程。根据系统结构和参数选择情况，动态过程表现为衰减、发散或等幅振荡形式。

稳态过程：系统在典型输入信号下，当时间t趋向于无穷时，系统输出量的表现形式。

3. 动态性能

1. 上升时间：响应从终值10%上升到90%所需的时间；对于有振荡的系统，亦定义为响应从零第一次上升到终值所需要的时间。上升时间越短，响应速度越快。
2. 峰值时间：响应超过其终值到达第一个峰值所需的时间
3. 调节时间：响应到达并保持在终值 $\pm$5% 内所需的最短时间
4. 超调量 $\sigma\%$：响应的最大偏离量 $c(t_p)$ 与终值 $c(\infty)$ 的差与终值 $c(\infty)$ 比的百分数。若 $c(t_p)<c(\infty)$，则响应无超调。

3-2 一阶系统的时域分析

系统对输入信号导数的响应，等于系统对于输入信号响应的导数。

跟踪能力：

时间常数越小，响应速度u越快。

阶跃输入：无稳态误差；斜坡输入：稳态误差等于时间常数T

当传递函数为 $\Phi(s) = \frac1{Ts+1}$时，一阶系统对典型输入信号的输出响应：

输入信号	输出响应
$1(t)$	$1-e^{-t/T},\quad t\ge0$
$\delta(t)$	$\frac1Te^{-t/T}\quad t\ge0$
$t$	$t-T+Te^{-t/T}\quad t\ge0$
$\frac12t^2$	$\frac12t^2-Tt+T^2(1-e^{-t/T})\quad t\ge 0$

3-3 二阶系统的时域分析

标准二阶系统微分方程

$$\ddot{c}(t)+2\zeta\omega_n\dot c(t) + \omega_n^2c(t) = \omega_n^2r(t)$$

闭环传递函数

$$\Phi(s) = \frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}$$

$\omega_n$ —— 无阻尼自然振荡频率

$\zeta$ ——阻尼比（相对阻尼系数）

开环传递函数

$$G(s) = \frac{\omega_n^2}{s(s+2\zeta\omega_n)}$$

标准二阶系统的特征方程和特征根

令闭环传递函数的分母等于0就得到了标准二阶系统的特征方程

$$s^2+2\zeta\omega_ns+\omega_n^2=0 \\s_{1,2} = -\zeta\omega_n\pm\omega_n\sqrt{\zeta^2-1}$$

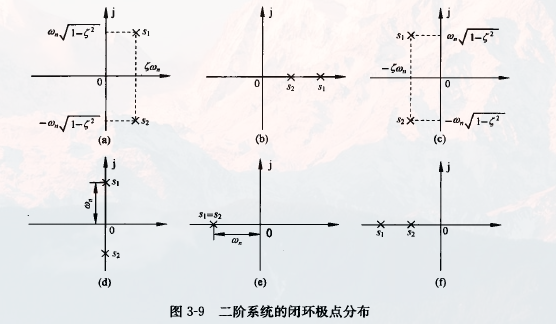
$\zeta$ 的取值决定特征根在 $s$ 平面的位置。

称：

$0<\zeta<1$ —— 欠阻尼

$\zeta = 1$ —— 临界阻尼

$\zeta > 1$ —— 过阻尼

$\zeta = 0$ —— 无阻尼

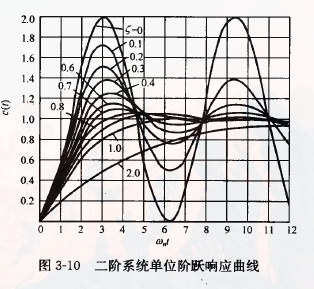
二阶系统单位阶跃响应

1. 欠阻尼的单位阶跃响应

$$C(s) = \frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}\cdot\frac1s\\ c(t) = 1-\frac1{\sqrt{1-\zeta^2}}e^{-\zeta\omega_nt}\sin(\omega_nt+\theta)$$

其中

$$\theta = \arccos\zeta$$

是一个稳态值为1的振荡衰减过程。

2. 无阻尼

$$h(t) = 1-\cos\omega_nt\quad t\ge0$$

为一个等幅振荡过程。

3. 临界阻尼

$$c(t) = 1-e^{-\omega_nt}(1+\omega_nt)\quad t\ge 0$$

4. 过阻尼

$$c(t) = 1+\frac{e^{-t/T_1}}{T_2/T_1-1}+\frac{e^{-t/T_2}}{T_1/T_2-1}\quad t\ge0\\ T_1=\frac1{\omega_n(\zeta-\sqrt{\zeta^2-1})}\\ T_2=\frac1{\omega_n(\zeta+\sqrt{\zeta^2-1})}$$

欠阻尼二阶系统的性能分析

上升时间 $t_r$

令 $h(t) =1$得

$$t_r = \frac{\pi-\theta}{\omega_n\sqrt{1-\zeta^2}}$$

其中 $\omega_d=\omega_n\sqrt{1-\zeta^2}$ 被称为阻尼振荡频率。

$\theta = \arccos\zeta$ 称为阻尼角。

峰值时间 $t_p$

令 $\frac{\mathrm dh(t)}{\mathrm dt} = 0$得

$$t_p = \frac\pi{\omega_n\sqrt{1-\zeta^2}}$$

超调量

$$\sigma_p = e^{-\pi\zeta/\sqrt{1-\zeta^2}}\times100\%$$

调节时间（从振荡开始到回归到一定误差范围内的正常值）

$$t_s = \frac3{\zeta\omega_n}(5\%的误差带)\\ t_s = \frac4{\zeta\omega_n}(2\%的误差带)$$

延迟时间

$$t_d = \frac{1+0.7\zeta}{\omega_n}$$

振荡次数

$$N = \frac{t_s\omega_d}{2\pi}$$

过阻尼系统的性能分析

上升时间

$$t_r =\frac{1+1.5\zeta+\zeta^2}{\omega_n}$$

高阶系统的时域分析

当已知高阶系统的各个闭环极点后，可以将其化为以下形式：

$$\Phi(s) = \sum_{j=1}^q\frac{A_j}{s+s_j}+\sum_{k=1}^r\frac{B_ks+c_k}{s^2+2\zeta_k\omega_{nk}s+\omega_{nk}^2}$$

实部为负的极点

越靠近虚轴，衰减速度越慢，对过渡过程的影响越大。

闭环极点约靠近虚轴，超调量越大；

二阶系统的单位斜坡响应

欠阻尼

$$c(t) = t-\frac{2\zeta}{\omega_n}+\frac1{\omega_n\sqrt{1-\zeta^2}}e^{-\zeta\omega_nt}\sin(\omega_nt\sqrt{1-\zeta^2}+2\arccos\zeta)$$

临界阻尼

$$c(t) = t-\frac2{\omega_n}+\frac2{\omega_n}(1+\frac12\omega_nt)e^{-\omega_nt}\quad t\ge0$$

过阻尼

$$\begin{aligned} c(t) = t-\frac{2\zeta}{\omega_n}&+\frac{2\zeta^2-1+2\zeta\sqrt{\zeta^2-1}}{2\omega_n\sqrt{1-\zeta^2}}e^{-(\zeta-\sqrt{\zeta^2-1})\omega_nt}\\ &-\frac{2\zeta^2-1-2\zeta\sqrt{\zeta^2-1}}{2\omega_n\sqrt{1-\zeta^2}}e^{-(\zeta+\sqrt{\zeta^2-1})\omega_nt} \end{aligned}$$

稳态分量恒为 $t-\frac{2\zeta}{\omega_n}$

二阶系统性能改善

（1）比例-微分控制

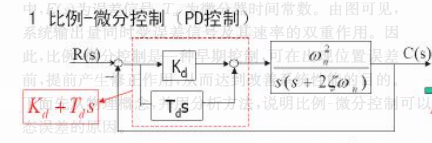
则闭环传递函数变为

$$\Phi(s) = \frac{(T_ds+K_d)\omega_n^2}{s^2+(2\zeta\omega_n+T_d\omega_n^2)s+\omega_n^2}$$

使用比例-微分控制后，既可以减小系统在斜坡输入时的稳态误差，又可以使系统在阶跃输入时有满意的动态性能。

（2）测速反馈控制

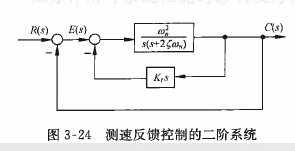
通过将输出的速度信号反馈到输入端，并与误差信号比较，可以增大系统阻尼，改善系统性能。

与微分-控制系统不同的是，测速反馈会降低系统的开环增益，从而加大系统在斜坡输入时的稳态误差。

3-5 线性系统的稳定性分析

稳定性是指系统在受到扰动下偏离原始状态，在扰动消失后恢复到原平衡状态的性能。

如果系统受到扰动后，无论初始偏差有多大，都能恢复到原始平衡状态，则这种系统称为大范围稳定的系统；如果初始偏差只在小于某一范围时才能恢复到初始平衡状态，则称这种系统为小范围平衡的系统。

稳定的充要条件

当且仅当系统的特征根全部具有负实部时，系统才具有稳定性；若有一个正实部根，不稳定；若有一个或一个以上零实部，则具有临界稳定性。

赫尔韦斯判定

劳斯判定

劳斯表的计算：对于上面的那个四元素矩阵：负对角线减去主对角线除以左下角的值。

劳斯判定的特殊情况

1. 劳斯表中的某行的第一列项为零，而其余各项不为零，或不全为零

   可以用因子 $(s+a)$ 乘以原特征方程，其中 $a$ 为任意正数。

2. 劳斯表中出现全零行

   根据上一行的系数构建一个辅助方程，求导后作为系数写入。

3-6 线性系统的稳态误差计算

$$E(s) = R(s) - H(s)C(s)$$

误差的時域表达式为

$$e(t) = \mathcal{L}^{-1}[E(s)] = \mathcal{L}^{-1}[\Phi(s)R(s)]$$

如果 $sE(s)$ 的极点均位于 $s$ 左半平面（包括坐标原点），根据拉氏变换的终值定理，可方便地求出稳态误差

$$e_{ss}(\infty) = \lim_{s\rightarrow0}sE(s) = \lim_{s\rightarrow0}\frac{sR(s)}{1+G(s)H(s)}$$

这里要注意拉普拉斯变换终值定理的应用条件：$sE(s)$ 的全部极点位于 $s$ 平面的左半平面。

系统类型

在一般情况下，分子阶次为 m, 分母阶次为 n的开环传递函数为

$$G(s)H(s) = \frac{K\prod_{i=1}^m(\tau_Is+1)}{s^v\prod_{j=1}^{n-v}(T_{jS}+1)}$$

其中 $K$ 为开环增益

我们通过 $v$ 的数值来称呼相应系统的类型，比如 $v = 0$ 就是零型系统，$v=1$就是I型系统。

3-7 扰动作用下的稳态误差

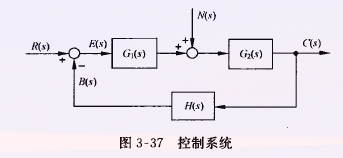
如图为有扰动作用下的信号流图

令输入 $R(s)=0$，得扰动的传递函数

$$\Phi_n(s) = -\frac{G_2}{1+G_1G_2H}$$

扰动输入的稳态误差

$$e_{nss} = \lim_{s\rightarrow0}s\cdot E_n(s)=\lim_{s\rightarrow0}s\cdot\Phi_n(s)\cdot N(s)$$