[算法学习]斐波那契数的计算

决定开始看algorithms，而且尽量多思考，多写点代码。第一个碰到的算法就很具有启发性，一些看似正确的算法，实际的复杂度却很高。我们直接看问题：

---

问题：假设fibonacci(0)=0,fibonacci(1)=1,如果计算fibonacci(n)

解决方案一：直接利用斐波那契数的性质用递归计算

 def fibonacci1(n):
2     if n == 0:
3         return 0
4     elif n == 1:
5         return 1
6     else:
7         return fibonacci1(n-1)+fibonacci1(n-2)

一看好像这样做没什么不妥，但是你如果跑下fibonacci1(50)机器就开始忙碌了，仔细想想，这个算法的复杂度其实是O(2ⁿ),看看原书上的图就明白了

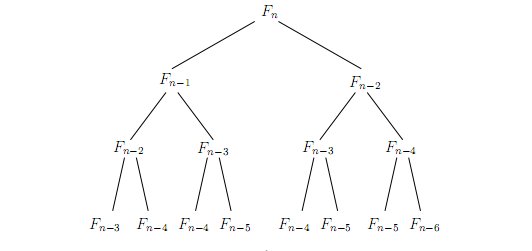
其中重复的计算很多，最后需要计算的次数是2^0.694n +3n次，这个明显是不行的，当n较大时，什么电脑都要跑上很久很久

解决方案二：不用递归，直接用循环计算

 def fibonacci2(n):
2     fib=[0, 1]
3     for i in range(2,n+1):
4         fib.append(fib[i-1]+fib[i-2])
5     return fib[n]

这种做法也比较直观，很明显这种方法的复杂度是O(n)。一般来说，你肯定会觉得这样就够了，实际上还有logn复杂度的方法。

解决方案三：用矩阵计算

斐波那契数的性质可以用矩阵来表示：，那么有。我们用X来表示其中的0111矩阵，那么对于Fn，我们只要计算Xⁿ

就可以得到Fn。当然我们不能用循环来计算Xⁿ ，而是用“折半法“通过X^n/2 *X^n/2计算。

 1 def fibonacci3(n):
 2     return recuCal(n)[1]
 3 
 4 matrix=[0,1,1,1]
 5 def recuCal(n):
 6     if n == 1:
 7         return matrix
 8     elif n == 2:
 9         return matrixCal(matrix,matrix)
10     elif n % 2:
11         return matrixCal(matrixCal(recuCal(n/2),recuCal(n/2)),matrix)
12     else:
13         return matrixCal(recuCal(n/2),recuCal(n/2))
14 
15 def matrixCal(matrix1,matrix2):
16     matrix3 = [0,0,0,0]
17     matrix3[0]=matrix1[0]*matrix2[0]+matrix1[1]*matrix2[2]
18     matrix3[1]=matrix1[0]*matrix2[1]+matrix1[1]*matrix2[3]
19     matrix3[2]=matrix1[2]*matrix2[0]+matrix1[3]*matrix2[2]
20     matrix3[3]=matrix1[2]*matrix2[1]+matrix1[3]*matrix2[3]
21     return matrix3

算法比较简单，matrixCal是计算两个矩阵的方法。recuCal是实现“折半法”的函数，返回计算结果矩阵，而这个矩阵的第2个数就是需要的结果。

---

以上代码都是用python写的，可以再写一个main来验证结果：

 if __name__ == '__main__':
2     print fibonacci1(50)
3     print fibonacci2(50)
4     print fibonacci3(50)

当然fibonacci1(50)短时间跑不完的。最好还是把n定小点。

写完咯，睡觉