【Python】【demo实验7】【练习实例】【完全平方数相关】
题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
程序分析:可填在百位、十位、个位的数字都是1、2、3、4。组成所有的排列后再去 掉不满足条件的排列。
假设该数为 x。
1、则:x + 100 = n2, x + 100 + 168 = m2
2、计算等式:m2 - n2 = (m + n)(m - n) = 168
3、设置: m + n = i,m - n = j,i * j =168,i 和 j 至少一个是偶数
4、可得: m = (i + j) / 2, n = (i - j) / 2,i 和 j 要么都是偶数,要么都是奇数。
5、从 3 和 4 推导可知道,i 与 j 均是大于等于 2 的偶数。
6、由于 i * j = 168, j>=2,则 1 < i < 168 / 2 + 1。
7、接下来将 i 的所有数字循环计算即可。
程序源代码(原为Python2.0):
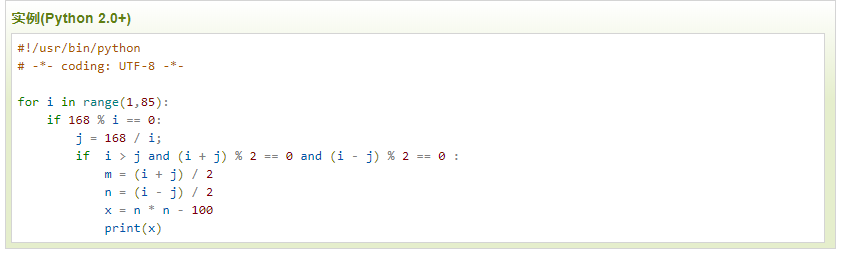
这个计算方法挺有意思,待研究

我的源代码:
#!/usr/bin/python # encoding=utf-8 # -*- coding: UTF-8 -*- # 题目:一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少? # 解题思路:先找出这个数的大概范围z # 在通过定义的函数判断各个数是否为完全平方数,是否符合题目条件; #验证是否为完全平方数 import math def isSqr(n): a = int((math.sqrt(n))) return a * a == n #自定义函数的返回值,对于完全平方数,返回True,非完全平方数返回False; #通过这个循环判断答案的边界,为下一个循环输入参数; #随着因数t的增加,其平方与t+1的平方之差会越来越多,所以通过这个规律设置这个循环 #题目中两个完全平方数之差为168 for y in range(0,10000): if (y+1)**2-y**2>=168: z=y**2+1 #range迭代时,不包含第二个参数 print("y:",y,"z:",z) break #最小数值应从-100开始 for i in range(-100,z): if i%10 in [0,1,4,5,6,9]: #根据完全平方数的特性,个位数只能是这几个数。 if isSqr(i+100) and isSqr(i+268): print(i,"##",(i+100)**0.5,"&&&",(i+268)**0.5)
输出结果:
C:\Python30_demo>python 018demo.py y: 84 z: 7057 -99 ## 1.0 &&& 13.0 21 ## 11.0 &&& 17.0 261 ## 19.0 &&& 23.0 1581 ## 41.0 &&& 43.0
总共有四个数字,-99,1,21,261,1581
————————(我是分割线)————————
参考:
1. RUNOOB.COM : https://www.runoob.com/python/python-exercise-example3.html
2. https://www.cnblogs.com/zlsjjn/p/7459607.html
3. 百度百科:https://baike.baidu.com/item/%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0/8025061?fr=aladdin
备注:
初次编辑时间:2019年9月22日23:37:37
第一次修改:2019年9月23日00:06:08 / 修改格式及部分重复内容
环境:Windows 7 / Python 3.7.2


