P4381 [IOI2008]Island（基环树+单调队列优化dp）

P4381 [IOI2008]Island

题意：求图中所有基环树的直径和

我们对每棵基环树分别计算答案。

首先我们先bfs找环（dfs易爆栈）

蓝后我们处理直径

直径不在环上，就在环上某点的子树上

我们对于环上每个点的子树，跑一边dp求直径即可，顺带处理子树的最深深度（环上点到子树某个叶节点的最长距离）$dis[x]$

在dfs求直径时顺带求直径的最大值（可能是整棵基环树的直径）

蓝后我们在环上跑一遍dp。

我们先破环成链（就是把长度为$n$的环转换成长$2n+1$的链）

偷个图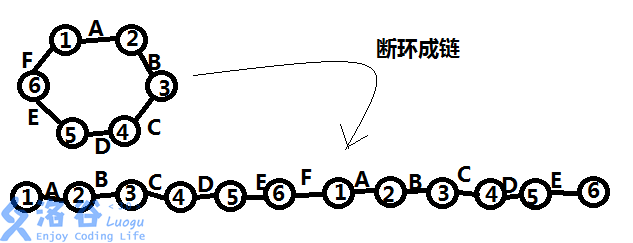

 

我们记链上前$i$个点之间边的总长（前缀和）$sum[i]$

枚举$j(1<=j<i,i-j<n)$，得

$ans=max(ans,dis[i]+sum[i]-sum[j]+dis[j])$，表示子树$i$的直径$+$子树$j$的直径+$i,j$在环上之间的距离

我们分离一下上面的式子：$(dis[i]+sum[i])+(dis[j]-sum[j])$

这不是可以单调队列维护

于是再搞个单调队列优化dp就完事辣

bzoj还是爆栈了TAT

#include<iostream>
#include<cstdio>
#include<cstring>
#define rint register int
using namespace std;
typedef long long ll;
inline ll Max(ll a,ll b){return a>b?a:b;}
void read(int &x){
    char c=getchar();x=0;
    while(c<'0'||c>'9') c=getchar();
    while('0'<=c&&c<='9') x=x*10+(c^48),c=getchar();
}
#define N 1000005
int n,ri[N],d[N],is[N],To[N],W[N],fa[N],len,L,R,h[N]; 
ll ans,re,sum[N],dis[N]; bool vis[N];
int cnt,hd[N],nxt[N<<1],ed[N],poi[N<<1],val[N<<1];
inline void adde(int x,int y,int v){
    nxt[ed[x]]=++cnt, hd[x]=hd[x]?hd[x]:cnt;
    ed[x]=cnt, poi[cnt]=y, val[cnt]=v;
}
void bfs(int x){//找环
    rint p; vis[x]=1;len=0;
    while(1){
        p=To[x];
        if(vis[p]){
            ri[++len]=p,d[len]=W[p],is[p]=1;
            for(;x!=p;x=fa[x])
                ri[++len]=x,d[len]=W[x],is[x]=1;
            break;
        }vis[p]=1;fa[p]=x;x=p;
    }
}
void dfs(int x,int Fa){//dfs求子树直径
    vis[x]=1;
    for(int i=hd[x];i;i=nxt[i]){
        int to=poi[i];
        if(is[to]||to==Fa) continue;
        dfs(to,x); re=Max(re,dis[x]+dis[to]+(ll)val[i]);
        dis[x]=Max(dis[x],dis[to]+val[i]);
    }
}
inline int Id(int x){return (x-1)%len+1;}
inline ll F(int x){return dis[ri[Id(x)]]-sum[x];}
void solve(){//单调队列优化，环上dp
    L=1;R=0;
    for(rint i=1;i<=len*2;++i){
        sum[i]=sum[i-1]+d[Id(i)];
        while(L<=R&&i-h[L]>=len) ++L;
        if(L<=R) re=Max(re,F(h[L])+dis[ri[Id(i)]]+sum[i]);
        while(L<=R&&F(h[R])<=F(i)) --R;
        h[++R]=i;
    }
}
int main(){
    read(n);
    for(rint i=1;i<=n;++i){
        read(To[i]); read(W[i]);
        adde(i,To[i],W[i]); adde(To[i],i,W[i]);
    }
    for(rint i=1;i<=n;++i){
        if(vis[i]) continue;
        re=0; bfs(i);
        for(rint j=1;j<=len;++j) dfs(ri[j],0);
        solve(); ans+=re;//每棵树分别处理
    }printf("%lld",ans);
    return 0;
}